Four ways of solving three pressurized thick cylinders
| Title | Four ways of solving three pressurized thick cylinders |
| Tags | elasticity plane-stress |
| Runnng time | 30 secs |
| CAEplex case | https://caeplex.com/p/41dd1 |
| Available in | HTML PDF ePub |
1 Problem description
Let’s consider a thick axisymmetric membrane cylinder depicted in fig. 1 which is governed by the Lamé equations
\sigma_r(r) = a - \frac{b}{r^2}
\sigma_h(r) = a + \frac{b}{r^2}
u_r(r) = \frac{r}{E} \Big[ \sigma_h(r) - \nu \cdot \sigma_r(r) \Big]
which give the radial stress \sigma_r, the hoop stress \sigma_h and the radial displacement u as a function of the radius r for plane-stress constitutive equations with Young modulus E and Poisson’s ratio \nu. The coefficients a and b are determined from the pressure boundary conditions of the problem p_i and p_o, set at the inner and outer radii r_i and r_o respectively. These equations do not consider body and thermal loading terms.
This case file uses four methods, namely
- The continuous Lamé equations
- 2D plane-stress finite elements
- 2D axi-symmetric elements
- 3D finite elements
to solve these three geometries and boundary conditions
| Case | r_i [mm] | r_o [mm] | p_i [MPa] | p_o [MPa] | a [MPa] | b [kN] |
|---|---|---|---|---|---|---|
| A | 100.0 | 1000 | 0.1 | 0.1 | 0.1 | 0 |
| B | 100.0 | 1000 | -10 | -0.1 | 0 | 100 |
| C | 140.4 | 161.9 | -10 | -1.0 | 26.3 | 715.474 |
These considerations are taken into account:
One of the objectives of this case file is to evaluate how the errors commited by finite-elements formulations with respect to the Lamé equations depend on the number of elements used in the cylinder thickness. No attention is payed to the total number of degrees of freedom involved in each method whatsoever.
The base computations are performed using 16 second-order tensor-product elements through the cylinder width. A parametric study with respect to the number of elements is performed afterwards.
For the plane-stress and the full 3D cases a symmetry of one quarter is used so exact Dirichlet boundary conditions can be used. Any symmetry angle smaller than 90º would require a multi-freedom boundary condition, which in Fino are implemented as a penalty method so they cannot be enforced exactly.
For the axi-symmetric and the full 3D cases the height of the cylinder is equal to 10% of the radii average (r_i+r_o)/2 and is meshed using one quarter of the number of elements used for the thickness (i.e. four elements).
2 Geometry and meshes
The three FEM cases use a Gmsh .geo script file to create the geometry and the base mesh with 16 elements through the thickness. Fig. 2 and fig. 3 show the resulting grids for each case (A and B have the same geometry and mesh).
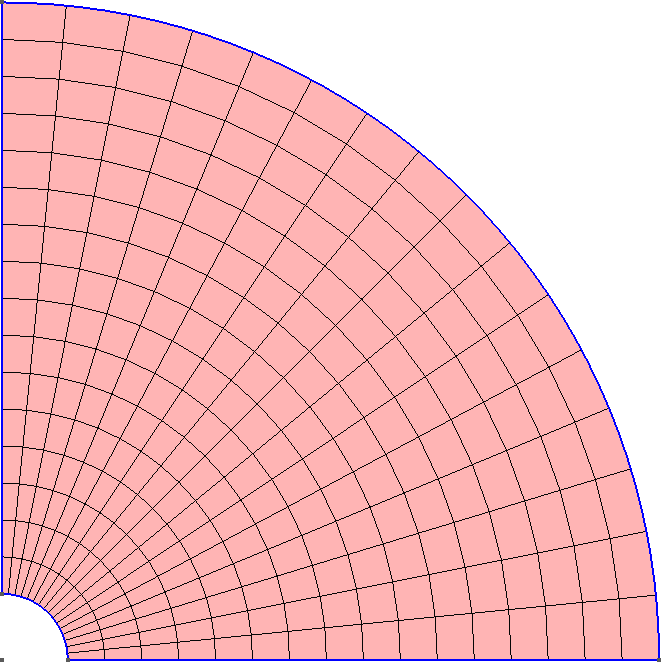

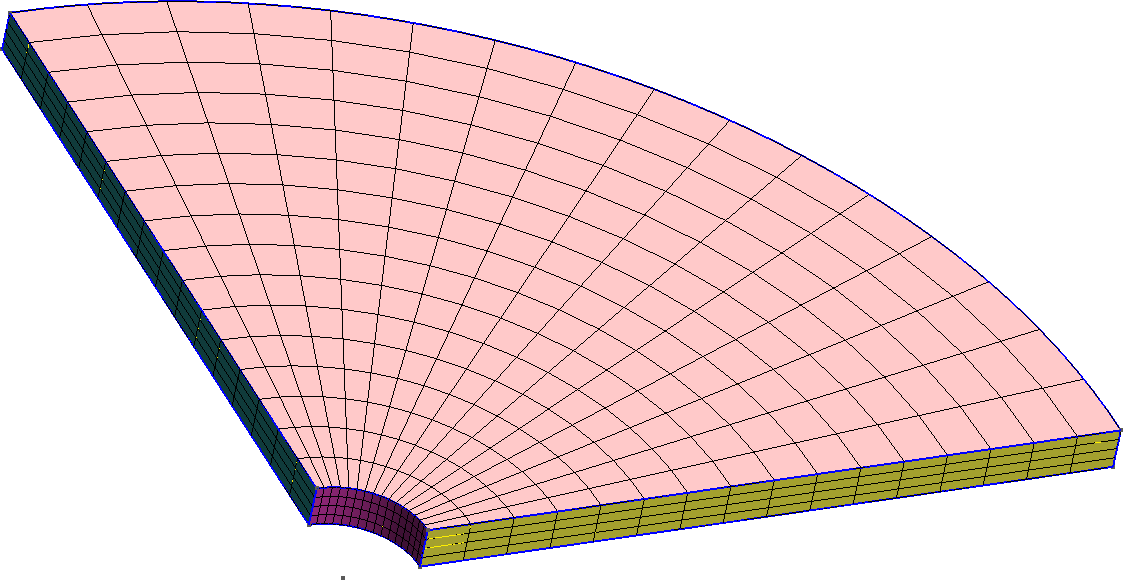
Figure 2: Three FEM meshes for cases A & B. a — Plane-stress, b — Axially symmetric, c — Three dimensional



Figure 3: Three FEM meshes for case C. a — Plane-stress, b — Axially symmetric, c — Three dimensional
Each case A, B and C has a file caseX.fin that defines the geometric parameters from the table above as scalar variables. These three files can be read both by Gmsh and Fino, provided the lines are finished with a colon ; (otherwise Gmsh would complain):
Now there exist three Gmsh geometry scripts that read the per-case definitions above and create the three FEM meshes. The plane stress case is created by plane.geo, the axially-symmetric case with axi.geo and the three dimensional one with full.geo:
SetFactory("OpenCASCADE");
Point(1) = {0, 0, 0};
Point(2) = {r_i, 0, 0};
Point(3) = {r_o, 0, 0};
Point(4) = {0, r_i, 0};
Point(5) = {0, r_o, 0};
Line(1) = {2, 3};
Line(2) = {5, 4};
Circle(3) = {3, 1, 5};
Circle(4) = {4, 1, 2};
Curve Loop(1) = {1, 3, 2, 4};
Plane Surface(1) = {1};
Transfinite Line {1:2} = n+1;
Transfinite Line {3:4} = n+1;
Transfinite Surface {1};
Mesh.RecombineAll = 1;
Mesh.ElementOrder = 2;
Physical Curve("inner") = {4};
Physical Curve("outer") = {3};
Physical Curve("bottom") = {1};
Physical Curve("left") = {2};
Physical Surface("bulk") = {1};SetFactory("OpenCASCADE");
Rectangle(1) = {r_i, -0.05*0.5*(r_i+r_o), 0, r_o-r_i, 0.1*0.5*(r_i+r_o)};
Point(5) = {0, 0, 0};
Physical Curve("inner") = {4};
Physical Curve("outer") = {2};
Physical Curve("bottom") = {1};
Physical Curve("top") = {3};
Physical Surface("bulk") = {1};
Transfinite Line {1,3} = n+1;
Transfinite Line {2,4} = n/4+1;
Transfinite Surface {1};
Mesh.RecombineAll = 1;
Mesh.ElementOrder = 2;SetFactory("OpenCASCADE");
Point(1) = {0, 0, 0};
Point(2) = {r_i, 0, 0};
Point(3) = {r_o, 0, 0};
Point(4) = {0, r_i, 0};
Point(5) = {0, r_o, 0};
Line(1) = {2, 3};
Line(2) = {5, 4};
Circle(3) = {3, 1, 5};
Circle(4) = {4, 1, 2};
Curve Loop(1) = {1, 3, 2, 4};
Plane Surface(1) = {1};
Transfinite Line {1:2} = n+1;
Transfinite Line {3:4} = n+1;
Transfinite Surface {1};
Mesh.RecombineAll = 1;
Mesh.ElementOrder = 2;
Extrude {0, 0, 0.1*0.5*(r_i+r_o)} {
Surface{1}; Layers{n/4}; Recombine;
}
Physical Surface("inner") = {5};
Physical Surface("outer") = {3};
Physical Surface("bottom") = {2};
Physical Surface("left") = {4};
Physical Surface("infinite") = {1,6};
Physical Volume("bulk") = {1};So all the meshes can be created with two nested Bash loops as
#!/bin/bash
declare -A dim=([plane]=2 [axi]=2 [full]=3)
for j in plane axi full; do
for i in A B C; do
gmsh -${dim[${j}]} case${i}.fin ${j}.geo -o ${j}${i}.msh
done
done3 Input files
Very much like in the previous section, there are now four Fino input files that solve the three cases in four different ways. The first one in not a finite-element problem but a purely algebraic problem. As Fino works on wasora, it can handle them perfectly well. The four .fin files take an extra command-line argument which should be either A, B or C. They all write the following seven columns
- r
- u_r(r)
- \sigma_r(r)
- \sigma_h(r)
- \left| \text{Lam\'e's}~u_r(r)-u_r(r)\right| / \left| \text{Lam\'e's}~u_r(r) \right|
- \left| \text{Lam\'e's}~\sigma_r(r)-\sigma_r(r))\right| / \left| \text{Lam\'e's}~\sigma_r(r) \right|
- \left| \text{Lam\'e's}~\sigma_h(r)-\sigma_h(r))\right| / \left| \text{Lam\'e's}~\sigma_h(r) \right|
for the range r \in [r_i, r_o] with intervals \Delta r = (r_o-r_i)/(8 \cdot 16) so all the functions of r are actually evaluated at the nodes but also interpolated at eight locations inside each element.
Each of the four input files lame.fin, axi.fin, plane.fin and full.fin includes the two common files properties.fin and analytical.fin.
MESH FILE_PATH axi$1.msh DIMENSIONS 2
FINO_PROBLEM mechanical axisymmetric SYMMETRY_AXIS y
# FINO_SOLVER KSP_TYPE mumps
INCLUDE properties.fin
INCLUDE case$1.fin
PHYSICAL_GROUP inner BC p=p_i
PHYSICAL_GROUP outer BC p=p_o
FINO_STEP
INCLUDE analytical.fin
sigma_r_axi(r) := sigmax(r,0)
sigma_h_axi(r) := E/((1+nu)*(1-2*nu))*(nu*dudx(r,0) + nu*dvdy(r,0) + (1-nu)*u(r,0)/r)
u_axi(r) := u(r,0)
MESH_POST FILE_PATH axi$1.vtk VECTOR u v 0 sigma1 sigma2 sigma3
PRINT_FUNCTION FORMAT %e {
u_axi sigma_r_axi sigma_h_axi
(u_axi(r)-u_r(r))/u_r(r)
abs(sigma_r_axi(r)-sigma_r(r))/abs(sigma_r(r))
abs(sigma_h_axi(r)-sigma_h(r))/abs(sigma_h(r))
\MIN r_i MAX r_o STEP (r_o-r_i)/(8*n) }MESH FILE_PATH plane$1.msh DIMENSIONS 2
FINO_PROBLEM mechanical plane_stress
# FINO_SOLVER KSP_TYPE mumps
INCLUDE properties.fin
INCLUDE case$1.fin
PHYSICAL_GROUP left BC u=0
PHYSICAL_GROUP bottom BC v=0
PHYSICAL_GROUP inner BC p=p_i
PHYSICAL_GROUP outer BC p=p_o
FINO_STEP
INCLUDE analytical.fin
sigma_r_plane(r) := sigmax(r,0)
sigma_h_plane(r) := sigmay(r,0)
u_plane(r) := u(r,0)
MESH_POST FILE_PATH plane$1.vtk VECTOR u v 0 sigma1 sigma2 sigma3
PRINT_FUNCTION FORMAT %e {
u_plane sigma_r_plane sigma_h_plane
(u_plane(r)-u_r(r))/u_r(r)
abs(sigma_r_plane(r)-sigma_r(r))/abs(sigma_r(r))
abs(sigma_h_plane(r)-sigma_h(r))/abs(sigma_h(r))
\MIN r_i MAX r_o STEP (r_o-r_i)/(8*n)}MESH FILE_PATH full$1.msh DIMENSIONS 3
FINO_PROBLEM mechanical
# FINO_SOLVER KSP_TYPE mumps
INCLUDE properties.fin
INCLUDE case$1.fin
PHYSICAL_GROUP left BC u=0
PHYSICAL_GROUP bottom BC v=0
# PHYSICAL_GROUP infinite BC w=0
PHYSICAL_GROUP inner BC p=p_i
PHYSICAL_GROUP outer BC p=p_o
FINO_STEP
INCLUDE analytical.fin
sigma_r_full(r) := sigmax(r,0,0)
sigma_h_full(r) := sigmay(r,0,0)
u_full(r) := u(r,0,0)
MESH_POST FILE_PATH full$1.vtk VECTOR u v w sigma1 sigma2 sigma3
PRINT_FUNCTION FORMAT %e {
u_full sigma_r_full sigma_h_full
(u_full(r)-u_r(r))/u_r(r)
abs(sigma_r_full(r)-sigma_r(r))/abs(sigma_r(r))
abs(sigma_h_full(r)-sigma_h(r))/abs(sigma_h(r))
\MIN r_i MAX r_o STEP (r_o-r_i)/(8*n)}4 Execution
The meshes and the cases can be solved all at once with a Bash script. Also the results can be plotted with Pyxplot in the same loop as well.
#!/bin/bash
declare -A dim=([lame]=2 [plane]=2 [axi]=2 [full]=3)
for j in lame plane axi full; do
for i in A B C; do
if [ -e ${j}.geo ]; then
if [ ! -e ${j}${i}.msh ]; then
gmsh -${dim[${j}]} case${i}.fin ${j}.geo -o ${j}${i}.msh
fi
fi
echo solving ${j} ${i}
fino ${j}.fin ${i} > ${j}${i}.dat
m4 -Dxxx=${j}${i} plot.ppl.m4 | pyxplot
pdf2svg ${j}${i}.pdf ${j}${i}.svg
pdf2svg error-${j}${i}.pdf error-${j}${i}.svg
done
done
for i in A B C; do
m4 -Dxxx=${i} compare.ppl.m4 | pyxplot
done$ ./run.sh
solving lame A
solving lame B
solving lame C
solving plane A
solving plane B
solving plane C
solving axi A
solving axi B
solving axi C
solving full A
solving full B
solving full C
$5 Results
Figs. 4-6 show the displacements, radial and hoop stresses for each of the three cases solved with the four methods in the same plot. All the solutions seem to coincide, but figs. 7-9 show the relative error of each method with respect to the Lamé equations.
Figure 4: Results for case A. a — Displacements for case A, b — Radial stress for case A, c — Hoop stress for case A
Figure 5: Results for case B. a — Displacements for case B, b — Radial stress for case B, c — Hoop stress for case B
Figure 6: Results for case C. a — Displacements for case C, b — Radial stress for case C, c — Hoop stress for case C
Figure 7: Errors of the plane-stress solution. a — Case A, b — Case B, c — Case C
Figure 8: Errors of the axi-symmetric solution. a — Case A, b — Case B, c — Case C
Figure 9: Errors of the full-3d solution. a — Case A, b — Case B, c — Case C
6 Parametric study
To be done.
7 Conclusions
According to figs. 4-6, the three finite-element solutions based on the displacement formulation of the elasticity equations seem to give reasonable solutions. But a closer look that takes the difference with respect to the continuous Lamé equations shows that the three cases behave in very different ways. Case A has a linear displacement field with a corresponding uniform stress distribution which can be reproduced by the FEM equations within the convergence tolerance of floating-point-based numerical methods. Case B shows a relatively good accuracy regarding displacements but a non-acceptable error on the stresses. Finally, Case C—which corresponds to the geometric parameters which might be found in piping-related engineering calculations—shows an acceptable accuracy in the evaluation of stresses within 1.5% with respect to the analytical solution.
The source of this large difference comes from the fact that the displacement field has a 1/r dependence on the radius, while the shape functions of the finite elements are usually quadratic in the spatial coordinate. Therefore, the smaller the radius, the less accurate the representation of 1/r with a parabola of r. Hence, for small values of r_i, care should be taken and a local mesh refinement needs to be performed in order to decrease the errors in the evaluation of stresses.
Now, even though displacement-based continuous finite elements can lead to potentially misleading results in some particular cases, piping-related computations can be effectively performed with this formulation without introducing uncertainties larger than the one that a mathematical model has, namely mechanical parameters, geometric imperfections, erection deviations, imperfect supports, etc. However, the exist other finite-elements formulations which can handle small radii without any further need of local mesh refinement—such as the equilibrium finite elements formulation—which might perform better in terms of efficiency and reduction of discretization errors.