Thick cantilever cylinder
← Previous: Fixed compressed cylinder | ↑ Index | Next: Cylinder embedded in another cylinder—smooth →
| Title | Thick cantilever cylinder |
| Tags | elasticity bending |
| Runnng time | a few minutes |
| See also | 075-fixed-compressed-cylinder |
| CAEplex case | https://caeplex.com/p/27235 |
| Available in | HTML PDF ePub |
1 Problem description
A cylinder or radius r=15~\text{mm} and length \ell = 70~\text{mm} along the x axis is clamped on the y-z plane fig. 1. A total force of F=1~\text{kN} in the negative y direction is uniformly distributed on the free face at x=\ell. The Young modulus is E=10~\text{GPa} and Poisson’s ratio is \nu = 0.35.
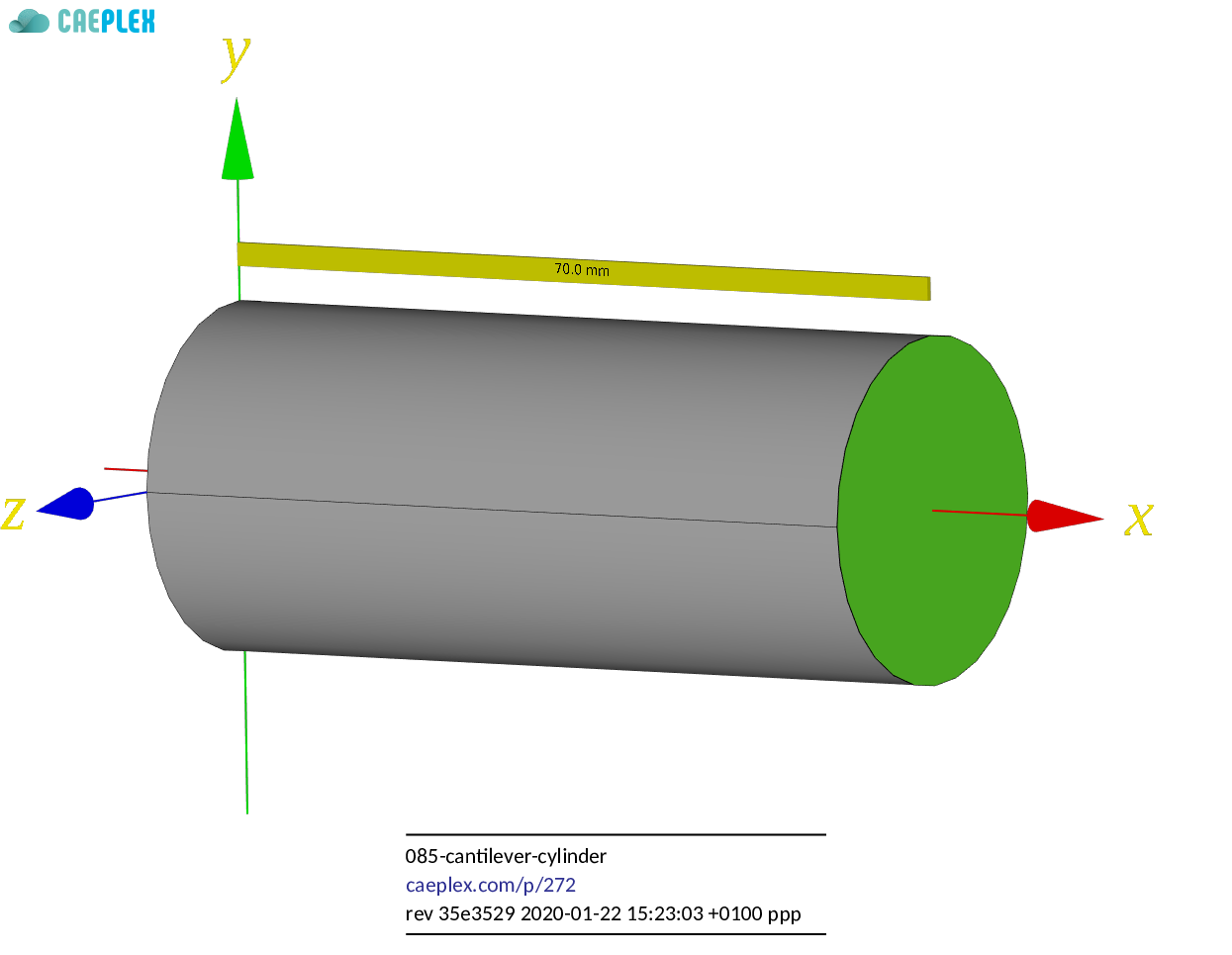
1.1 Expected results and further considerations
The vertical displacement evaluated at the center of the circular cross section (i.e. y=z=0) as a function of the axial coordinate x is expected to be computed by Fino—with different meshes—and compared to the Euler-Bernoulli and Timoshenko beam theories predictions. Once again, fully unstructured tetrahedral grids are to be used. The former theory predicts a vertical displacement
v_e(x) = \frac{F \cdot x^2 (3\ell - x)}{6 EI_z}
whilst the latter
v_t(x) = \frac{F \cdot x}{\kappa A G} - \frac{F (\ell-x)}{2 EI_z} \cdot \left[ \ell^2 - \frac{(\ell-x)^2}{3} \right] + \frac{F \ell^3}{3 EI_z}
where
- I_z=\pi/4 \cdot r^4 is the area’s moment of inertia with respect to the z axis,
- \kappa = 6(1+\nu)/(1+6\nu) is the Timoshenko shear coefficient for circular cross-sections,
- A=\pi \cdot r^2 is the cross-sectional area, and
- G = \frac{E}{2 (1+\nu)} is the material’s shear modulus.
In both cases, the maximum normal stress in the x direction is
\sigma_x = \frac{2 F \ell r}{I_z}
Note that these two theories are approximations which work better for long slender beams. In fact, the Euler-Bernoulli result does not depend on the Poisson’s ratio \nu—nor does the maximum normal stress.
2 Parametric study
First, a common set of keywords that define some physical values of problem is written in a separate file problem.fin which will be subsequently included in many main input files throughout this section:
# problem parameters
E = 10e3 # Young [ MPa ]
nu = 0.35 # Poisson
F = -1e3 # load in y direction [ N ]
# boundary conditions
PHYSICAL_GROUP NAME left BC fixed
PHYSICAL_GROUP NAME right BC Fy=FVery much like in Fixed compressed cylinder, a parametric run for a certain non-dimensional parameter c \in [20:90] is performed. Each run implies a different base characteristic element length \ell_c = 100~\text{mm}/c. The mesh template is
SetFactory("OpenCASCADE");
Merge "cantilever-cylinder.brep";
Physical Surface("left", 1) = {5};
Physical Surface("right", 2) = {6};
Physical Volume("bulk", 3) = {1};
Mesh.CharacteristicLengthMax = lc;
Mesh.Algorithm = 6;
Mesh.Algorithm3D = 1;
Mesh.ElementOrder = 2;
Mesh.Optimize = 1;
Mesh.OptimizeNetgen = 1;
Mesh.HighOrderOptimize = 2;Figs. 2 (a), 2 (b) show the two extreme grids used in the parametric run. The first one shows the full cylinder and the tetrahedra edges while the latter is a vertical cut where the faces of the volumetric elements can be seen.

Figure 2: Grid used for c=20 and c=90.. a — c=20, \ell_c=100/c=5~\text{mm}, 4k nodes, b — c=90, \ell_c=100/c=1.111\dots~\text{mm}, 210k nodes
# clamped cantilever cylinder subject to a bending load
r = 15 # radius [ mm ]
l = 70 # length [ mm ]
# parametric run over c
PARAMETRIC c MIN 20 MAX 90 STEP 10
lc = 100/c
# files
FILE geo fino-%d.geo c
FILE msh fino-%d.msh c
FILE vtk fino-%d.vtk c
OUTPUT_FILE full fino-full-%d.dat c
OUTPUT_FILE prof fino-profile-%d.dat c
# macro expansion, Gmsh invocation and msh reading
M4 INPUT_FILE_PATH cylinder-unstructured.geo.m4 OUTPUT_FILE geo EXPAND r EXPAND l EXPAND lc
# SHELL "if [ ! -e fino-%d.msh ]\; then gmsh -v 0 -3 fino-%d.geo\; fi" c c
MESH FILE msh
INCLUDE problem.fin
# numerical solution
FINO_STEP
# analytical solution
A = pi * r^2
I = pi/4 * r^4
G = 0.5*E/(1+nu)
kappa = 6*(1+nu)/(1+6*nu)
sigma_theory = -F*l*r/(0.5*I)
v_e(x) := F*x^2*(3*l-x)/(6*E*I)
v_t(x) := F*x/(kappa*A*G) - F*(l-x)/(2*E*I) * (l^2 - (l-x)^2/3) + F*l^3/(3*E*I)
v_f(x) := v(x, 0, 0)
# output of scalars as function of c
PRINT c %.4f lc %g nodes %.3f sigmax(0,r,0) -sigmax(0,-r,0) sigma_theory \
%.4f v(l,0,0) v_e(l) v_t(l) %.5f strain_energy
# output of distributions (one file for each c)
MESH_POST FILE vtk VECTOR u v w sigmax sigmay sigmaz tauxy tauyz tauzx
PRINT_FUNCTION FILE full u v w sigmax sigmay sigmaz tauxy tauyz tauzx
PRINT_FUNCTION FILE prof FORMAT %.10e v_f v_e v_t MIN 0 MAX l NSTEPS 100For each c, the ouput from Fino is
- the parameter c
- the characteristic element size \ell_c
- the number of nodes
- the maximum normal stress \sigma_x(0,r,0)
- minus the minimum normal stress -\sigma_x(0,-r,0) (which from theory should be numerically equal to \sigma_x(0,r,0))
- the maximum normal stress as predicted by the theory
- the vertical deflection at the center of the free face v(\ell,0,0)
- the vertical deflection predicted by Euler-Bernoulli
- the vertical deflection predicted by Timoshenko
- the strain energy U
3 Execution
$ fino parametric.fin
20 5.0000 3940 33.713 33.538 52.816 -0.3072 -0.2876 -0.2978 153.75221
30 3.3333 10701 35.247 37.467 52.816 -0.3075 -0.2876 -0.2978 153.92875
40 2.5000 22504 40.505 40.634 52.816 -0.3076 -0.2876 -0.2978 153.97976
50 2.0000 40222 44.273 40.733 52.816 -0.3077 -0.2876 -0.2978 154.00961
60 1.6667 68041 44.251 44.599 52.816 -0.3077 -0.2876 -0.2978 154.03700
70 1.4286 103017 48.086 47.158 52.816 -0.3078 -0.2876 -0.2978 154.05024
80 1.2500 149620 49.465 49.737 52.816 -0.3078 -0.2876 -0.2978 154.05755
90 1.1111 211814 51.604 50.657 52.816 -0.3078 -0.2876 -0.2978 154.06657
$4 Results
Figs. 3 (a), 3 (b), 4 (b) show the results of the parametric run.
Figure 3: Strain energy and normal stress vs. mesh size. a — Strain energy U vs. inverse of the number of nodes, b — Normal stresses \sigma_x at clamped end vs. inverse of the number of nodes
Figure 4: Vertical displacement profile and dependence with mesh size. a — Vertical displacement of the elastic line as a function of x for the two extreme meshes., b — Vertical displacement u at free end vs. inverse of the number of nodes
4.1 Discussion
The strain energy and the displacements seem to have converged yet the stresses do not even with 211k nodes. Even worse, the plotted stresses which should be strictly equal for every c are not. This fact further illustrates the difficulties of computing stresses out of displacements in cases like this one, even when there are nodes located explicitly at (0,\pm r, 0) to avoid interpolation errors. This difficulty will be further illustrated in the next section.
Fig. 4 (a) shows the vertical displacement v(x,0,0) at the center line along the x coordinate obtained with c=20 and with c=90, compared to both theoretical results. Euler-Bernoulli seems to give less deflections than Timoshenko, which in turn give less deflections than finite elements. It can be seen that the c=20 case is stiffer than c=90, which is a known and expected result: the coarser the mesh, the stiffer the discretized problem with respect to the continuous case. Hence, both theories underestimate the displacements so we can conclude that c=90 is closer to the actual solution than both theories.
5 Check
Before diving into the details of the computation of the same problem with other finite-element programs to further check the results obtained so far, it is illustrative to plot the relative differences between the vertical displacement of the elastic line computed with
- CalculiX,
- Sparselizard, and
- ANSYS
in the same plot.
In effect, fig. 5 shows the relative differences between all the cases discussed. Leaving aside the ANSYS results for now, which show interpolation issues, the difference with respect to CalculiX decreases as the mesh refinement increases—which is a good result. As for Sparselizard, the differences seem to be negligible. The following sections dive into the more difficult subject of stress computation.
5.1 CalculiX
The problem can be solved with CalculiX using this input with approx. 40k nodes and this one for 75k nodes. The following Fino input solves either problem (depending on the parameter passed in the command line which is the run-time expansion of the expression $1 in the file), reads back the FRD outputs (calculix-40k.frd or calculix-75k.frd), takes algebraic differences and writes them into a VTK file (fino-ccx-40k.vtk or fino-ccx-40k.vtk):
# clamped cantilever cylinder -- comparison to CalculiX
MESH NAME fino FILE_PATH fino-ccx-$1k.msh # read mesh for Fino (it is the same as in ccx)
INCLUDE problem.fin # include data to solve the problem
FINO_SOLVER ELEMENT_WEIGHT flat # mimic calculix' behaviour
FINO_STEP # solve the problem!
# read calculix output
MESH NAME ccx FILE_PATH calculix-$1k.frd DIMENSIONS 3 {
READ_FUNCTION D1
READ_FUNCTION D2
READ_FUNCTION D3
READ_FUNCTION SXX
READ_FUNCTION SYY
READ_FUNCTION SZZ
READ_FUNCTION SXY
READ_FUNCTION SYZ
READ_FUNCTION SZX
}
# compute differences
diff_u(x,y,z) := D1(x,y,z) - u(x,y,z)
diff_v(x,y,z) := D2(x,y,z) - v(x,y,z)
diff_w(x,y,z) := D3(x,y,z) - w(x,y,z)
diff_sigmax(x,y,z) := SXX(x,y,z) - sigmax(x,y,z)
diff_sigmay(x,y,z) := SYY(x,y,z) - sigmay(x,y,z)
diff_sigmaz(x,y,z) := SZZ(x,y,z) - sigmaz(x,y,z)
diff_tauxy(x,y,z) := SXY(x,y,z) - tauxy(x,y,z)
diff_tauyz(x,y,z) := SYZ(x,y,z) - tauyz(x,y,z)
diff_tauzx(x,y,z) := SZX(x,y,z) - tauzx(x,y,z)
# write differences in a vtk file
MESH_POST MESH fino FILE_PATH fino-ccx-$1k.vtk \
VECTOR diff_u diff_v diff_w \
diff_sigmax diff_sigmay diff_sigmaz \
diff_tauxy diff_tauyz diff_tauzx
# compute differences of displacements in the elastic line (picture above)
v_fino(x) := v(x, 0, 0)
v_ccx(x) := D2(x, 0, 0)
PRINT_FUNCTION FILE_PATH fino-ccx-$1k.dat FORMAT %.10e \
v_fino v_ccx v_fino(x)-v_ccx(x) \
(v_fino(x)-v_ccx(x))/v_fino(x) MIN 1 MAX 70 STEP 1
PRINT_FUNCTION FILE_PATH fino-full-$1k.dat FORMAT %.10e u v w sigmax sigmay sigmaz tauxy tauyz tauzx
PRINT_FUNCTION FILE_PATH ccx-full-$1k.dat FORMAT %.10e D1 D2 D3 SXX SYY SZZ SXY SYZ SZX
# report wall times
PRINT HEADER nodes time_wall_build time_wall_solve time_wall_stressThe geo file for the 40k case is
Merge "Pad_Geometry.brep";
Physical Surface("left", 1) = {5};
Physical Surface("right", 2) = {6};
Physical Volume("bulk",3 ) = {1};
Mesh.CharacteristicLengthMax = 2;
Mesh.Optimize = 1;
Mesh.OptimizeNetgen = 1;
Mesh.HighOrderOptimize = 1;
Mesh.ElementOrder = 2;
Mesh.Algorithm = 6;
Mesh.Algorithm3D = 1;
Mesh.MshFileVersion = 2.2;The requirement to use version 2.2 comes from two facts:
- it is easier to manually debug and check that the node coordinates are actually the same as in CalculiX’ input files, and
- we will be using the same mesh file for Sparselizard in sec. 5.2, which can only read version 2.2 meshes.
$ time ccx calculix-40k > /dev/null
real 0m33.572s
user 0m33.508s
sys 0m0.592s
$ time ccx calculix-75k > /dev/null
real 1m57.091s
user 1m56.846s
sys 0m0.792s
$
$ time fino fino-ccx.fin 40
# nodes time_wall_build time_wall_solve time_wall_stress
40366 1.14778 5.90176 0.387122
real 0m12.133s
user 0m15.290s
sys 0m8.800s
$ time fino fino-ccx.fin 75
# nodes time_wall_build time_wall_solve time_wall_stress
74748 2.37545 11.4841 0.716312
real 0m23.292s
user 0m26.894s
sys 0m10.618s
$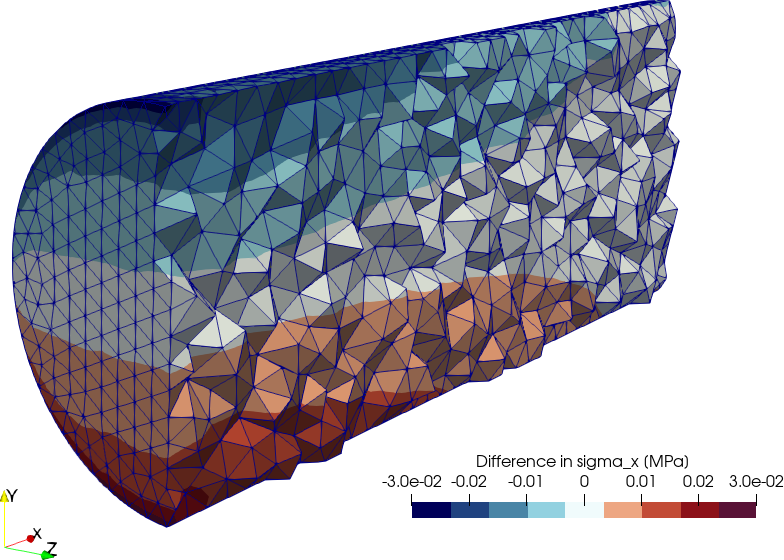
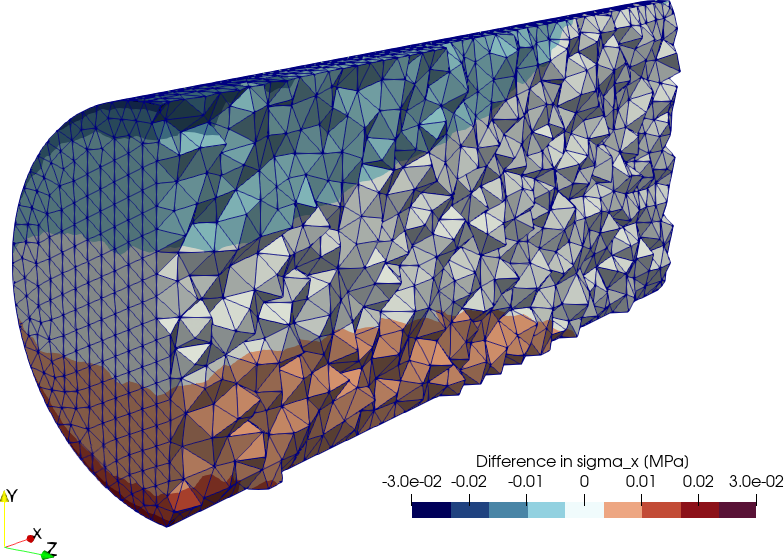
Figure 6: Absolute difference in \sigma_x between Fino and CalculiX. a — 40k nodes case, b — 75k nodes case
Figs. 6 (a), 6 (b) show the absolute difference of \sigma_x(x,y,z) in MPa as computed by Fino and CalculiX. The largest difference 0.03 MPa, which is negligible. It shoud be noted though, that if instead of using flat-element weighting by setting ELEMENT_WEIGHT to flat in Fino we left the default volume_times_quality the maximum difference would have been 3.5% in magnitude at some scattered locations. Fig. 7 illustrates dependence of \sigma_x at the external radius of clamped surface with the azimuthal angle \theta, with \theta=0 being the positive z direction. The individual bullets are actual nodes, so no interpolation is performed in the plot. It can be seen that
- the actual values computed by Fino and CalculiX coincide within a very narrow accuracy range, i.e. the black crosses are inside the salmon squares and the blue plus signs are inside the tan circles (the figures are vectors so they can be arbitrarily zoomed in), and
- finer meshes do not smooth out the spatial dependence.
5.2 Sparselizard
In order to solve the 40k & 75k problems with Sparselizard, this main source is used:
#include "sparselizardbase.h"
using namespace mathop;
void sparselizard(char *s) {
double x;
char msh_path[64];
char dat_path[64];
char vtk_path[64];
FILE *dat;
snprintf(dat_path, 63, "lizard-profile-%sk.dat", s);
snprintf(msh_path, 63, "fino-ccx-%sk.msh", s);
snprintf(vtk_path, 63, "lizard-sigmax-%sk.vtk", s);
int left = 1, right = 2, bulk = 3; // numerical values of physical groups in the mesh
mesh mymesh(msh_path);
double young = 10e3;
double poisson = 0.35;
double lambda = young * poisson/((1+poisson)*(1-2*poisson));
double mu = 0.5*young/(1+poisson);
wallclock clk;
formulation elasticity;
field u("h1xyz");
u.setorder(bulk, 2);
u.setconstraint(left);
parameter E, nu;
E|bulk = 10e3; nu|bulk = 0.35;
elasticity += integral(bulk, predefinedelasticity(dof(u), tf(u), E, nu));
elasticity += integral(right, array1x3(0,-1000/(M_PI*15*15),0)*tf(u));
solve(elasticity);
clk.print("Total calc time:");
dat = fopen(dat_path,"w"); // write profile at x,0,0
for (x = 0; x <= 70; x += 1) {
fprintf(dat, "%g\t%.10e\n", x, compy(u).interpolate(bulk, {x, 0, 0})[0]);
}
fclose(dat);
expression H(6,6,{lambda+2*mu, lambda, lambda, 0, 0, 0,
lambda, lambda+2*mu, lambda, 0, 0, 0,
lambda, lambda, lambda+2*mu, 0, 0, 0,
0, 0, 0, mu, 0, 0,
0, 0, 0, 0, mu, 0,
0, 0, 0, 0, 0, mu});
expression stress = H*strain(u);
comp(0, stress).write(bulk, vtk_path, 2);
}
int main(int argc, char **argv) {
SlepcInitialize(0,{},0,0);
sparselizard(argv[1]);
SlepcFinalize();
return 0;
}
$ time ./run_sparselizard.sh 40
Loading mesh from file 'fino-ccx-40k.msh'
Extracted 40366 nodes
Extracted 34641 lines with curvature order 2
Extracted 55402 triangles with curvature order 2
Extracted 26485 tetrahedra with curvature order 2
Time to load the mesh:
173.546 ms
Total calc time:
10.367 s
real 0m11.597s
user 1m6.450s
sys 0m2.362s
$ time ./run_sparselizard.sh 75
Loading mesh from file 'fino-ccx-75k.msh'
Extracted 74748 nodes
Extracted 64371 lines with curvature order 2
Extracted 104253 triangles with curvature order 2
Extracted 50258 tetrahedra with curvature order 2
Time to load the mesh:
325.969 ms
Total calc time:
26.9018 s
real 0m29.136s
user 2m46.125s
sys 0m8.048s
$ We already have seen that displacements computed by Sparselizard almost exactly coincide with Fino—something similar already occurred in Fixed compressed cylinder. Now, when we switch to analyze the stresses there is a catch: Sparselizard does not compute smoothed nodal values. In other words, instead of weighting and averaging the contributions from all the elements that share a node to obtain a single stress value for each node—as most other FEA programs do by default—it keeps the individual contributions of each element and creates as many nodes (with the same coordinates) as elements share the node in question—very much like the “never-average” option in Two cubes of different materials. Therefore, the VTK output shows discontinuities in the stresses at the element interfaces. In effect, figs. 8 (a), 8 (b) illustrate the difference of the two approaches which is so subtle that a detailed inspection of the figures is needed in order to spot the differences.
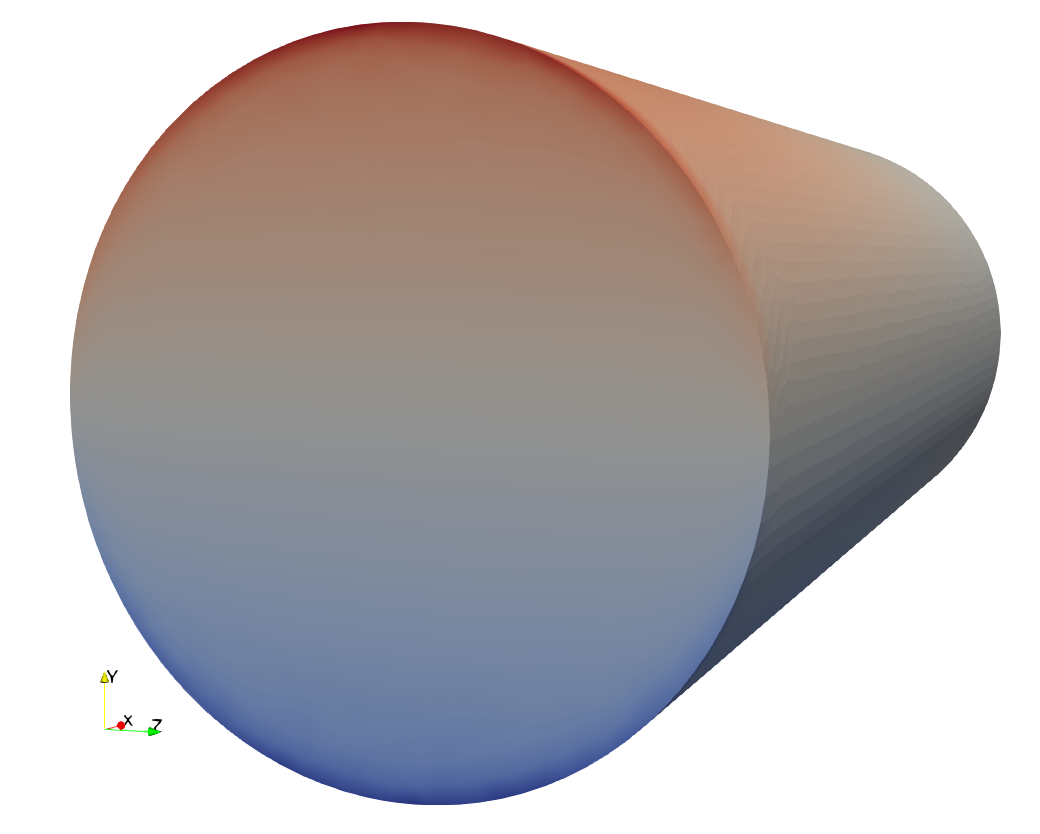

Figure 8: Stresses as computed by Fino (smoothed) and by Sparselizard (un-smoothed).. a — Smoothed stresses as computed by Fino., b — Un-smoothed stresses as computed by Sparselizard.
The latter behavior corresponds to setting Fino in “never-average” (a.k.a “rough”) mode (as opposed to the default “always” or “smooth” mode, see Two cubes of different materials). It can be triggered with the SMOOTH never keyword in the FINO_SOLVER definition. Indeed, let us solve the 40k & 75k problems with Fino in never-averaging mode to see what the azimuthal dependence of the normal stress \sigma_x is.
# clamped cantilever cylinder -- comparison to Sparselizard
FINO_SOLVER SMOOTH never # switch to “rough” mode, i.e. do not smooth stresses out
MESH NAME fino FILE_PATH fino-ccx-$1k.msh # same input mesh as in CalculiX
INCLUDE problem.fin
FINO_STEP
MESH_POST FILE_PATH rough-$1k.vtk sigmax
PRINT_FUNCTION FILE_PATH rough-full-$1k.dat 0 0 0 sigmax 0 0 0 0 0
MESH NAME lizard FILE_PATH lizard-sigmax-$1k.vtk DIMENSIONS 3 READ_SCALAR lizard AS SXX
PRINT_FUNCTION FILE_PATH lizard-full-$1k.dat 0 0 0 SXX 0 0 0 0 0
FUNCTION v_lizard(x) FILE_PATH lizard-profile-$1k.dat
FUNCTION v_fino(x) FILE_PATH fino-lizard-$1k.dat
PRINT_FUNCTION FILE_PATH fino-lizard-$1k.dat FORMAT %.10e \
v_fino v_lizard v_fino(x)-v_lizard(x) \
(v_fino(x)-v_lizard(x))/v_fino(x) MIN 1 MAX 70 STEP 1
PRINT HEADER nodes time_wall_build time_wall_solve time_wall_stress$ time fino fino-lizard.fin 40
# nodes time_wall_build time_wall_solve time_wall_stress
40366 1.31239 5.94183 0.587989
real 0m12.454s
user 0m14.542s
sys 0m9.798s
$ time fino fino-lizard.fin 75
# nodes time_wall_build time_wall_solve time_wall_stress
74748 2.52677 11.9084 1.1178
real 0m23.452s
user 0m25.596s
sys 0m12.108s
$ Even though figure fig. 8 (b) does not seem to be so much rougher than the smooth fig. 8 (a), numerical data in fig. 9 (a) showing the azimuthal dependence of the normal stress \sigma_x justifies the usage of the adjective “rough.” Now, each node of the original mesh does not have only one assigned stress value but as many as elements are sharing said node. This means that for the same angle \theta, there might be up to ten different values of stress. In “smooth” mode (i.e. the default for most standard finite-element programs) these contributions are averaged and the resulting value is assigned to the node.
The dispersion is larger for \pm 90º which are the angles where normal stresses are extrema. The detail of thirty degrees around \theta=-90º shown in fig. 9 (b) further confirms that the stresses computed by Sparselizard and by Fino (in rough mode) coincide—the black crosses and blue plus signs are inside the salmon squares and tan circles.
Figure 9: Azimuthal distribution of \sigma_x at the external radius of the clamped surface with Sparselizard.. a — Full range, b — Range [-105:-75] degrees
In view of these results, we can say that
- Fig. 7 does not seem as rough as it seemed the first time we saw it,
- Fig. 8 (b) is rougher than it seemed the first time we saw it, and
- Individual contributions to the averaged nodal values can have a wide distribution spread around the final averaged value. In the current case it can be up to 40%.
5.3 ANSYS
Nick Stevens, as in Fixed compressed cylinder, has kindly solved the cantilever problem with ANSYS. The displacements were already presented in fig. 5. It should be noted that even though the number of nodes is approximately the same, the mesh used by Nick for solving the problem with ANSYS (fig. 10 (a)) is not the same as any of the previous meshes used so far. Fig. 10 (b) shows the azimuthal distribution of the normal stress \sigma_x.
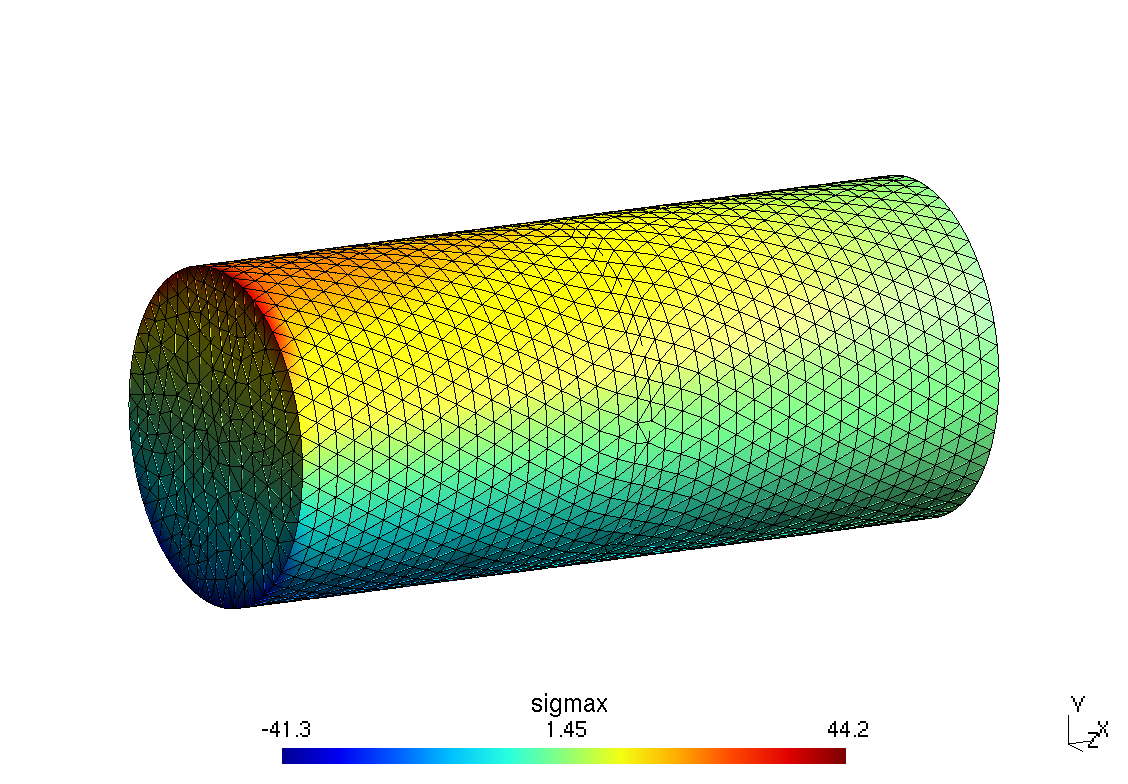
Figure 10: Results obtained using ANSYS. a — Normal stress computed with ANSYS., b — Azimuthal distribution of \sigma_x at the external radius of the clamped surface with ANSYS.
6 Extra check
The preceeding results seem to indicate that there is an essential difference between the finite element calculation and the analytical values developed by Euler, Bernoulli, Timoshenko and friends. Yet still there is another twist we can take. Let us consider now a an structured grid coming from extrusions (fig. 11 (a)):
SetFactory("OpenCASCADE");
Point(1) = {0,0,0};
Extrude {70, 0, 0} {
Point{1}; Layers{32}; Recombine;
}
Extrude {0, 15, 0} {
Curve{1}; Layers{12}; Recombine;
}
Extrude {{1, 0, 0}, {0, 0, 0}, Pi} {
Surface{1}; Layers{16}; Recombine;
}
Extrude {{1, 0, 0}, {0, 0, 0}, -Pi} {
Surface{1}; Layers{16}; Recombine;
}
Coherence;
Physical Surface("left") = {6, 2};
Physical Surface("right") = {7, 3};
Physical Volume("bulk") = {2, 1};
Mesh.ElementOrder = 2;
Mesh.SecondOrderIncomplete = 1;
Figure 11: Results using using a structured grid composed of hexahedra and wegdes.. a — Structured mesh created in Gmsh out of extrusions with \approx 50k nodes., b — Azimuthal distribution of \sigma_x at the external radius of the clamped surface computed with Fino using an structured grid.
MESH FILE_PATH cylinder-structured.msh
FINO_SOLVER PROGRESS_ASCII
INCLUDE problem.fin
FINO_STEP
MESH_POST FILE_PATH fino-structured.msh VECTOR u v w sigmax sigmay sigmaz tauxy tauyz tauzx
PRINT_FUNCTION FILE_PATH fino-structured.dat FORMAT %.10e u v w sigmax sigmay sigmaz tauxy tauyz tauzxFig. 11 (b) finally shows us that the agreement between the numerical and the analytical results is remarkable after all. The differences we found earlier are to be directly linked to the unstructured nature of the elements and the errors committed when computing the derivatives of the displacements using distorted elements (as thoroughly studied in case Stresses in a 10-node tetrahedron with prescribed displacements) rather than to the discrete nature of the displacement-based finite-element formulation.
Once again, it is noteworthy that even with a relatively large number of nodes, uncertainties in the order of 10% are to be expected when using unstructured grids even for simple geometries and smoothing of nodal values. Uncertainties of at least the same magnitude are therefore expected in more complex geometries where unstructured meshes are unavoidable.