Tensile test specimen
| Title | Tensile test specimen |
| Tags | elasticity reactions |
| Runnng time | 10 secs |
| CAEplex case | https://caeplex.com/p/41dd1 |
| Available in | HTML PDF ePub |
1 Foreword
This first case serves as a basic example to answer the first validation question: does Fino do what a FEA program is supposed to do? It also illustrates its design basis and the philosophy behind its implementation. A quotation from Eric Raymond’s The Art of Unix Programming helps to illustrate this idea:
Doug McIlroy, the inventor of Unix pipes and one of the founders of the Unix tradition, had this to say at the time:
Make each program do one thing well. To do a new job, build afresh rather than complicate old programs by adding new features.
Expect the output of every program to become the input to another, as yet unknown, program. Don’t clutter output with extraneous information. Avoid stringently columnar or binary input formats. Don’t insist on interactive input.
[…]
He later summarized it this way (quoted in “A Quarter Century of Unix” in 1994):
- This is the Unix philosophy: Write programs that do one thing and do it well. Write programs to work together. Write programs to handle text streams, because that is a universal interface.
Keep in mind that even though the quotes above and many FEA programs that are still mainstream today date both from the early 1970s, fifty years later they still
- Do not make just only one thing well.
- Do complicate old programs by adding new features.
- Do not expect the their output to become the input to another.
- Do clutter output with extraneous information.
- Do use stringently columnar and/or binary input (and output!) formats.
- Do insist on interactive output.
A further note is that not only is Fino both free and open-source software but it also is designed to connect and to work with (rule of composition) other free and open source software, like Gmsh, ParaView, Gnuplot, Pyxplot, Pandoc, TeX, and many others, including of course the operating system GNU/Linux. In particular, this report has been created from scratch using free and open source software only. Even the terminal recorder used to show the actual execution is GPLv3.
Fino also makes use of high-quality free and open source mathematical libraries which contain numerical methods designed by mathematicians and programmed by professional programmers, such as GNU Scientific Library, PETSc, SLEPc (optional) and all its respective dependencies. This way, Fino bounds its scope to do only one thing and to do it well: to build and solve finite-element formulations of thermo-mechanical problems. And it does so on high grounds, both
ethical: since it is free software, all users can
- run,
- share,
- modify, and/or
- re-share their modifications.
If a user cannot read or write code to make Fino suit her needs, at least she has the freedom to hire someone to do it for her, and
technological: since it is open source, advanced users can detect and correct bugs and even improve the algorithms. Given enough eyeballs, all bugs are shallow.
The reader is encouraged to consider and to evaluate the differences (both advantages and disadvantages) between the approach proposed in this work with traditional thermo-mechanical FEA software. The Git repository containing Fino’s source code can be found at https://github.com/seamplex/fino.
2 Problem description
A tensile test specimen of nominal cross-sectional area A = 20~\text{mm} \times 5~\text{mm} = 100~\text{mm}^2 is fully fixed on one end (magenta surface) and a tensile load of F_x = 10~\text{kN} is applied at the other end (green surface). The Young modulus is E=200~\text{GPa} and the Poisson’s ratio is \nu=0.3.
Figure 1: Tensile test specimen CAD from CAEplex https://caeplex.com/p/41dd1 (rotate and zoom it).
2.1 Expected results
The displacements and stresses distribution within the geometry are to be obtained. Elongation along the x axis and a mild contraction in y (and even milder in z) are expected. The normal tension at the center of the specimen is to be checked to the theoretical solution \sigma_x = F_x/A and the reaction at the fixed end should balance the external load \mathbf{F} at the opposite face. Stress concentrations are expected to occur at sharp corners of the coupon.
3 Geometry and mesh
Following the general rule of performing only one thing well, and the particular rules of composition and parsimony, the generation of the set of nodes and elements required to perform a thermo-mechanical computation using the finite element method is outside of Fino’s scope. The finite-element mesh is an input to Fino.
In the particular case of the tensile test problem, the geometry is given as a STEP file. It is meshed by Gmsh (or, following the rule of diversity, any other meshing tool which can write meshes in MSH format keeping information about physical groups). A suitable mesh (fig. 2) can be created using the following tensile-test.geo file:
Merge "tensile-test-specimen.step"; // read the step file
Mesh.CharacteristicLengthMax = 1.5; // set the max element size lc
Mesh.ElementOrder = 2; // ask for second-order elements
// define physical groups for BCs and materials
// the name in the LHS has to appear in the Fino input
// the number in the RHS is the numerical id of the entity in the CAD file
Physical Surface ("left") = {1}; // left face, to be fixed
Physical Surface ("right") = {7}; // right face, will hold the load
Physical Volume ("bulk") = {1}; // bulk material elementsOut of the six lines, the first three are used to read the CAD file, to set the characteristic element size \ell_c = 1.5~\text{mm} and to ask for second-order 10-noded tetrahedra (by default Gmsh creates first-order 4-node tetrahedra). The last three lines define one physical group each:
- geometrical surface #1 as physical surface “left,” which will be set as fixed in the Fino input file,
- geometrical surface #7 as physical surface “right,” which will hold the load defined in the Fino input file, and
- the volumetric bulk material elements in geometrical volume #1.
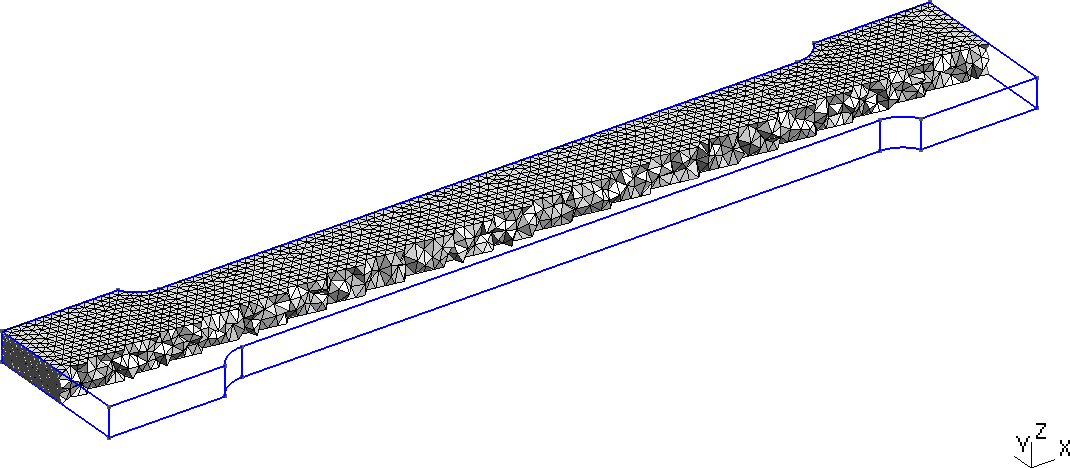
Figure 2: Tensile test specimen CAD, its geometrical entities and the resulting mesh.. a — Numerical ids of the surfaces in the original CAD., b — Three-dimensional mesh with uniform \ell_c=1.5~\text{mm} and \sim 50k nodes.
In general, multi-solid problems need to have different physical volumes in order to Fino to be able to set different mechanical properties. Even though this simple problem has a single solid, a physical volumetric group is needed in order to Gmsh to write the volumetric elements (i.e. tetrahedra) in the output MSH file.
The usage of physical groups to define boundary conditions follows the rule of representation as it folds knowledge into data instead of focusing on algorithmically setting loads on individual nodes. It also allows for extensibility since, for example, a mesh with many physical groups can be used for both a tensile and a bending cases where the first uses some groups and the latter other groups bringing clarity to the game.
4 Input file
Fino reads a plain-text input file—which in turns also reads the mesh generated above—that defines the problem, asks Fino to solve it and writes whatever output is needed. It is a syntactically-sweetened way to ask the computer to perform the actual computation (which is what computers do). This input file, as illustrated in the example below lives somewhere near the English language so a person can read through it from the top down to the bottom and more or less understand what is going on (rule of least surprise). Yet in the extreme case that the complexity of the problem asks for, the input file could be machine-generated by a script or a macro (rule of generation). Or if the circumstances call for an actual graphical interface for properly processing (both pre and post) the problem, the input file could be created by a separate cooperating front-end such as CAEplex in fig. 1 above (rule of separation). In any case, the input files—both for Gmsh and for Fino—can be tracked with Git in order to increase traceability and repeatability of engineering computations. This is not true for most of the other FEA tools avaialable today, particularly the ones that do not follow McIlroy’s recommendations above.
Given that the problem is relatively simple, following the rule of simplicity, the input file tensile-test.fin ought to be also simple. Other cases with more complexity such as parametric runs (such as Thick cantilever cylinder) or those that need to read results from other programs (such as Fixed compressed cylinder) in order to compare results might lead to more complex input files.
# tensile test example for Fino, see https://caeplex.com/p/41dd1
MESH FILE_PATH tensile-test.msh # mesh file in Gmsh format (either version 2.2 or 4.x)
# uniform properties given as scalar variables
E = 200e3 # [ MPa ] Young modulus = 200 GPa
nu = 0.3 # Poisson’s ratio
# boundary conditions ("left" and "right" come from the names in the mesh)
PHYSICAL_GROUP left BC fixed # fixed end
PHYSICAL_GROUP right BC Fx=1e4 # [ N ] load in x+
FINO_SOLVER PROGRESS_ASCII # print ascii progress bars (optional)
FINO_STEP # solve
# compute reaction force at fixed end
FINO_REACTION PHYSICAL_GROUP left RESULT R
# write results (Von Mises, principal and displacements) in a VTK file
MESH_POST FILE_PATH tensile-test.vtk sigma sigma1 sigma2 sigma3 VECTOR u v w
# print some results (otherwise output will be null)
PRINT "displ_max = " %.3f displ_max "mm"
PRINT "sigma_max = " %.1f sigma_max "MPa"
PRINT "principal1 at center = " %.8f sigma1(0,0,0) "MPa"
PRINT "reaction = [" %.3e R "] Newtons"
PRINT FILE_PATH tensile-sigma.dat %.0f sigma(0,0,0)- The mesh
tensile-test.mshis the output of Gmsh when invoked with the inputtensile-test.geoabove. It can be either version 4.1 or 2.2. - The mechanical properties, namely the Young modulus E and the Poisson’s ratio \nu are uniform in space. Therefore, they can be simply set using special variables
Eandnu. - Boundary conditions are set by referring to the physical surfaces defined in the mesh. The keyword
fixedis a shortcut for setting the individual displacements in each directionu=0,v=0andw=0. - An explicit location within the logical flow of the input file hast to be given where Fino ought to actually solve the problem with the keyword
FINO_STEP. It should be after defining the material properties and the boundary conditions and before computing secondary results (such as the reactions) and asking for outputs. - The reaction in the physical group “left” is computed after the problem is solved (i.e. after
FINO_STEP) and the result is stored in a vector namedRof size three. There is nothing special about the nameR, it could have been any other valid identifier name. - A post-processing output file in format VTK is created, containing:
- The von Mises stress
sigma(\sigma) as an scalar field - The three principal stresses
sigma1,sigma_2andsigma_3(\sigma_1, \sigma_2 and \sigma_3 respectively) as three scalar fields - The displacement vector \mathbf{u}=[u,v,w] as a three-dimensional vector field
- The von Mises stress
- Some results are printed to the terminal (i.e. the standard output) to summarize the run. Note that
- The actual output (including post-processing files) is 100% defined by the user, and
- If no output instructions are given in the input file (
PRINT,MESH_POST, etc.) then no output will be obtained.
- Finally, the von Mises stress \sigma(0,0,0) evaluated at the origin is written to an ASCII file
tensile-sigma.datrounded to the nearest integer (in MPa). This is used to test the outcome of Fino’s self-tests using themake checktarget in an automated way. Note that there is no need to have an actual node at \mathbf{x}=(0,0,0) since Fino (actually wasora) can evaluate functions at any arbitrary point.
5 Execution
Opening a terminal and calling both Gmsh and Fino in sequence should go as smooth (and as fast) as this:
Here is a static mimic of a 22-second terminal session:
$ gmsh -3 tensile-test.geo
Info : Running 'gmsh -3 tensile-test.geo' [Gmsh 4.5.2-git-2373007b0, 1 node, max. 1 thread]
Info : Started on Wed Jan 29 11:07:04 2020
Info : Reading 'tensile-test.geo'...
Info : Reading 'tensile-test-specimen.step'...
Info : - Label 'Shapes/ASSEMBLY/=>[0:1:1:2]/Pad' (3D)
Info : - Color (0.8, 0.8, 0.8) (3D & Surfaces)
Info : Done reading 'tensile-test-specimen.step'
Info : Done reading 'tensile-test.geo'
Info : Meshing 1D...
Info : [ 0 %] Meshing curve 1 (Line)
Info : [ 10 %] Meshing curve 2 (Line)
Info : [ 10 %] Meshing curve 3 (Line)
[...]
Info : [100 %] Meshing surface 14 order 2
Info : [100 %] Meshing volume 1 order 2
Info : Surface mesh: worst distortion = 0.90913 (0 elements in ]0, 0.2]); worst gamma = 0.722061
Info : Volume mesh: worst distortion = 0.824145 (0 elements in ]0, 0.2])
Info : Done meshing order 2 (1.32521 s)
Info : 49534 nodes 40321 elements
Info : Writing 'tensile-test.msh'...
Info : Done writing 'tensile-test.msh'
Info : Stopped on Wed Jan 29 11:07:07 2020
$ fino tensile-test.fin
....................................................................................................
----------------------------------------------------------------------------------------------------
====================================================================================================
displ_max = 0.076 mm
sigma_max = 160.2 MPa
principal1 at center = 99.99998119 MPa
reaction = [ -1.000e+04 -1.693e-04 -1.114e-03 ] Newtons
$- The three lines with the dots, dashes and double dashes are ASCII progress bars for the assembly of the stiffness matrix, the solution of the linear system and the computation of stresses, respectively. They are turned on with
PROGRESS_ASCII. - Almost any location within the input file where a numerical value is expected can be replaced by an algebraic expression, including standard functions like
log,exp,sin, etc. See wasora’s reference for details. - Once again, if the
MESH_POSTandPRINTinstructions were not included, there would not be any default output of the execution (rule of silence). This should be emphasized over and over, as I have recently (i.e. thirteen years after the commercial introduction of smartphones) stumbled upon a the output file of a classical FEM program that seems to have been executed in 1970: paginated ASCII text ready to be fed to a matrix-doy printed containing all the possible numerical output because the CPU cost of re-running the case of course overwhelms the hourly rate of the engineer that hast to understand the results. For more than fifty years (and counting), McIlroy’s second bullet from sec. 1 above has been blatantly ignored. - It has already been said that the output is 100% controlled by the user. Yet this fact includes not just what is written but also how: the precision of the printed results is controlled with
printfformat specifiers. Note the eight decimal positions in the evaluation of \sigma_1 at the origin, whilst the expected value was 100~\text{MPa} (the load is F_x=10^4~\text{N} and the cross-sectional area is 100~\text{mm}^2). - If available, the MUMPS Solver direct solver can be used instead of the default GAMG-preconditioned GMRES itearative solver by passing the option
--mumpsin the command line. More on solvers in sec. 8.2.
6 Results
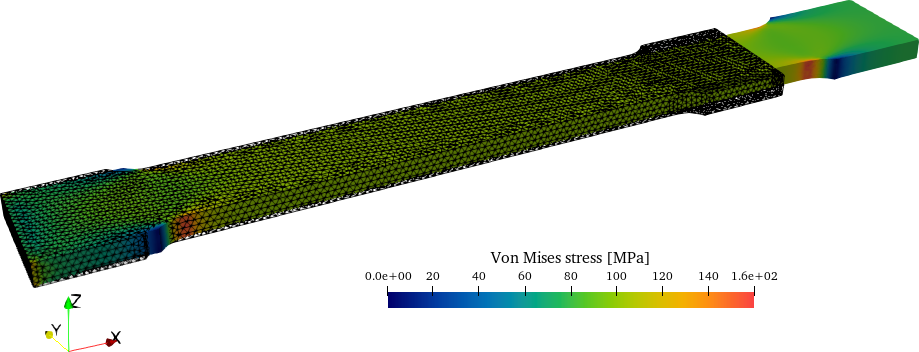
After the problem is solved and an appropriately-formatted output file is created, Fino’s job is considered done. In this case, the post-processing file is written using MESH_POST. The VTK output can be post-processed with the free and open source tool ParaView (or any other tool that reads VTK files such as Gmsh in post-processing mode), as illustrated in fig. 3.
6.1 Check
Qualitatively speaking, Fino does what a mechanical finite-element program is expected to do:
The displacement vector and scalar von Mises stress fields are computed by Fino, as they are successfully read by Paraview.
Elongation in the x direction and mild contractions in y and z are observed.
The principal stress \sigma_1 should be equal to F_x/A, where
- F_x=10^4~\text{N}, and
- A = 20~\text{mm} \times 5~\text{mm} = 100~\text{mm}^2.
In effect, \sigma_1(0,0,0) = 100~\text{MPa}.
The numerical reaction \mathbf{R} at the fixed end reported by Fino is
\mathbf{R} = \left[ \begin{matrix}-10^4 \\ \approx 10^{-4} \\ \approx 10^{-3}\end{matrix}\right] ~\text{N}
which serves as a consistency check.
Stress concentrations are obtained where they are expected.
7 Comparison
Just for the sake of validating that Fino does what a FEA program is supposed to do, let’s qualitatively compare how other programs solve the simple tensile test problem.
7.1 FreeCAD with CalculiX
FreeCAD is a free and open source parametric modeler based on the OpenCASCADE geometry kernel. FreeCAD can be used both as a GUI application and as a Python API, and the architecture allows for arbitrary plugins. One of these extensions is the possibility of interfacing with FEM programs, and the most mature of these interfaces is the one for the free and open source FEA tool CalculiX which is heavily based (and influenced) by the traditional FEA workflow. This might be a little bit cumbersome for newcomers unaware of workflows based on using programs designed fifty years ago.
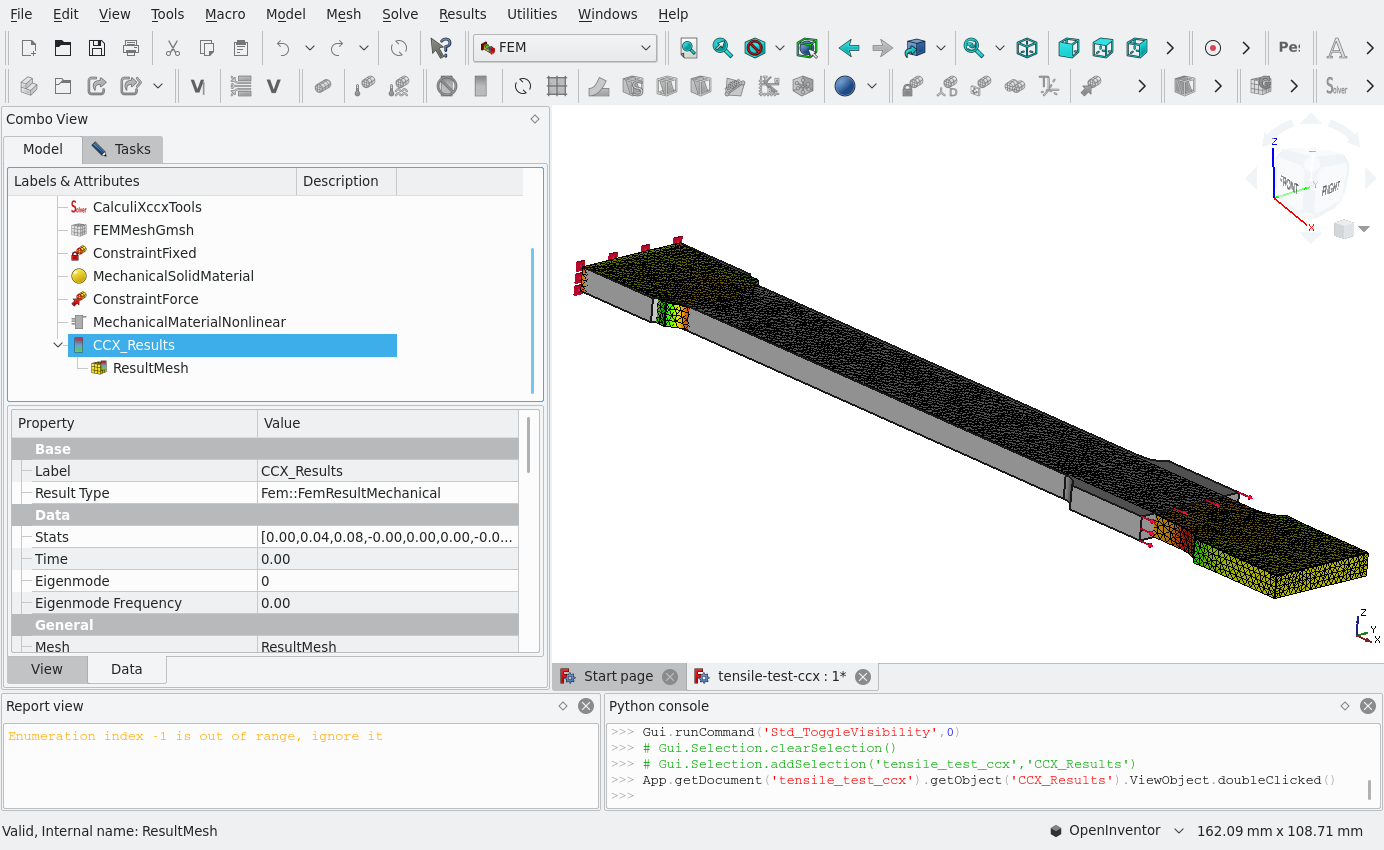
In any case, a FreeCAD file contains the geometry and all the definitions that CalculiX needs to solve the tensile test specimen subject fixed on one end and subject to a tensile load on the other. Fig. 4 shows the displacements warped 500 times (as in fig. 3) where the elongation in x, contraction in y and z and stress concentrations coincide with Fino’s and with what it is expected in this problem.
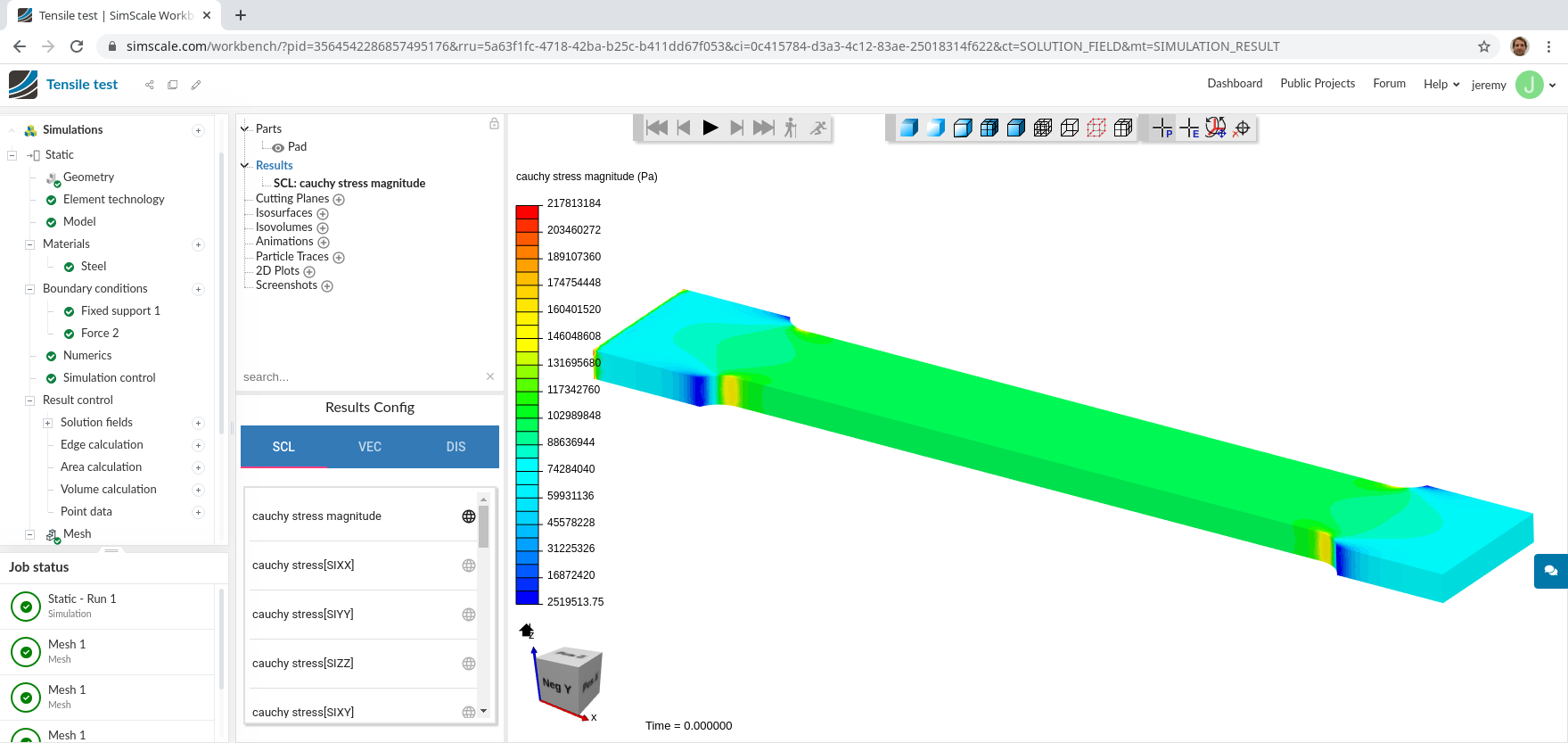
7.2 Simscale with CodeAster
Simscale is a German pioneering web platform for performing numerical analysis (i.e. “simulation”) in the cloud from the browser.1 It is a front-end for a number of third-party open source solvers, including the French Code_Aster for mechanical problems and OPENFOAM® for computational fluid dynamics.
8 Extra checks
The simple tensile test problem is qualitatively solved with Fino as expected. This section extends the validation to further check that Fino is solving the right equations.
8.1 Strain energy convergence
It is a well-known result from the mathematical theory that the displacement-based finite-element formulation gives a stiffer solution than the continuous problem. This means that the total strain energy U in load-driven (displacement-driven) problems is always lower (higher) than the exact physical value.
The following input files asks Fino to perform a parametric run on c \in [1:10] which controls the characteristic element size \ell_c=10~\text{mm}/c:
PARAMETRIC c MIN 1 MAX 10 STEP 1
lc = 10/c
M4 INPUT_FILE_PATH parametric.geo.m4 OUTPUT_FILE_PATH parametric.geo EXPAND lc
SHELL "gmsh -3 -v 0 parametric.geo"
MESH FILE_PATH parametric.msh
E = 200e3
nu = 0.3
PHYSICAL_GROUP left BC fixed
INCLUDE $1.fin # include either load or displ boundary condition
FINO_STEP
FINO_REACTION PHYSICAL_GROUP left RESULT R
PRINT c lc nodes %.4f strain_energy %.8f u(80,0,0) R(1) %.8f sigma1(0,0,0) %.3f time_wall_total %e memoryDepending on the command-line argument $1, it includes either load.fin
or displ.fin
$ fino parametric-energy.fin displ | tee displ.dat
10 10 1381 378.0254 0.07551236 -10012.19688820 100.12193130 0.393 5.705728e+07
20 5 3406 377.7806 0.07551234 -10005.87225589 100.05786431 1.416 1.020641e+08
30 3.33333 5934 377.7151 0.07551235 -10004.04718626 100.04035986 2.121 1.901896e+08
40 2.5 13173 377.6670 0.07551234 -10002.80454512 100.02703566 5.841 4.936827e+08
50 2 21897 377.6416 0.07551235 -10002.10898755 100.02189744 9.199 9.886843e+08
60 1.66667 36413 377.6316 0.07551234 -10001.84996627 100.01824358 20.676 1.319252e+09
70 1.42857 52883 377.6141 0.07551235 -10001.38248904 100.01358953 24.926 2.285650e+09
80 1.25 71568 377.6106 0.07551236 -10001.29858951 100.01271875 38.768 2.688750e+09
90 1.11111 103742 377.6026 0.07551235 -10001.09116871 100.01066954 67.782 3.595817e+09
100 1 136906 377.5994 0.07551234 -10000.99998694 100.00974332 90.248 4.684169e+09
$ fino parametric-energy.fin load | tee load.dat
10 10 1381 377.0997 0.07538952 -10000.00057800 99.99985582 0.826 5.935514e+07
20 5 3406 377.3440 0.07542967 -9999.99727028 99.99965822 2.036 1.042063e+08
30 3.33333 5934 377.4100 0.07544179 -10000.00700660 99.99980990 2.541 1.924178e+08
40 2.5 13173 377.4580 0.07545095 -9999.95509637 99.99981492 6.251 4.988027e+08
50 2 21897 377.4829 0.07545594 -9999.99976796 99.99974599 7.323 9.938166e+08
60 1.66667 36413 377.4938 0.07545809 -9999.97099411 99.99987546 14.838 1.328071e+09
70 1.42857 52883 377.5105 0.07546140 -9999.95702214 100.00028774 25.190 2.294686e+09
80 1.25 71568 377.5145 0.07546216 -9999.97300192 99.99997997 33.983 2.697781e+09
90 1.11111 103742 377.5201 0.07546350 -10000.04369761 99.99955431 45.707 3.604849e+09
100 1 136906 377.5267 0.07546443 -9999.93061385 100.00001476 99.697 4.685390e+09
$Indeed, fig. 6 shows that the total strain energy U is a monotonically increasing function of the number of nodes. Conversely, for the load-driven case it is monotonically decreasing, which is the expected behavior of a displacement-based finite-element program.
8.2 Performance
Let’s switch our attention briefly to the subject of performance, which is indeed related to what it is expected from a finite-element program. In the general case, the time needed to solve a finite-element problem depends on
- the size of the problem being solved,
- the number of the nodes in the mesh
- the number of degrees of freedom per node of the problem
- the particular problem being solved,
- the condition number of the stiffness matrix
- the non-zero structure of the stiffness matrix
- the computer used to solve the problem,
- the architecture, frequency and number of the CPU(s)
- the size, speed and number of memory cache levels
- implementation details of the operating-system scheduler
- the optimization flags used to compile the code
- the algorithms used to solve the system of equations
- preconditioner
- linear solver
- parallelization (or lack of)
As it has been already explained, Fino uses PETSc—pronounced PET-see (the S is silent). It is a suite of data structures and routines for the scalable (parallel) solution of scientific applications modeled by partial differential equations. In other words, it is a library programmed by professional programmers implementing state-of-the-art numerical methods developed by professional mathematicians. And yet, it is free and open source software.
PETSc provides a variety of linear solvers and preconditioners which can be used to solve the finite-element formulation. The choice of the type of preconditioner and linear solver can be done from the input file or directly from the command line. By default, mechanical problems are solved with the Geometric algebraic multigrid-preconditioned Generalized Minimal Residual method, which is an iterative solver. An alternative might be a direct sparse solver, such as the MUMPS Solver, which Fino (through PETSc’s interface) can use.
To get some insight about how the problem size, the computer and the algorithms impact in the time needed to solve the problem we perform another parametric run on c \in [1:12] in two different computers with three different solvers and pre-conditioners:
- Geometric Algebraic Multigrid preconditioner with Generalized Minimal Residual solver (default)
- LU direct solver used as a preconditoner
- Cholesky-preconditioned direct MUMPS solver
FINO_SOLVER PC_TYPE $1 # either gamg, lu or mumps (read from commandline)
PARAMETRIC c MIN 1 MAX 12 STEP 1
lc = 10/c
FILE msh parametric-%d.msh c
MESH FILE msh
E = 200e3
nu = 0.3
PHYSICAL_GROUP left BC fixed
PHYSICAL_GROUP right BC Fx=1e4
FINO_STEP
PRINT c lc nodes %e time_wall_total memory time_wall_build time_wall_solve time_wall_stress $ for i in gamg lu mumps; do fino parametric-solver.fin $i > `hostname`-${i}.dat; done
$Figure 7: Wall time needed to solve the linear problem as a function of the number of nodes in two different computers. a — High-end desktop computer, b — Virtual server running on the cloud
Fig. 7 shows the dependence of the wall time needed to solve the linear problem with respect to the number of nodes in two different computers. Only the time needed to solve the linear problem is plotted. That is to say, the time needed to mesh the geometry, to build the matrix and to compute the stresses out of the displacements is not taken into account. The reported times correspond to only one process, i.e. Fino is run in serial mode with no parallelization requested. It can be seen that direct solvers are faster than the iterative method for small problems. Yet GAMG scales better and for a certain problem size (which depends on the hardware and more importantly on the particular problem being solved) its performance is better than that of the direct solvers. This is a known result, which can be stated as direct solvers are robust but not scalable.2
Fino defaults to GAMG+GMRES since this combination is provided natively by PETSc and does not need any extra library (as in the MUMPS case), but it still sticks to the rule of optimization. Chances are that another combination of preconditioner, solver (and hardware!) might be better suitable for the problem being solved. It is up to the user to measure and to choose the most convenient configuration to obtain results as efficiently as possible.
As a final comment, although Fino provides basic parallelization capabilities there is still room to optimize the code regarding distributed computing. Fig. 8 shows the wall time needed to solve the c=10 case in the VPS with up to eight CPUs. The time does decrease but not as the inverse of the number of processes.
Not that Simscale was the inspiration for CAEplex but when I discovered its existence in 2015 it confirmed that my idea that doing something like CAEplex was viable.↩︎
See second bullet of slide #6 in http://www.mcs.anl.gov/petsc/petsc-20/tutorial/PETSc3.pdf.↩︎