Cube under pure tension
| Title | Cube under pure tension |
| Tags | elasticity tension |
| Runnng time | 1 sec |
| See also | 006-cylinder-pure-compression |
| CAEplex case | https://caeplex.com/p/26d55 |
| Available in | HTML PDF ePub |
1 Problem description
A non-dimensional cube of size 1 \times 1 \times 1 with one corner at the origin and faces parallel to the coordinate planes is subject to a total non-dimensional tensile force of 1 unit in the positive x direction acting on the face at x=1 (fig. 1). The cube has a non-dimensional unitary Young modulus E=1 and Poisson’s ratio \nu=0.3 The face on the x-y plane is forced to have a null displacement in the x direction (u=0) but it is free to deform in any of the other two directions. To remove the rigid body displacements, the point located at the origin is fixed in its three degrees of freedom and the edge in the z axis is restrained to move in the y direction (v=0). See Cylinder under pure compression for an alternate way of removing the rigid body displacements while keeping pure tension stresses.
The displacements and stresses distribution within the cube are to be obtained. The stress \sigma_x is expected to be uniformly equal to one with the other five stress components (\sigma_y, \sigma_z, \tau_{xy}, \tau_{yz} and \tau_{zx}) to be identically equal to zero. The cube is expected to expand in the x direction and to contract in both the y and z directions due to the non-zero Poisson’s ratio \nu.
The mesh is expected to be fully unstructured and not optimized as to show that the expected results are recovered with the numerical calculation independently of having a mesh composed of regular hexahedra with faces parallel to the full geometry. Even in the case of an unstructured tetrahedral grid, the total surface of the loaded face will still add up to the actual surface of the continuous cube even when using large elements. Hence, a total force can be used as a boundary condition. If the face was curved then the actual discretized area would depend on the the grid size and the same total force would be distributed differently on the actual nodes for different discretized areas, which is the case in Cylinder under pure compression.
2 Geometry and mesh
The geometry is created and meshed directly from Gmsh. Physical groups which will hold boundary conditions are defined in the cube.geo file. The mesh is unstructured tetrahedral due to the reasons already explained.
SetFactory("OpenCASCADE");
Box(1) = {0, 0, 0, 1, 1, 1}; // the cube itself
// physical groups for boundary conditions
Physical Point("origin") = {2};
Physical Curve("zee") = {1};
Physical Curve("wye") = {4};
Physical Surface("left") = {1};
Physical Surface("right") = {2};
// this one is needed to get volumetric elements in the .msh
Physical Volume("bulk") = {1};
// meshing options
Mesh.CharacteristicLengthMax = 0.15;
Mesh.ElementOrder = 2;3 Input file
The annotated input file cube.fin is self-explanatory. It solves the problem and writes a VTK file. To obain a pure tension condition, the fixed face is not fully fixed but only restricted to move in the normal direction. In addition, the rigid-body displacements are removed by fixing an edge and a vertex.
MESH FILE_PATH cube.msh # read mesh
E = 1 # unitary Young modulus
nu = 0.3 # non-zero Poisson's ratio
# displacement boundary conditions
PHYSICAL_GROUP origin BC fixed
PHYSICAL_GROUP zee BC v=0
PHYSICAL_GROUP left BC u=0
# load boundary condition
PHYSICAL_GROUP right BC Fx=1
FINO_STEP # solve problem
# write post-processing VTK file
MESH_POST FILE_PATH cube.vtk VECTOR u v w sigmax sigmay sigmaz tauxy tauyz tauzx
4 Execution
$ gmsh -v 0 -3 cube.geo
$ fino cube.fin
$Recall Fino follows the UNIX rule of silence. And Gmsh can be silenced by setting its verbosity to zero with -v 0.
5 Results
The VTK output can be post-processed with the free tool ParaView as shown in fig. 2.
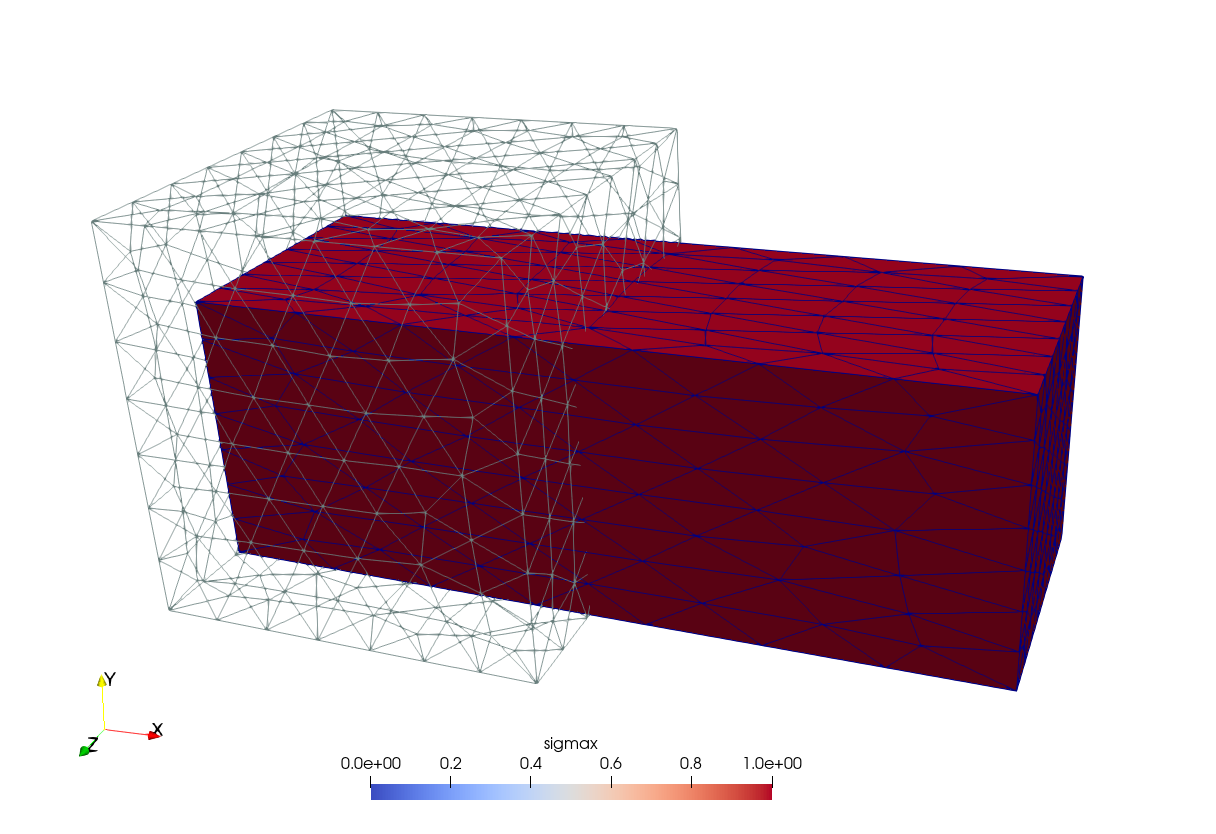

Figure 2: Stresses over the displaced grid and comparison with the original cube.. a — \sigma_x, b — \sigma_y
5.1 Check
The \sigma_x(x,y,z) distribution is expected to be identically equal to one and all the other five stresses \sigma_y, \sigma_z, \tau_{xy}, \tau_{yz} and \tau_{zx} are expected to vanish. To verify this is the case, the following input file is built which includes the basic solution, finds the maximum and minimum values of all the six stresses and prints them out in the standard output.
It should be noted that for this particular case, the stresses do not depend on the mesh coarsenes. Instead, they depend only on the precision of the linear solver used to compute the displacements. In the following check, the variable fino_reltol—which controls the relative tolerance of the default iterative linear solver residual for the displacements and defaults to 10^{-6}—is read form the commandline so as to verify that the results do depend on the convergence of the solver.
fino_reltol = $1
INCLUDE cube.fin
# compute min/max stresses
MESH_FIND_MINMAX FUNCTION sigmax MIN sigmax_min MAX sigmax_max
MESH_FIND_MINMAX FUNCTION sigmay MIN sigmay_min MAX sigmay_max
MESH_FIND_MINMAX FUNCTION sigmaz MIN sigmaz_min MAX sigmaz_max
MESH_FIND_MINMAX FUNCTION tauxy MIN tauxy_min MAX tauxy_max
MESH_FIND_MINMAX FUNCTION tauyz MIN tauyz_min MAX tauyz_max
MESH_FIND_MINMAX FUNCTION tauzx MIN tauzx_min MAX tauzx_max
PRINT "stress\tmin\t\tmax"
PRINT SEP "\t" "% +5e" "sigmax" sigmax_min sigmax_max
PRINT SEP "\t" "% .5e" "sigmay" sigmay_min sigmay_max
PRINT SEP "\t" "% .5e" "sigmaz" sigmaz_min sigmaz_max
PRINT SEP "\t" "% .5e" "tauxy" tauxy_min tauxy_max
PRINT SEP "\t" "% .5e" "tauyz" tauyz_min tauyz_max
PRINT SEP "\t" "% .5e" "tauzx" tauzx_min tauzx_max
$ fino check.fin 1e-3
stress min max
sigmax +9.957418e-01 +1.006068e+00
sigmay -3.13405e-03 7.79247e-03
sigmaz -3.52270e-03 3.82543e-03
tauxy -2.15554e-03 4.23122e-03
tauyz -1.19436e-03 1.43105e-03
tauzx -1.33109e-03 1.85007e-03
$ fino check.fin 1e-6
stress min max
sigmax +9.999914e-01 +1.000004e+00
sigmay -7.12178e-06 4.23256e-06
sigmaz -5.30028e-06 3.86275e-06
tauxy -3.51029e-06 2.84792e-06
tauyz -1.81021e-06 2.14615e-06
tauzx -3.16928e-06 2.78318e-06
$ fino check.fin 1e-9
stress min max
sigmax +1.000000e+00 +1.000000e+00
sigmay -3.78926e-09 3.49065e-09
sigmaz -4.78977e-09 4.75662e-09
tauxy -1.38614e-09 1.98276e-09
tauyz -1.74491e-09 1.49083e-09
tauzx -1.64074e-09 2.51987e-09
$ Note that if instead of the default GAMG-preconditioned GMRES iterative solver, we could have asked Fino to use a direct solver like MUMPS Solver—passing --mumps as an option for instance. In this case, the outputs would have been always the same as the tolerance fino_reltol only applies to iterative solvers and does not affect direct ones.