NAFEMS LE1 plane-stress benchmark
← Previous: Cylinder under pure compression | ↑ Index | Next: NAFEMS LE10 thick plate pressure benchmark →
| Title | NAFEMS LE1 plane-stress benchmark |
| Tags | NAFEMS benchmark plane stress |
| Runnng time | 10 secs |
| See also | 012-nafems-le10 |
| Available in | HTML PDF ePub |
1 Problem description
This problem is known as the NAFEMS LE1 plane-stress benchmark and has been introduced in 1986 as the first problem of The Standard NAFEMS Benchmarks. There are public solutions available online using a wide variety of FEA solvers such as this, this, this, this and this one. Do not hesitate contacting us if you want to add another reference to the list.
As shown in fig. 1, the problem consists of a plane-stress membrane defined by two ellipses. The membrane subject to a tension traction condition p=10~\text{MPa} on its outermost edge. Due to symmetry, only one quarter of the membrane needs to be modeled. Material’s Young modulus is E=210~\text{GPa} and Poisson’s ratio is \nu=0.3. The objective is to compute the normal stress in the y direction at the lower inside corner D=(2~\text{m},0).
1.1 Expected results
The reference solution given in the original NAFEMS book is \sigma_y = 92.7~\text{MPa}.
2 Geometry and mesh
Both the geometry and the mesh are created in Gmsh using the OpenCASCADE kernel with the following input file:
// NAFEMS LE1 plane-stress benchmark geometry & mesh
SetFactory("OpenCASCADE");
// create the geometry
a = 1000;
b = 2750;
c = 3250;
d = 2000;
// define the four points
Point(1) = {0, a, 0};
Point(2) = {0, b, 0};
Point(3) = {c, 0, 0};
Point(4) = {d, 0, 0};
// join them with the ellipses and straight edges
Line(1) = {1, 2};
Ellipse (2) = {0,0,0, c, b, 0, Pi/2};
Line(3) = {3, 4};
Ellipse (4) = {0,0,0, d, a, 0, Pi/2};
// merge the points
Coherence;
// create the surface
Curve Loop(1) = {1, -2, 3, 4};
Plane Surface(1) = {1};
// define physical groups
Physical Point("A",1) = {1};
Physical Point("B",2) = {2};
Physical Point("C",3) = {3};
Physical Point("D",4) = {4};
Physical Curve("AB",5) = {1};
Physical Curve("BC",6) = {2};
Physical Curve("CD",7) = {3};
Physical Curve("DA",8) = {4};
Physical Surface("bulk",9 ) = {1};
// ask for second-order curved complete elements (i.e. quad9)
Mesh.ElementOrder = 2;
Mesh.RecombineAll = 1;
Mesh.SecondOrderIncomplete = 0;
Mesh.SecondOrderLinear = 0;
Mesh.CharacteristicLengthMax = 40;
// use transfinite algoritmh to obtain a structured grid
Transfinite Curve{1,3} = 2000/(Mesh.CharacteristicLengthMax * Mesh.CharacteristicLengthFactor);
Transfinite Curve{2,4} = 3000/(Mesh.CharacteristicLengthMax * Mesh.CharacteristicLengthFactor);
Transfinite Surface{1};In this base case, second-order curved nine-node quadrangles are used to mesh the geometry (see The NAFEMS Benchmark Challenge #1 for a discussion about different quadrangular elements). Using the transfinite algorithm, a structured grid with 14,751 nodes and 3,876 elements is obtained (fig. 2).
3 Input file
The input file which asks Fino to solve the problem is fairly simple:
MESH FILE_PATH le1-base.msh DIMENSIONS 2 # read mesh
FINO_PROBLEM PLANE_STRESS # set problem type
# material properties
E = 210e3
nu = 0.3
# boundary conditions
PHYSICAL_GROUP AB BC u=0
PHYSICAL_GROUP CD BC v=0
PHYSICAL_GROUP BC BC p=10
FINO_STEP # solve problem
# write results
MESH_POST FILE_PATH le1-base.vtk VECTOR u v 0 sigmax sigmay tauxy
PRINT " u(D) = " %.9e u(2000,0) "mm" SEP " "
PRINT "σy(D) = " %.6f sigmay(2000,0) "MPa" SEP " "- the mesh created in the previous step is read with
MESH - the problem type is set with
FINO_PROBLEM(it has to be set after at leas one mesh was defined) - the (uniform) material properties are set as scalar variables
- the boundary conditions are set with
PHYSICAL_GROUPandBCusing the names defined in the.geofile - Fino is asked to solve the problem with
FINO_STEP - the resulting displacement vector \vec{u}(\vec{x}) and the stresses \sigma_x(\vec{x}), \sigma_y(\vec{x}) and \tau_{xy}(\vec{x}) are written in a VTK file with
MESH_POST(VTK needs three components for a vector so the third component is set identically to z@fig:ero) - the scalar results \sigma_y(2,0) is printed up to six decimal places of precision.
4 Execution
$ gmsh -2 le1-base.geo
Info : Running 'gmsh -2 le1-base.geo' [Gmsh 4.5.4, 1 node, max. 1 thread]
Info : Started on Tue Jun 2 17:34:22 2020
Info : Reading 'le1-base.geo'...
Info : Done reading 'le1-base.geo'
Info : Meshing 1D...
Info : [ 0 %] Meshing curve 1 (Line)
Info : [ 30 %] Meshing curve 2 (Ellipse)
Info : [ 50 %] Meshing curve 3 (Line)
Info : [ 80 %] Meshing curve 4 (Ellipse)
Info : Done meshing 1D (0.005673 s)
Info : Meshing 2D...
Info : Meshing surface 1 (Transfinite)
Info : Done meshing 2D (0.005954 s)
Info : Meshing order 2 (curvilinear on)...
Info : [ 0 %] Meshing curve 1 order 2
Info : [ 20 %] Meshing curve 2 order 2
Info : [ 40 %] Meshing curve 3 order 2
Info : [ 60 %] Meshing curve 4 order 2
Info : [ 80 %] Meshing surface 1 order 2
Info : Done meshing order 2 (0.334794 s)
Info : 14751 nodes 3876 elements
Info : Writing 'le1-base.msh'...
Info : Done writing 'le1-base.msh'
Info : Stopped on Tue Jun 2 17:34:22 2020
$ fino le1-base.fin
u(D) = -1.022155045e-01 mm
σy(D) = 92.691659 MPa
$ 5 Results
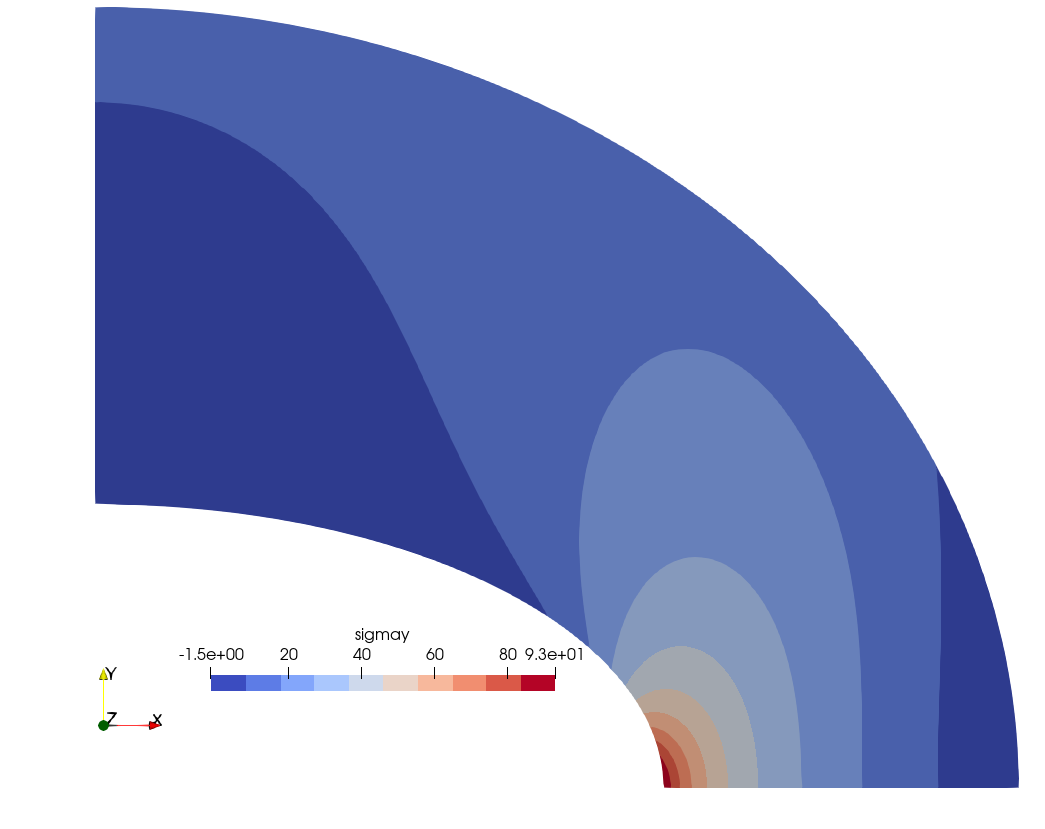
Fig. 3 shows the spatial distribution of \sigma_y as post-processed with ParaView. It can be seen how the stress are higher around the internal lower corner D.
5.1 Check
The value of \sigma_y(2,0) reported by Fino is “close” to the reference value of 92.7, but what does “close” mean? It is close enough? How accurate is this reference value? In sec. 6 we perform a parametric mesh convergence study, but another way to tackle these questions is to use Sparselizard’s automatic mesh capabilities.
Sparselizard is a user friendly finite element C++ library by Alexandre Halbach from University of Liege in Belgium. It is a fast, general, multiphysics, open source C++ finite element library running on GNU/Linux, Mac and Windows.
Indeed, the following routine solves the NAFEMS LE1 benchmark problem and asks for an automatic h refinement using the norm of the strain as the refinement criterion:
// NAFEMS LE1 Benchmark solved with Sparselizard with automatic mesh refinement
#include "sparselizardbase.h"
using namespace mathop;
void sparselizard(int order) {
int D = 4;
int AB = 5;
int BC = 6;
int CD = 7;
int bulk = 9;
double young = 210e3;
double poisson = 0.3;
double c1 = young/(1-poisson*poisson);
double c2 = poisson * c1;
mesh mymesh("le1-amr.msh", 0);
expression H(3,3,{c1, c2, 0,
c2, c1, 0,
0, 0, c1*0.5*(1-poisson)});
int i = 0;
do {
parameter E, nu;
field u("h1xy");
formulation elasticity;
E|bulk = young;
nu|bulk = poisson;
u.setorder(bulk, order);
u.compx().setconstraint(AB);
u.compy().setconstraint(CD);
elasticity += integral(bulk, predefinedelasticity(dof(u), tf(u), E, nu, "planestress"));
elasticity += integral(BC, +10.0*normal(BC)*tf(u));
solve(elasticity);
expression stress = H*strain(u);
field sigmay("h1");
sigmay.setorder(bulk, order);
sigmay.setvalue(bulk, comp(1, stress));
sigmay.write(bulk, "sigmay-amr-"+std::to_string(i)+".vtu", order);
printf("%d\t%.6f\t%.9e\n", i, sigmay.interpolate(bulk, {2000.0, 0.0, 0.0})[0], u.compx().interpolate(bulk, {2000.0, 0.0, 0.0})[0]);
mymesh.setadaptivity(norm(strain(u)), {}, 0, 5, 1e-5, 1e-5);
i++;
} while (mymesh.adapt());
}
int main(int argc, char **argv) {
SlepcInitialize(0,{},0,0);
sparselizard(2);
SlepcFinalize();
return 0;
}
The execution reveals that after six steps, the solution converges:
$ ./sparselizard
0 92.716163 -1.022044080e-01
1 92.678043 -1.022080927e-01
2 92.672615 -1.022083743e-01
3 92.676964 -1.022084134e-01
4 92.684052 -1.022084279e-01
5 92.691814 -1.022084353e-01
6 92.691814 -1.022084352e-01
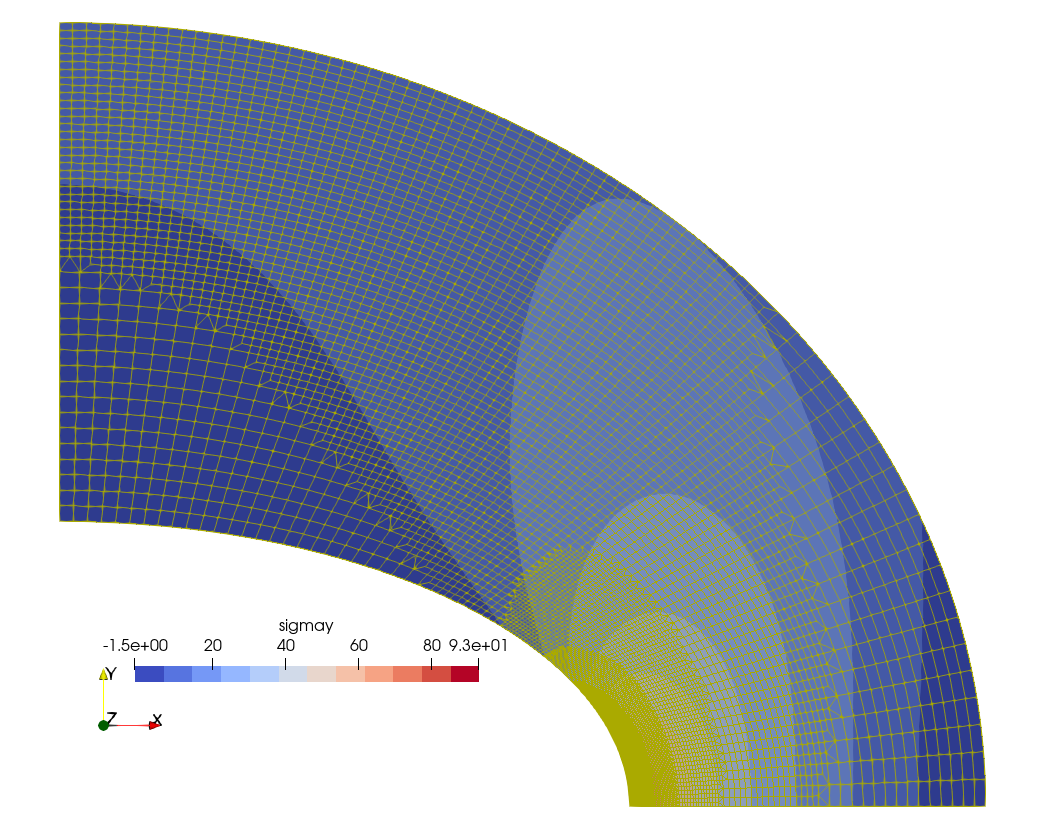
$ Indeed, fig. 4 shows how the mesh looks like in each of the refinement steps. Fig. 5 gives the final converged mesh and the resulting \sigma_y distribution. It should be noted that the initial mesh shown in fig. 4 (a) has a characteristic element length \ell_c 50% larger than the base mesh used by Fino in fig. 2.
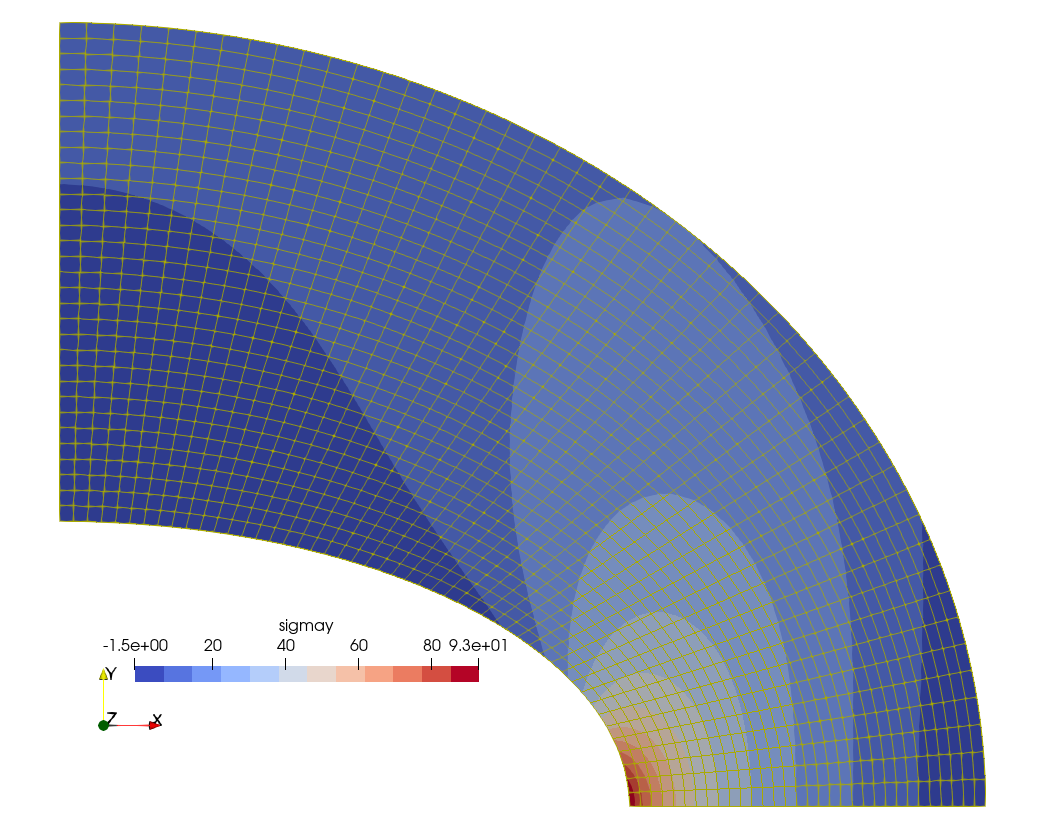
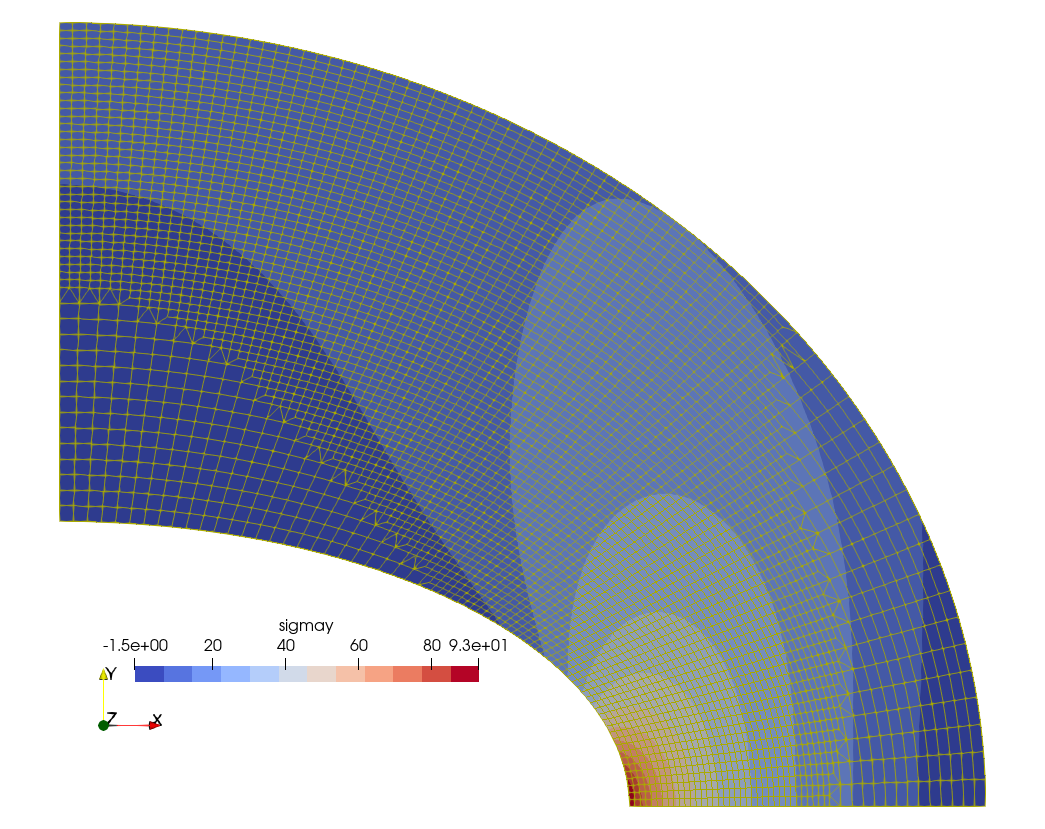
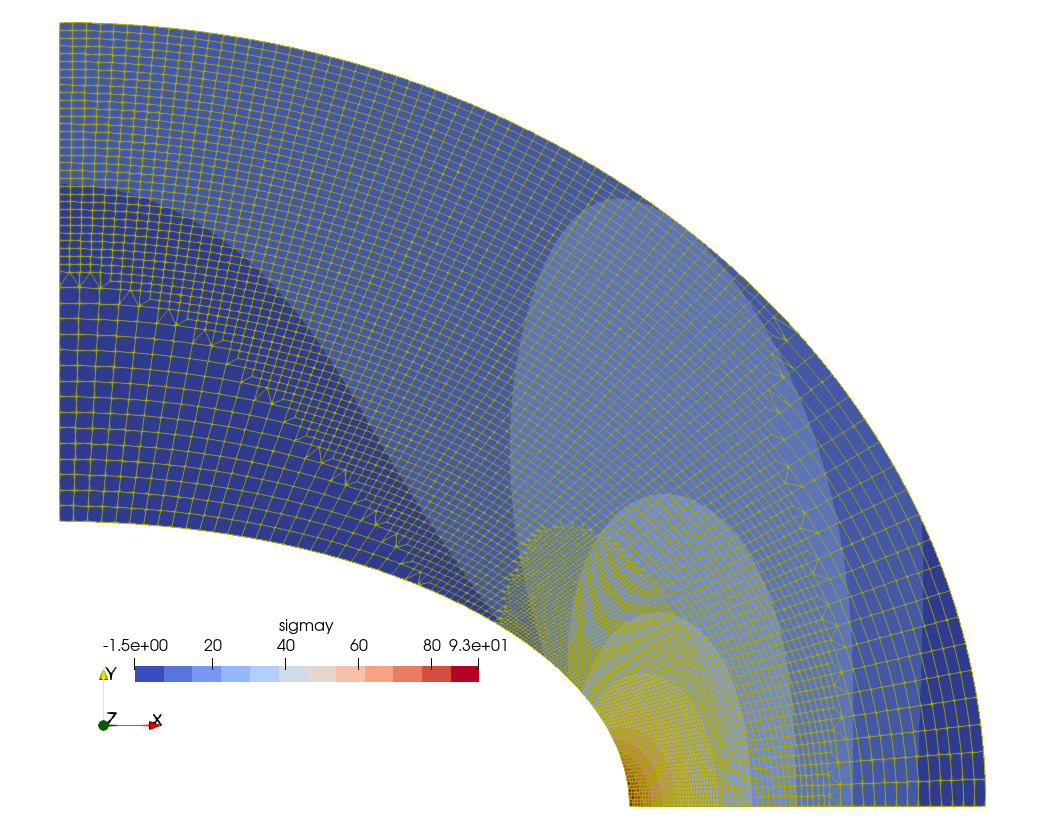
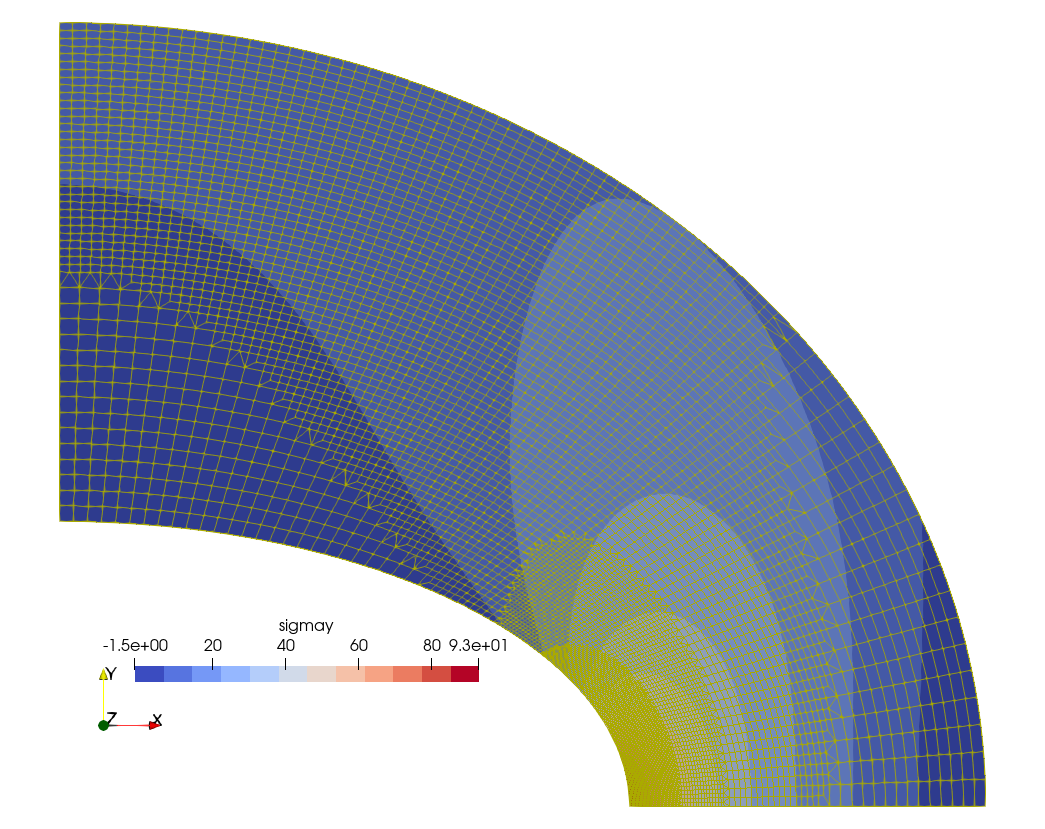
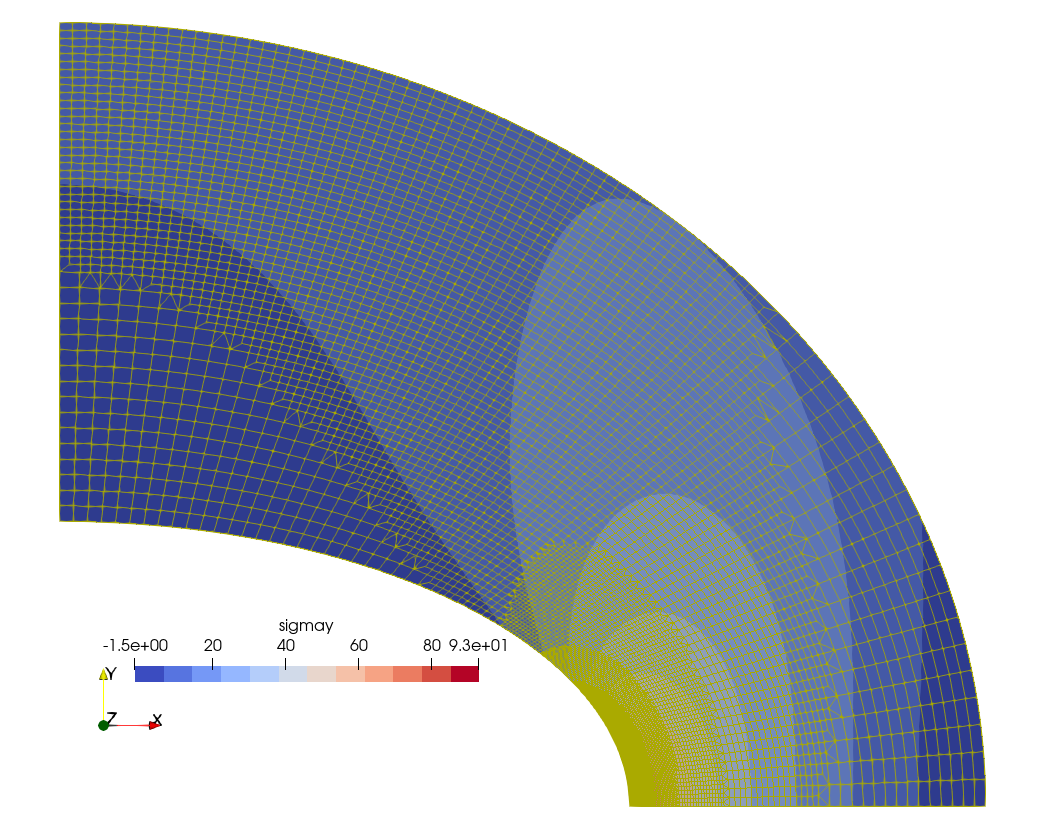
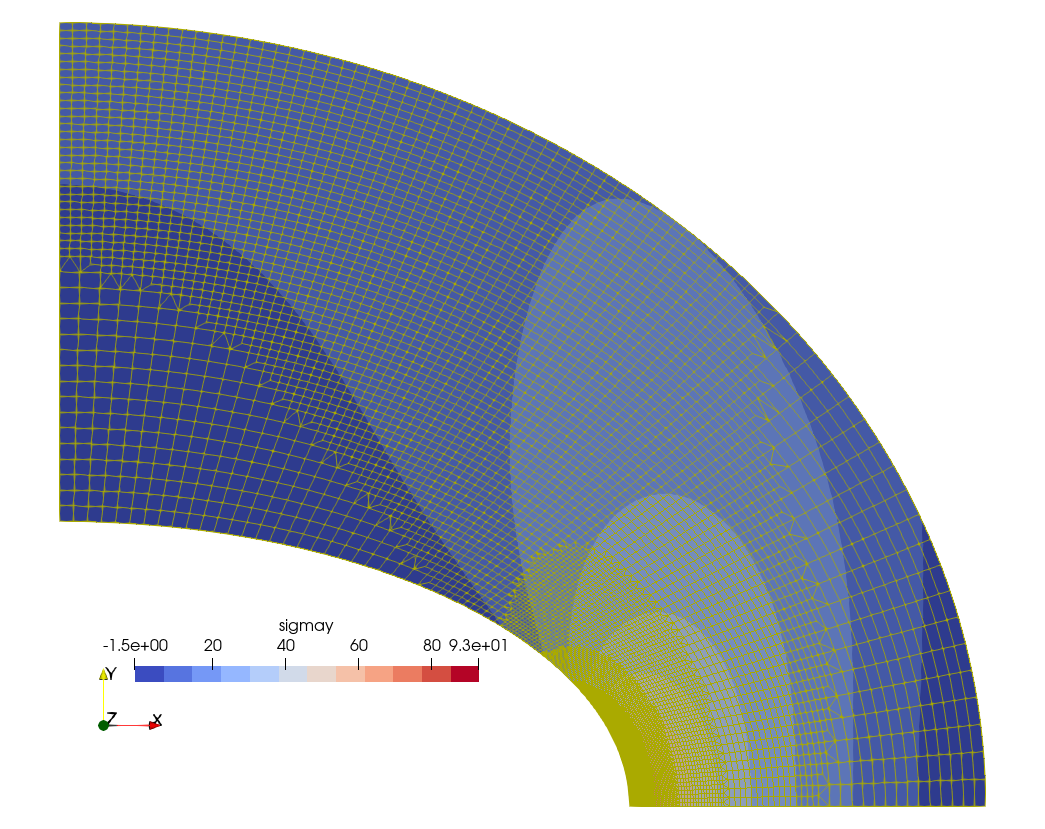
Figure 4: Automatic h-refinement steps by Sparselizard. a — Step 0, b — Step 1, c — Step 2, d — Step 3, e — Step 4, f — Step 5
6 Mesh convergence
To better understand the finite-element solutions of the NAFEMS LE1 problem, let us perform a parametric mesh convergence study. Not only should we vary (uniformly now) the element size but also the type and order. In particular we use the following element types:
- tri3
- tri6
- quad4
- quad8
- quad9
We now also allow unstructured grids so we can also try different meshing algorithms provided by Gmsh:
- delaunay
- frontal
- delquad
- packing
- structured
Figs. 6, 7 illustrate the topology of the unstructured grids used for the mesh convergence study for different element shapes and meshing algorithms. Figs. 8, 9 show the result of the convergence analysis by plotting \sigma_y(2,0) vs. the inverse number of nodes of the mesh for each element shape, order and algorithm. The “correct” answer to the problem is expected to be the extrapolation to 1/n \rightarrow 0 (i.e. n \rightarrow \infty). It can be seen, especially in fig. 9, that all the second-order results tend to converge to a stress which is slightly below the original reference value of 92.7 MPa—which nevertheless ought to be considered correct.
Figure 6: Unstructured triangular grids used in the mesh convergence study. a — Delaunay, b — Delquad, c — Frontal, d — Packing
Figure 7: Unstructured quadrangular grids used in the mesh convergence study. a — Delaunay, b — Delquad, c — Frontal, d — Packing
6.1 Comparison against Sparselizard
A similar mesh convergence study was performed with Sparselizard, comparing some of the previous results with was obtained by Fino. To avoid having to analyze too much data, only one unstructured algorithm (the Delaunay case) was used to compare the convergence rate with the structured case. Also, as Saprselizard does not support incomplete elements, eight-node quadrangles are not used. Figs. 10, 11 show the results with filled bullets for Fino and empty bullets for Sparselizard. The general trend is that everything converges to the expected showing that even though both codes give slightly different results, their numerical discretization is consistent, stable and thus convergent.