Fixed compressed cylinder
| Title | Fixed compressed cylinder |
| Tags | elasticity compression |
| Runnng time | a few minutes |
| See also | 006-cylinder-pure-compression |
| CAEplex case | https://caeplex.com/p/0585b |
| Available in | HTML PDF ePub |
1 Problem description
Let’s consider a cylinder whose base rests on the x-z plane centered at the origin. The cylinder has radius r=0.5~\text{mm} and height \ell=2~\text{mm} as in fig. 1 (a). The base is fully fixed (i.e. the three degrees of freedom are set to zero u=v=w=0) and the upper face has an uniform compressive pressure p=100~\text{MPa}. Young modulus is E=100~\text{GPa} and Poisson’s ratio is \nu=0.3. We want to address this problem as a full three-dimensional case, but first we solve it as an axially-symmetric geometry. Indeed, a r \times \ell rectangle in the x-y plane represents the cylinder as an axisymmetric problem (fig. 1 (b)).
Figure 1: A cylinder subject to a compressive pressure.. a — Continuous case, b — Full 3D cylinder and a 2D rectangle of size r \times \ell representing the axisymmetric case
1.1 Expected results and further considerations
The displacements and stresses distribution within the cylinder are to be obtained. This problem does not have an analytical solution and, even more, there is a stress singularity at the outer radius of the base. Yet, the deformed solution is expected to be like an (inverted) elephant(ish) foot shape, as the bottom is fully fixed and the compression pressure will force the material to displace radially since \nu \neq 0 .
The axisymmetric case is to be used as a reference solution, since the mesh can be fully structured and virtually infinitely refined. Once again, the full 3D case will be meshed using unstructured tetrahedra to avoid introducing biased orientations and to show that the results hold for arbitrary elements.
2 Parametric study
To know where we are in terms of mesh convergence, let’s first perform two parametric studies over the mesh size: one in the axi-symmetric case and one in the full 3D case. The parametric run is controlled by Fino (actually by wasora), and a new mesh is created for every step. First a .geo with the appropriate element size file out of a template is created out of a template and Gmsh is called from Fino before actually reading the .msh file.
On the one hand, there are some definitions that are common to the two problems so we put them in separate includible files lengths.fin and problem.fin (they cannot be merged into a single file because they need to be INCLUDEd from the main input at different locations):
E = 100e3 # [ MPa ]
nu = 0.3
PHYSICAL_GROUP NAME bottom BC fixed
PHYSICAL_GROUP NAME top BC ty=-100 # compression in y- [ Mpa ]
FINO_STEP
FINO_REACTION PHYSICAL_GROUP bottom RESULT ROn the other hand, the main input files for the two parametric runs are axi.fin and 3d.fin. They both include the common geometry lengths lengths.fin to have r and \ell as wasora variables (and then expand their values in the mesh template file) and the common problem definition problem.fin. First axi.fin
# illustration of the “elephant foot(ish)” effect when compressing a
# clamped solid cylinder in a 2d axi-symmetric case
# parametric run
INCLUDE lengths.fin
PARAMETRIC c MIN 25 MAX 200 STEP 25
lc = 1/c
FILE geo axi-%d.geo c
FILE msh axi-%d.msh c
FILE out axi-fino-%d.msh c
FILE vtk axi-fino-%d.vtk c
OUTPUT_FILE profile axi-fino-%d.dat c
M4 INPUT_FILE_PATH axi.geo.m4 OUTPUT_FILE geo EXPAND r EXPAND l EXPAND lc
SHELL "if [ ! -e axi-%g.msh ]\; then gmsh -v 0 -2 axi-%g.geo\; fi" c c
MESH FILE msh DIMENSIONS 2
FINO_PROBLEM AXISYMMETRIC SYMMETRY_AXIS y
INCLUDE problem.fin
PRINT c %.4f lc %g nodes %e u(0.95*r,0.05*l) v(0.95*r,0.05*l) %.10f strain_energy R(2)
MESH_POST FILE out VECTOR u v 0
MESH_POST FILE vtk VECTOR u v 0
u_r(y) := u(0.95*r, y)
PRINT_FUNCTION FILE profile FORMAT %e u_r MIN 0 MAX l NSTEPS 200and then 3d.fin:
# illustration of the “elephant foot(ish)” effect when
# compressing a clamped solid cylinder with full 3d
# parametric run
INCLUDE lengths.fin
PARAMETRIC c MIN 8 MAX 24 STEP 2
lc = 1/c
FILE geo 3d-%d.geo c
FILE msh 3d-%d.msh c
FILE out 3d-fino-%d.msh c
FILE vtk 3d-fino-%d.vtk c
OUTPUT_FILE profile 3d-fino-%d.dat c
M4 INPUT_FILE_PATH 3d.geo.m4 OUTPUT_FILE geo EXPAND r EXPAND l EXPAND lc
SHELL "if [ ! -e 3d-%g.msh ]\; then gmsh -v 0 -3 3d-%g.geo\; fi" c c
MESH FILE msh
FINO_PROBLEM ELASTIC
INCLUDE problem.fin
PRINT c %.4f lc %g nodes %e u(0.95*r,0.05*l,0) v(0.95*r,0.05*l,0) %.10f strain_energy R(2)
MESH_POST FILE out VECTOR u v w
MESH_POST FILE vtk VECTOR u v w
u_r(y) := u(0.95*r, y, 0)
PRINT_FUNCTION FILE profile FORMAT %e u_r MIN 0 MAX l NSTEPS 200These input files define a linear parametric range for variable c between particular limits and step sizes that depend on the problem type. They also define file names that include the value of the parameter c in their name and also compute the characteristic element size as \ell_c = 1/c. For instance, when c=10
- the geometry file is
axi-10.geo, - the mesh file is
axi-10.msh, - the output file is
axi-fino-10.msh, and - the element size is \ell_c = 0.1.
The M4 instruction, that calls the m4 macro processor, takes a template file (either axi.geo.m4 or 3d.geo.m4) and “fills in” the values of r, \ell and \ell_c so as to create an appropriate .geo input file for Gmsh, which is subsequently called if the mesh file for the current value of c does not exist.
In the axisymmetric case, a fully structured grid composed of second-order 9-node quadrangles (actually squares) is created. In the 3D case, fully unstructured second-order 10-node tetrahedra are used. The templates are axi.geo.m4
// an structured rectangle which creates an axi-symmetric
// solid cylinder of radius r and length (height) l
SetFactory("OpenCASCADE");
Rectangle(1) = {0, 0, 0, r, l};
// groups for BCs and volume
Physical Curve("bottom", 1) = {1};
Physical Curve("top", 2) = {3};
Physical Surface("bulk", 3) = {1};
// structured grid
Transfinite Line {1,3} = 1+r/lc;
Transfinite Line {2,4} = 1+l/lc;
Transfinite Surface "*";
Recombine Surface {1}; // quads instead of triangs
Mesh.ElementOrder = 2; // second-order quads
Mesh.SecondOrderIncomplete = 0; // force quads9 (if set to true, quad8 are created)and 3d.geo.m4
// a solid cylinder of radius r and length (height) l
// base is in xz, height is in z
SetFactory("OpenCASCADE");
Cylinder(1) = {0, 0, 0, 0, l, 0, r};
// groups for BCs and volume (surface)
Physical Surface("bottom", 1) = {3};
Physical Surface("top", 2) = {2};
Physical Volume("bulk", 3) = {1};
// unstructured grid
Mesh.CharacteristicLengthMax = lc;
Mesh.ElementOrder = 2;
Mesh.HighOrderOptimize = 2;The parametric runs write one line per each value of c in the standard output with the following columns
- the parameter c
- the characteristic element size \ell_c
- the number of nodes
- the horizontal displacement at the external radius and at one-twentieth of the height u(r,l/20)—u(r,l/20,0) in the 3D case
- the vertical displacement at the external radius and at one-twentieth of the height v(r,l/20)—v(r,l/20,0) in the 3D case
- the strain energy U
- the reaction force of the fixed base in the vertical direction R_y
3 Execution
$ fino axi.fin
25 0.0400 2525 8.257048e-05 -1.033879e-04 0.0775297616 78.5398225022
50 0.0200 10251 8.270061e-05 -1.035381e-04 0.0775344312 78.5395852629
75 0.0133 22575 8.274183e-05 -1.035790e-04 0.0775355966 78.5395730181
100 0.0100 40501 8.275715e-05 -1.035963e-04 0.0775360717 78.5395377296
125 0.0080 62625 8.276525e-05 -1.036059e-04 0.0775363746 78.5398046294
150 0.0067 89251 8.277084e-05 -1.036121e-04 0.0775365345 78.5395913328
175 0.0057 122325 8.277341e-05 -1.036161e-04 0.0775365533 78.5395179211
200 0.0050 161001 8.277645e-05 -1.036189e-04 0.0775367793 78.5399334485
$ fino 3d.fin
8 0.1250 6748 7.770105e-05 -1.004578e-04 0.0774786009 78.5392843913
10 0.1000 12534 8.066534e-05 -1.028128e-04 0.0774966605 78.5396002178
12 0.0833 20132 8.098786e-05 -1.027696e-04 0.0775040908 78.5396098622
14 0.0714 30716 8.087155e-05 -1.024939e-04 0.0775099236 78.5398409423
16 0.0625 45609 8.160801e-05 -1.026911e-04 0.0775145590 78.5397404081
18 0.0556 62788 8.207113e-05 -1.029076e-04 0.0775185989 78.5398045399
20 0.0500 85638 8.215427e-05 -1.029390e-04 0.0775208559 78.5399652975
22 0.0455 111761 8.233437e-05 -1.030996e-04 0.0775225793 78.5397878517
24 0.0417 143529 8.238272e-05 -1.032053e-04 0.0775246416 78.5398714217
$4 Results
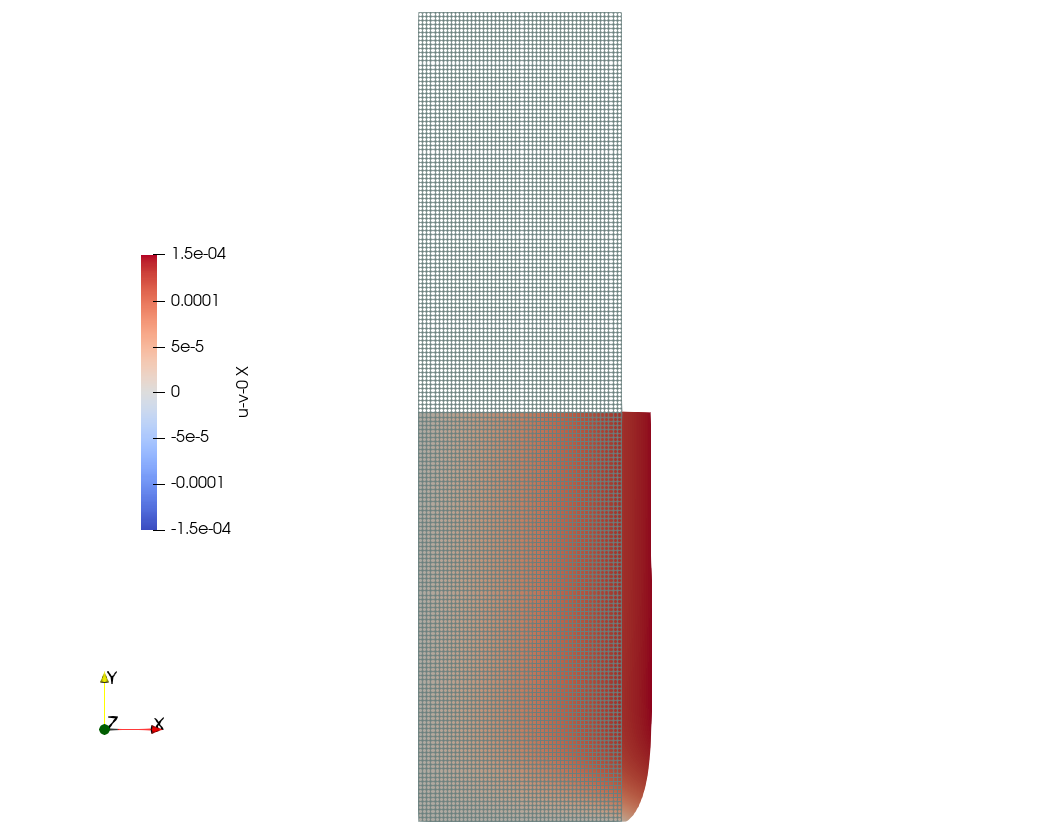
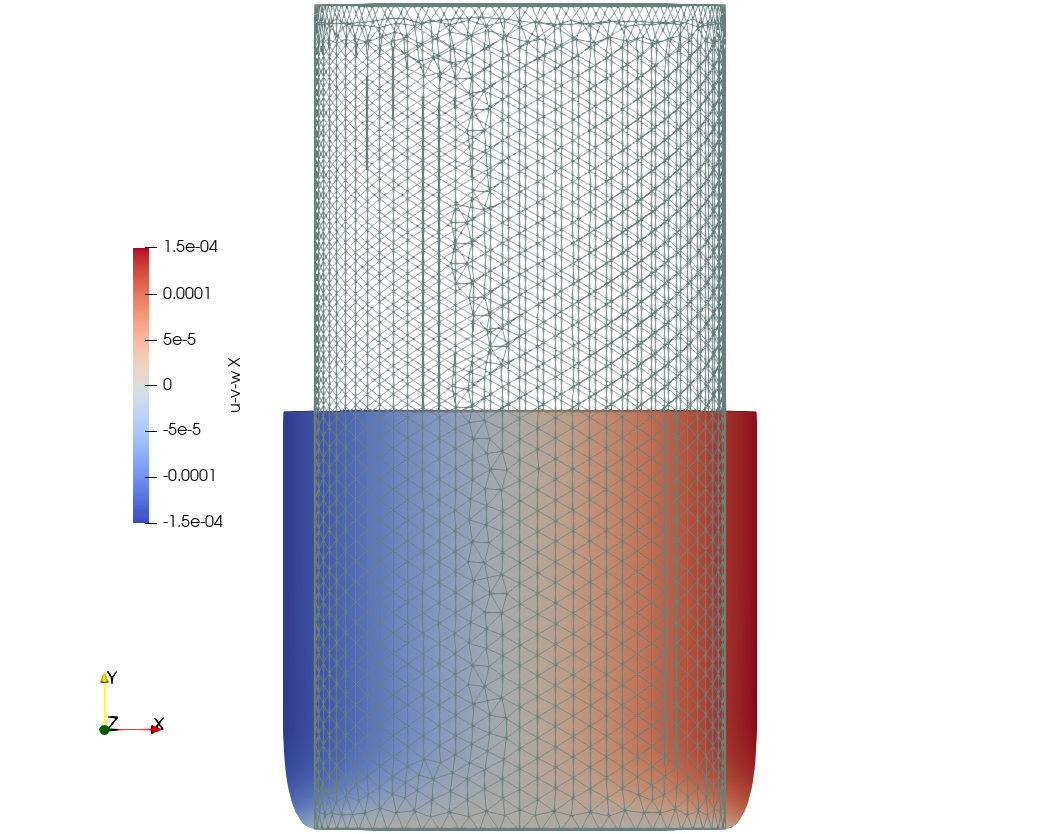
Figure 2: Displacements for both the axi-symmetric and three-dimensional cases.. a — Axi-symmetric results for c=100—40k nodes, b — Three-dimensional results for c=20—85k nodes
If we use a consistent and stable (and thus convergent due to the Lax Theorem) method, all the results obtained with an infinitely dense mesh ought to converge to the continuous solution. Of course, finite elements can only deal with a finite grid so parametric results on the number of unknowns are to be extrapolated up to infinite in order to estimate the converged values. As extrapolating to zero is easier than to \infty, the abscissa of the following plots use the inverse of the number of nodes—which in turn is a measure of the computational effort needed to solve the problem.
Figure 3: Energy and reaction force vs. number of nodes. a — Strain energy vs inverse of number of nodes, b — Vertical reaction force vs. inverse of number of nodes
Figure 4: Displacements vs. number of nodes. a — Horizontal displacement vs. inverse of number of nodes, b — Vertical displacement vs. inverse of number of nodes
4.1 Discussion
From figs. 3 (a), 3 (b), 4 (a), 4 (b) we can draw the following conclusions:
- All the axi-symmetric solutions seem to be converged within the mesh size range.
- The strain energy U in both cases approaches the theoretical converged value from below, which is what is expected as the problem is load-driven and the discretized problem is stiffer than the continuous one.
- The 3D results are consistent with the axi-symmetric ones for problems with more than approximately 25k nodes.
- The reaction R_y is far more accurate than the strain energy, displacements and stresses because it is computed so as to obtain global equilibrium exactly (up to the solver’s precision).
5 Check
So far we can verify that Fino gives the same result for the same problem solved either as a 2D axi-symmetric case and as a full three-dimensional problem. Since the compression of a fully-fixed cylinder does not have an analytical solution, we might need a little bit of validation against other programs to have an independent confirmation that Fino provides an accurate finite-element analysis.
In particular, we are going to check the profile of horizontal displacement u as a function of the coordinate y at a fixed radius x=0.95\cdot r. For the 3D case, we set z=0.
5.1 Sparselizard
Sparselizard is a user friendly finite element C++ library by Alexandre Halbach from University of Liege in Belgium. It is a fast, general, multiphysics, open source C++ finite element library running on GNU/Linux, Mac and Windows. It makes it very easy to solve hp-refined FEM problems with a few C++ function calls. Given the geographical closeness1 of course it reads Gmsh-generated meshes.
Sparselizard’s features are wide and varied, and elasticity is only one of the many problem types that it can solve. The full 3D case can be solved with this simple source file:
#include "sparselizardbase.h"
using namespace mathop;
void sparselizard(void) {
double y;
FILE *dat;
int bottom = 1, top = 2, bulk = 3; // numerical values of physical groups in the mesh
mesh mymesh("3d-lizard.msh"); // as in 3d-20.geo but converted to version 2.2
wallclock clk;
formulation elasticity;
field u("h1xyz");
u.setorder(bulk, 2);
u.setconstraint(bottom);
parameter E, nu;
E|bulk = 100e3; nu|bulk = 0.3;
elasticity += integral(bulk, predefinedelasticity(dof(u), tf(u), E, nu));
elasticity += integral(top, array1x3(0,-100,0)*tf(u));
solve(elasticity);
clk.print("Total calc time:");
dat = fopen ("lizard-3d.dat","w"); // write profile at x=0.95*r
for (y = 1e-2; y <= 2.0; y += 1e-2) {
fprintf(dat, "%g\t%e\n", y, abs(compx(u)).interpolate(bulk, {0.95*0.5, y, 0})[0]);
}
fclose(dat);
}
int main(void) {
SlepcInitialize(0,{},0,0);
sparselizard();
SlepcFinalize();
return 0;
}
The axi-symmetric case is essentially the same but it needs a call to setaxisymmetry() and obvious changes in the file names:
$ diff lizard-3d.cpp lizard-axi.cpp
9c9,10
< mesh mymesh("3d-lizard.msh");
---
> setaxisymmetry();
> mesh mymesh("axi-lizard.msh");
26c27
< dat = fopen ("lizard-3d.dat","w");
---
> dat = fopen ("lizard-axi.dat","w");
$The execution is (almost) silent and smooth:
$ make
[...]
$ ./run_sparselizard.sh
Loading mesh from file '3d-lizard.msh'
Extracted 85638 nodes
Extracted 74250 lines with curvature order 2
Extracted 122004 triangles with curvature order 2
Extracted 59141 tetrahedra with curvature order 2
Time to load the mesh:
393.984 ms
Total calc time:
47.5487 s
$As both programs, namely Fino and Sparselizard, are flexible enough to interpolate the data at arbitrary positions and to be able to write a one-dimensional profile out of the full 3D displacement fields, the comparison of the profiles obtained with each tool is rather easy by loading the data with Fino (or wasora):
FUNCTION u_fino(y) FILE_PATH 3d-fino-20.dat
FUNCTION u_lizard(y) FILE_PATH lizard-3d.dat
# write the two profiles and their differences
PRINT_FUNCTION FORMAT %e FILE_PATH diff-fino-lizard-3d.dat \
u_fino u_lizard u_lizard(y)-u_fino(y) (u_lizard(y)-u_fino(y))/u_lizard(y) \
MIN 2e-2 MAX 2 STEP 2e-2First, to check we are on the same page, the profiles are shown in fig. 5. Then, the actual absolute and relative difference between each case can be seen in figs. 6 (a), 6 (b).
Figure 6: Profile difference between Fino and Sparselizard for the same number of nodes.. a — Absolute difference, b — Relative difference
5.2 CalculiX
Let’s move on to solve the problem with CalculiX that, even though it does not share Fino’s design basis, at least it is free and open source2 and is a respected piece of software. Three 3D problems were solved both with CalculiX and with Fino using the same Gmsh-generated mesh in each case as shown in tbl. 1.
| Case | \ell_c [mm] | CalculiX input | CalculiX output |
|---|---|---|---|
| 10k | 0.10 | ccx-10k.inp | ccx-10k.frd |
| 20k | 0.08 | ccx-20k.inp | ccx-20k.frd |
| 80k | 0.05 | ccx-80k.inp | ccx-80k.frd |
After creating the three input files from FreeCAD FEM workbench manually in a point-and-clicky non-script-friendly way3 (i.e. quite orthogonal to the UNIX philosophy that Fino follows), we can finally let our internal hacker out by running ccx from a shell for loop. Yet, the rule of silence is a total stranger to CalculiX so we need to forward the unneeded output to Dave Null. And in the mean time, we can time(1) the execution.
$ for i in 10 20 80; do echo $i; time ccx ccx-${i}k > /dev/null; done
10
real 0m3.660s
user 0m3.804s
sys 0m0.391s
20
real 0m11.581s
user 0m11.665s
sys 0m0.420s
80
real 2m31.016s
user 2m30.553s
sys 0m0.996s
$The Fino counterpart, which actually illustrates the difference between the spirit and the basis of both codes, is composed of two files for all the three (which could be far more if CalculiX was script-friendlier) cases. First, a template fino-ccx.geo.m4 for the mesh with only one expandable macro, namely the characteristic length \ell_c:
Merge "Cylinder_Geometry.brep"; // read the cylinder from a BREP as in the CalculiX case
Physical Surface("bottom") = {3};
Physical Surface("top") = {2};
Physical Volume("bulk") = {1};
Mesh.CharacteristicLengthMax = lc;
Mesh.CharacteristicLengthMin = 0.0;
Mesh.Optimize = 1;
Mesh.OptimizeNetgen = 1;
Mesh.HighOrderOptimize = 1;
Mesh.ElementOrder = 2;
Mesh.Algorithm = 6;
Mesh.Algorithm3D = 1;
Secondly, the actual input file fino-ccx.fin that accepts the case number as a parameter from the command line and call Gmsh if needed:
INCLUDE lengths.fin
# choose appropriate lc according to command-line argument
lc = if($1=10, 0.1, if($1=20, 0.08, 0.05))
# expand template and call gmsh if needed
M4 INPUT_FILE_PATH fino-ccx.geo.m4 OUTPUT_FILE_PATH fino-ccx-$1k.geo EXPAND lc
SHELL "if [ ! -e fino-ccx-$1k.msh ]\; then gmsh -v 0 -3 fino-ccx-$1k.geo\; fi"
# read mesh and solve problem
MESH FILE_PATH fino-ccx-$1k.msh
INCLUDE problem.fin
# extract horizontal displacement at 95% of r
u_r(y) := u(0.95*r, y, 0)
# write the profile in a file
PRINT_FUNCTION FILE_PATH fino-ccx-$1k.dat FORMAT %e u_r MIN 0 MAX l NSTEPS 200
# tell the world how much time we spent
PRINT "total run time for $1k:" %.3g time_wall_total "seconds"The three Fino cases can be run all at once with a similar (yet cleaner) shell loop:4
$ for i in 10 20 80; do fino fino-ccx.fin $i; done
total run time for 10k: 2.35 seconds
total run time for 20k: 4.38 seconds
total run time for 80k: 19.4 seconds
$Now we can read back each of the three CalculiX outputs in its FRD format, extract the profile u(0.95\cdot r,y,0) and compare it to Fino’s. For that end, we use the following input file diff-fino-ccx.was which, again, can be run by either Fino or its base framework wasora, that is able to read multidimensional point-wise functions defined in either .msh, .vtk or .frd files and interpolate them back at any arbitrary location x,y,z of space:
# read Fino’s 3D profile
FUNCTION u_fino(y) FILE_PATH fino-ccx-$1k.dat
# read CalculiX output in its F77-based own format FRD
MESH FILE_PATH ccx-$1k.frd DIMENSIONS 3 READ_SCALAR D1 AS u_ccx_frd
# extract the profile at 95% of the radius
u_ccx(y) := u_ccx_frd(0.95*0.5, y, 0)
# write the two profiles and their differences
PRINT_FUNCTION FORMAT %e FILE_PATH diff-fino-ccx-$1k.dat \
u_fino u_ccx u_ccx(y)-u_fino(y) (u_ccx(y)-u_fino(y))/u_ccx(y) \
MIN 1e-2 MAX 2 NSTEPS 100$ for i in 10 20 80; do wasora diff-fino-ccx.was $i; done
$Figure 7: Profile difference between Fino and CalculiX for the same number of nodes.. a — Absolute difference, b — Relative difference
5.3 NASTRAN
Let’s now compare Fino to NASTRAN. Whilst the usable version is neither free nor open source, NASA has released a now 25-years old version under an open-source agreement.5 Even though the source is available, the software is not free as the license has some requirements which are incompatible with software freedom and there are no instructions nor makefiles to compile the code (yet there are a few forks that do). There is a Debian package, but it is tagged as non-free and depends on unmaintained libraries. In any case, NASTRAN has has been in the scene for almost sixty years now.
M3D FEA’s founder Roy Blows has provided the result of the fixed compressed cylinder using an axi-symmetric grid composed of structured second-order triangles with exactly 1701 nodes. Setting c=20 in Fino’s axi-symmetric case above and not recombining the triangles leads Gmsh to create exactly the same grid.
Figure 8: Axi-symmetric meshes with 1701 nodes each. a — NASTRAN, b — Fino/Gmsh
Roy’s mesh and results stored in axi.f06, a paginated6 ASCII text file that was manually converted to Gmsh’s .msh v2.27 file format which Fino/wasora can then read back and operate on:
# read Fino’s profile
FUNCTION u_fino(y) FILE_PATH fino-nastran.dat
# read NASTRAN’s output (manually) converted to Gmsh format
MESH FILE_PATH nastran.msh DIMENSIONS 2 READ_SCALAR u AS u_nastran_msh
# extract profile minding the units
u_nastran(y) := 1e3*u_nastran_msh(1e-3*0.95*0.5, 1e-3*y)
# write the two profiles and their differences
PRINT_FUNCTION FORMAT %e FILE_PATH diff-fino-nastran.dat \
u_fino u_nastran u_nastran(y)-u_fino(y) (u_nastran(y)-u_fino(y))/u_nastran(y) \
MIN 2e-2 MAX 2 NSTEPS 100Figure 9: Profile difference between Fino and NASTRAN for the same number of nodes.. a — Absolute difference, b — Relative difference
5.4 ANSYS
Nick Stevens has solved the full 3D case with ANSYS and provided plain-text results. After some manipulation—that involved amongst other issues, having to figure out ANSYS own node ordering for 20-nodes-hexahedra—the displacements were written, again, in Gmsh’s .msh v2.2, ready to be read back by wasora and compared to Fino’s.
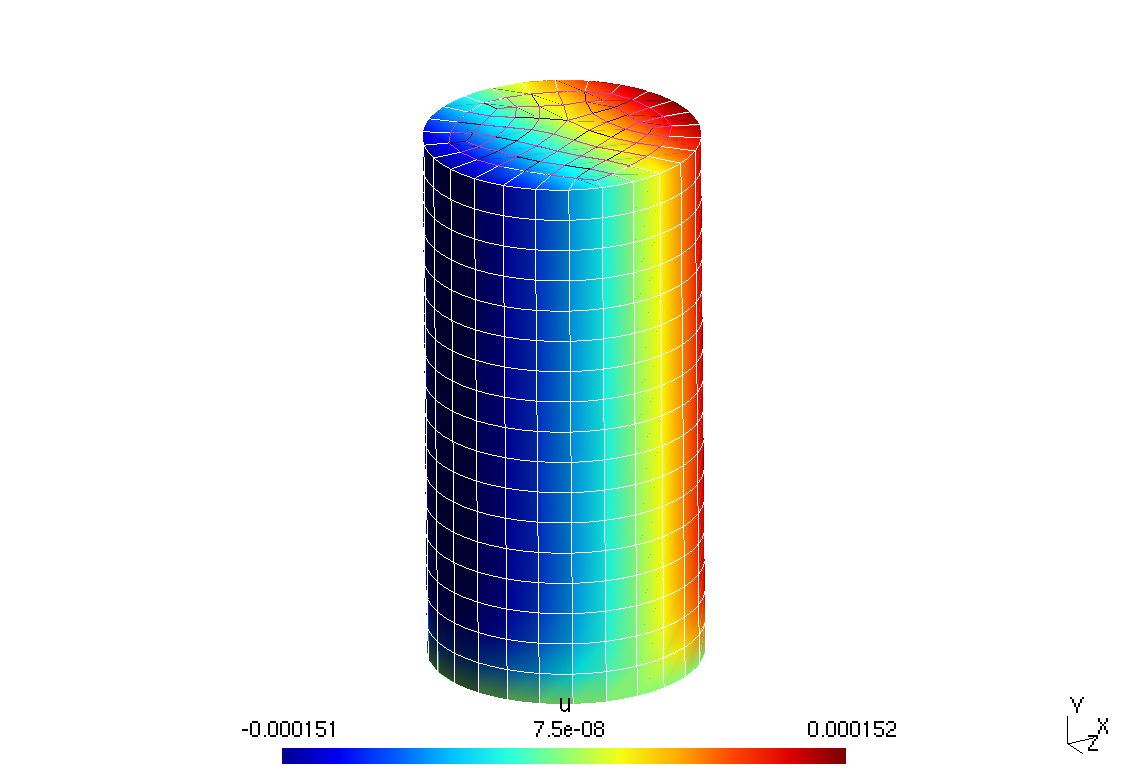
The horizontal displacement distribution can be compared to Fino’s 3D solution above with c=8 which results in 6.7k nodes—yet the elements are 10-noded tetrahedra as illustrated in fig. 10. The comparison is shown in fig. 11.
FUNCTION u_fino(y) FILE_PATH 3d-fino-8.dat
MESH FILE_PATH ansys.msh DIMENSIONS 3 READ_SCALAR u AS u_ansys_msh
u_ansys(y) := u_ansys_msh(0.95*0.5, y, 0)
PRINT_FUNCTION FORMAT %e FILE_PATH diff-fino-ansys.dat \
u_fino u_ansys u_ansys(y)-u_fino(y) (u_ansys(y)-u_fino(y))/u_ansys(y) \
MIN 1e-2 MAX 2 NSTEPS 100Figure 11: Profile difference between Fino and ANSYS for the same number of nodes.. a — Absolute difference, b — Relative difference
Dr. Christophe Geuzaine, Gmsh’s main developer, was Alexandre Halbach’s PhD thesis advisor↩︎
At least theoretically although in practice the source is in a mixture of Fortran 77 and Fortranish-C that is closer to a binary object file than to actual human-understandable source code.↩︎
Good luck tracking changes in the
ccx-*.inpinput files with Git.↩︎The difference in the execution times (on the very same machine) is out of the scope of the present discussion.↩︎
The code seems to be from 1995 but the manual is from 1986.↩︎
As in the 1970s where every fifty-something lines a header with the current date and capitalized table captions explaining what each column is, as if the results are expected to be printed in a dot-matrix printer in 2020.↩︎
The rationale behind using legacy version 2.2 and not the latest 4.1 is that the former is easier to edit and modify directly, not because Fino cannot understand the latter.↩︎