Heat conduction
FeenoX Tutorial #3
Table of contents
1 Foreword
Welcome to FeenoX’s tutorial number three. Here you will learn how to solve the heat conduction equation with FeenoX in all of its flavors:
- linear and non-linear,
- static and transient.
All the files needed to go through the tutorial are available in FeenoX’s
Git repository under doc/tutorials/320-thermal. Make
sure you also check the heat
conduction examples.
Heads up: this tutorial is quite long. For a quicker introduction, check out the thermal annotated examples in FeenoX webpage.
1.1 Summary
We start solving linear steady-state problems. As long as neither of the
- material properties, nor
- sources
depend on the temperature T(\mathbf{x}) and
- the boundary conditions do not depend or depend linearly on T(\mathbf{x})
then problem is linear. If these three guys depend on space \mathbf{x} (but not on T(\mathbf{x})), the problem is still linear no matter how complex it looks like. The following problem (whose output should be a small number, which is a “error” measure) discussed in sec. 2.5 is still linear:
PROBLEM thermal 2D READ_MESH square.msh # manufactured solution T_manufactured(x,y) = 1 + sin(2*x)^2 * cos(3*y)^2 # conductivity k(x,y) = 1 + x - y/2 # heat source needed to get the manufactured solution VAR x' x'' y' y'' q(x,y) = -(derivative(k(x',y) * derivative(T_manufactured(x'',y), x'', x'), x', x) + \ derivative(k(x,y') * derivative(T_manufactured(x,y''), y'', y'), y', y)) # boundary conditions, two fixed temps and two heat fluxes BC left T=T_manufactured(x,y) BC top T=T_manufactured(x,y) BC bottom q=+(-k(x,y)*derivative(T_manufactured(x,y'),y',y)) BC right q=-(-k(x,y)*derivative(T_manufactured(x',y),x',x)) SOLVE_PROBLEM WRITE_MESH manufactured.vtk T T_manufactured T(x,y)-T_manufactured(x,y) # compute and show L-2 error INTEGRATE (T(x,y)-T_manufactured(x,y))^2 RESULT e2 PRINT e2If these conditions are not met, then the problem is non-linear. FeenoX is able to detect this and will automatically switch to a non-linear solver. Why would the user need to tell the solver if the problem is linear or not, as in most FEA tools? If you think it through, it should be the other way round. And that is what FeenoX does.
Non-linearities can be triggered by either
- setting a boundary condition that depends non-linearly on T(\mathbf{x}), such as radiation, and/or
- having a conductivity that depends on temperature, which is the case for most materials anyway, and/or
- using a heat source that is temperature-dependent, where increasing T decreases the source.
We can check if FeenoX can detect the non-linearities by using the advanced options
--snes_monitorand/or--snes_viewin the command line. Here, SNES means “Scalable Non-linear Equation Solvers” in PETSc’s jargon. The--snes_viewoption shows some details about the solver. In linear problems, SNES is not used but the KSP (Krylov SubSpace solvers) framework is used instead. Therefore, if we used--snes_viewin a linear problem then FeenoX would complain about an unused command-line option.Heads up: these are advanced options. If you did not understand the paragraph above, do not worry. You are still good to go.
If, for some reason, the user does not want to have FeenoX to auto-detect the non-linearities then she could force the problem type using either
- the keywords
LINEARandNON_LINEARin thePROBLEMdefinition, or - the command-line
options
--linearand--non-linear.
- the keywords
Different linear and non-linear solvers (and pre-conditioners) can be chosen either from the command line (e.g.
--snes_type=newtonls) or from thePROBLEMdefinition (e.g.NONLINEAR_SOLVER newtonls). Check out the FeenoX manual section for the keywordPROBLEMfor further details. FeenoX can have hard-coded PETSc options using thePETSC_OPTIONSdefinition as well.Heads up: again, do not worry.
Finally we show how to solve transient problems. Transients are triggered by setting the special variable
end_timeto a positive value.FeenoX uses PETSc’s TS framework for transient problems. Different schemes can be chosen either from the command line (e.g.
--ts_type=bdf) or from thePROBLEMdefinition (e.g.TRANSIENT_SOLVER bdf).We solve transient problems either
- starting from an arbitrary initial temperature distribution using constant boundary conditions
- starting from a steady-state solution and changing the boundary conditions over time
- both
If the initial condition does not satisfy the fixed temperature conditions, the solver will not converge. But we can be smart and use FeenoX’s functions like
limit,if,min,max, etc. to satisfy them at t=0 and then quickly take the boundary conditions to their actual value.
2 Linear steady-state problems
In this section we are going to ask FeenoX to compute a temperature distribution T(\mathbf{x}) that satisfies the linear heat conduction equation
- \text{div} \Big[ k(\mathbf{x}) \cdot \text{grad} \left[ T(\mathbf{x}) \right] \Big] = q(\mathbf{x}) \qquad{(1)}
along with proper boundary conditions.
2.1 Temperature conditions
The simplest heat conduction problem involves a slab geometry with prescribed temperatures at both ends. If the conductivity k is uniform, then the solution is a linear interpolation of these two temperatures. Hence, the solution is independent of the actual value of the conductivity, provided it is uniform.
2.1.1 Single-material slab
Let us create a unitary slab between x=0 and x=1
with Gmsh using this slab.geo:
Point(1) = {0, 0, 0};
Point(2) = {1, 0, 0};
Line(1) = {1, 2};
Physical Point("left") = {1};
Physical Point("right") = {2};
Physical Line("bulk") = {1};
Transfinite Curve {1} = 10+1; // 11 nodes = 10 elementsThe end at x=0 is called
left and the one at x=1 is
called right. So we can ask FeenoX to solve a thermal
problem with uniform conductivity k and
fixed temperatures at both ends by
Defining
PROBLEMasthermaland giving either1dorDIM 1:PROBLEM thermal 1dNote: you can check which problems FeenoX can solve by running it with
--pdes:$ feenox --pdes laplace mechanical modal neutron_diffusion neutron_sn thermal $Setting the special variable
kto a constant:k = 1The fact that the conductivity is given as a variable means that
- there is a single material, and
- its conductivity is uniform, i.e. it does not depend on space.
but it can eventually depend on time, as discussed in sec. 4.
Giving
Tequal to the desired temperature values after theBCdefinition for bothleftandrightBC left T=0 BC right T=1Recall that the names
leftandrightcome from the names of the physical groups in the.mshfile read by FeenoX (which in turn were defined in the.geo).
After the instruction SOLVE_PROBLEM
is executed, the solution T(x) is
available as the one-dimensional
function T(x). We can then
- print its definition values with
PRINT_FUNCTION, and/or - evaluate it at any arbitrary location x (or
xin the input file). FeenoX will use the shape functions to interpolate the nodal solutions.
Here’s a working input file slab-uniform.fee:
# ask to solve a thermal problem
PROBLEM thermal 1d
# read the mesh
READ_MESH slab.msh
# conductivity: given as a the k variable means uniform single-material
k = 1
# boundary conditions: T=something means "fixed temperature"
BC left T=0
BC right T=1
SOLVE_PROBLEM
# the solution is available as the function T(x), which we can
# i. print its definition values
PRINT_FUNCTION T
# ii. evaluate it at any arbitrary location `x`
PRINT "\# the temperature at x=2/3 is" T(2/3) We can run it to get the requested results:
$ gmsh -1 slab.geo
Info : Running 'gmsh -1 slab.geo' [Gmsh 4.11.0-git-e8fe6f6a2, 1 node, max. 1 thread]
Info : Started on Sat Dec 2 14:12:31 2023
Info : Reading 'slab.geo'...
Info : Done reading 'slab.geo'
Info : Meshing 1D...
Info : Meshing curve 1 (Line)
Info : Done meshing 1D (Wall 0.000329053s, CPU 0.00022s)
Info : 11 nodes 12 elements
Info : Writing 'slab.msh'...
Info : Done writing 'slab.msh'
Info : Stopped on Sat Dec 2 14:12:31 2023 (From start: Wall 0.00535225s, CPU 0.020205s)
$ feenox slab-uniform.fee
0 0
1 1
0.1 0.1
0.2 0.2
0.3 0.3
0.4 0.4
0.5 0.5
0.6 0.6
0.7 0.7
0.8 0.8
0.9 0.9
# the temperature at x=2/3 is 0.666667Homework
- Check that the solution does not depend on k.
- Change the values of the boundary conditions and check the result is always a linear interpolation.
- Why does the hash
#need to be escaped in the
2.1.2 Two-material slab
If we have two (or more) materials, there are two ways to give their properties:
- Using the
MATERIALkeyword, or - Appending
_groupnameto either a variable or a function of space.
For example, let us now create a geometry where the left half of the slab (x<0.5) is made of metal (i.e. high conductivity k=9) and the right half of the slab (x>0.5) is made of plastic (i.e. low conductivity k=1):
Point(1) = {0.0, 0, 0};
Point(2) = {0.5, 0, 0};
Point(3) = {1.0, 0, 0};
Line(1) = {1, 2};
Line(2) = {2, 3};
Physical Point("left") = {1};
Physical Point("right") = {3};
Physical Line("metal") = {1};
Physical Line("plastic") = {2};
Transfinite Curve {1,2} = 5+1;We now have two “volumetric” labels metal and
plastic. The first way to give the conductivities is with
the MATERIAL
keyword, one for each material:
PROBLEM thermal 1d
READ_MESH metal-plastic-slab.msh
MATERIAL metal k=9
MATERIAL plastic k=1
BC left T=0
BC right T=1
SOLVE_PROBLEM
PRINT_FUNCTION T
PRINT "\# the temperature at x=1/2 is" T(1/2) The other way is to use two variables, namely k_metal
and k_plastic:
PROBLEM thermal 1d
READ_MESH metal-plastic-slab.msh
k_metal=9
k_plastic=1
BC left T=0
BC right T=1
SOLVE_PROBLEM
PRINT_FUNCTION T
PRINT "\# the temperature at x=1/2 is" T(1/2) $ feenox metal-plastic-vars.fee | tee vars.txt
0 0
0.5 0.1
1 1
0.1 0.02
0.2 0.04
0.3 0.06
0.4 0.08
0.6 0.28
0.7 0.46
0.8 0.64
0.9 0.82
# the temperature at x=1/2 is 0.1
$ feenox metal-plastic-material.fee > material.txt
$ diff vars.txt material.txt
$ 2.2 Heat flux conditions
Let us now investigate another boundary condition, namely setting a
heat flux condition. Going back to the single-material one-dimensional
slab, let us keep T(x=0)=0 but set
q'(x=1)=1. We can check if the heat
flux at the other side left (i.e. where we fixed the
temperature) is equal in magnitude and opposite in sign to the
prescribed heat flux at right with the COMPUTE_REACTION
instruction:
PROBLEM thermal 1d
READ_MESH slab.msh
k = 1
# boundary conditions: q=something means "prescribed heat flux"
BC left T=0
BC right q=1
SOLVE_PROBLEM
PRINT_FUNCTION T
COMPUTE_REACTION left RESULT q_left
PRINTF "\# the heatflux at left is %g" q_left$ feenox slab-uniform-heatflux.fee
0 0
1 1
0.1 0.0999997
0.2 0.2
0.3 0.3
0.4 0.4
0.5 0.5
0.6 0.6
0.7 0.7
0.8 0.8
0.9 0.9
# the heatflux at left is -0.999997
$ Let us now introduce a non-uniform conductivity depending on space as
k(x) = 1+x
and set the heat flux to 1/\log(2). This problem has the analytical solution
T(x) = \frac{\log(1+x)}{\log(2)}
which we can check with PRINT_FUNCTION.
Since we have only one material, we can define a function
k(x) to define the space-dependent property:
PROBLEM thermal 1d
READ_MESH slab.msh
k(x) = 1+x
BC left T=0
BC right q=1/log(2)
# define a function with the analytical solution
error(x) = T(x)-log(1+x)/log(2)
SOLVE_PROBLEM
# without an explicit range the definition points are written
PRINT_FUNCTION T error
# since error is algebraic we have to give an explicit range
PRINT_FUNCTION error MIN 0 MAX 1 STEP 1e-2 FILE slab-kofx-error.dat$ feenox slab-kofx-heatflux.fee | sort -g | tee slab-kofx-heatflux.dat
0 0 0
0.1 0.137399 -0.000104342
0.2 0.262851 -0.000183236
0.3 0.378267 -0.000244866
0.4 0.485133 -0.000293832
0.5 0.58463 -0.000332899
0.6 0.677707 -0.000365263
0.7 0.765143 -0.000392187
0.8 0.847582 -0.000414528
0.9 0.925566 -0.000433506
1 0.99955 -0.000449861
$ pyxplot slab-kofx-heatflux.ppl
$ Figure 1: Output of slab-kofx-heatflux.fee.
a — Computed temperature, b — Error
Homework
- Verify that T(x) = \frac{\log(1+x)}{\log(2)} is a solution of the differential equation and satisfies the boundary conditions.
- Rewrite the space-dependent conductivity k(x)=1+x using the
MATERIALkeyword.
2.3 Convection conditions
To define a convection condition we need to pass two parameters to
the BC keyword:
- A convection coefficient
h - A reference temperature
Tref
For instance
BC right h=100+y Tref=2000To illustrate this feature, let us solve heat conduction on the Stanford Bunny with
- A fixed space-dependent temperature in the base
- A convection condition on the rest of the external surface where the coefficient h varies linearly with the vertical z coordinate
PROBLEM thermal 3d
# https://upload.wikimedia.org/wikipedia/commons/4/43/Stanford_Bunny.stl
READ_MESH bunny.msh SCALE 1e-3
PHYSICAL_GROUP bunny DIM 3 # this is to compute the COG
# uniform conductivity
k = 25
# base with a prescribed space-dependent temperature
BC base T=250-2e3*sqrt((x-bunny_cog[1])^2+(y-bunny_cog[2])^2)
# rest with a convection condition
BC rest h=10+50*(z-bunny_cog[3]) Tref=100
SOLVE_PROBLEM
WRITE_RESULTS FORMAT vtk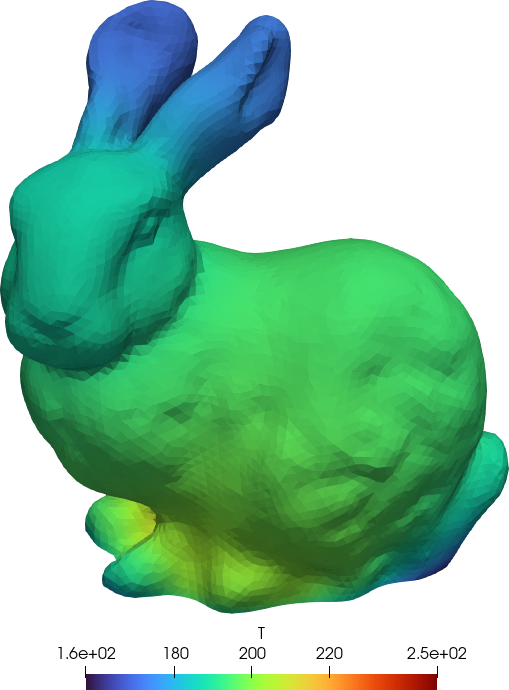
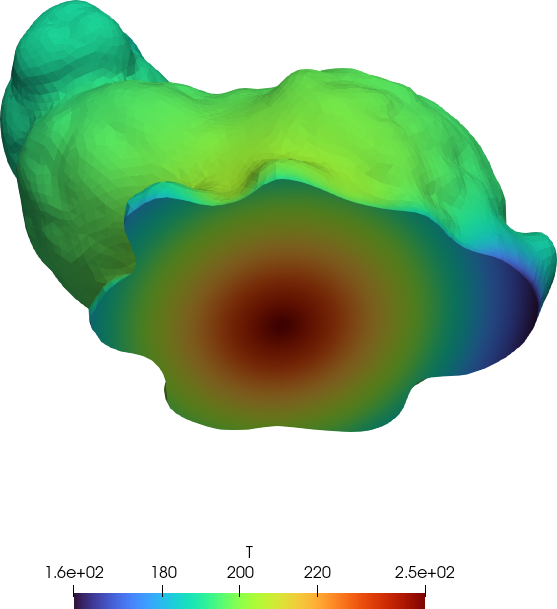

Figure 2: Output of bunny-thermal.fee.
2.4 Volumetric heat sources
So far all the sources of heat came from boundary conditions. Let us now define volumetric heat sources, that is to say, heat which is generated within the bulk of the materials like electrical, chemical or fission heating.
To do so, we can use the property
q which works exactly like the conductivity
k. Even more, it works like any other material
property:
- If there is only one material, it can be defined either as a
variable
qor a functionq(x,y,z) - If there are many materials, it can be defined either
- within the
MATERIALkeyword, or - by defining a variable or function named
q_groupname, one for each volumetric group in the mesh
- within the
Consider the unit square [0,1]\times[0,1]:
SetFactory("OpenCASCADE");
Rectangle(1) = {0, 0, 0, 1, 1, 0};
Physical Surface("bulk", 1) = {1};
Physical Curve("left", 2) = {4};
Physical Curve("right", 3) = {2};
Physical Curve("bottom", 4) = {1};
Physical Curve("top", 5) = {3};
Mesh.MeshSizeMax = 1/10;
Let us set
- uniform unitary conductivity k
- uniform unitary power source q
- T=0 at the four edges
Note that since there are four different groups holding the same
boundary condition we can use the GROUP keyword in BC
to apply the same condition to more than one physical group:
PROBLEM thermal 2D
READ_MESH square.msh
k = 1
q = 1
BC left T=0 GROUP right GROUP bottom GROUP top
SOLVE_PROBLEM
WRITE_RESULTS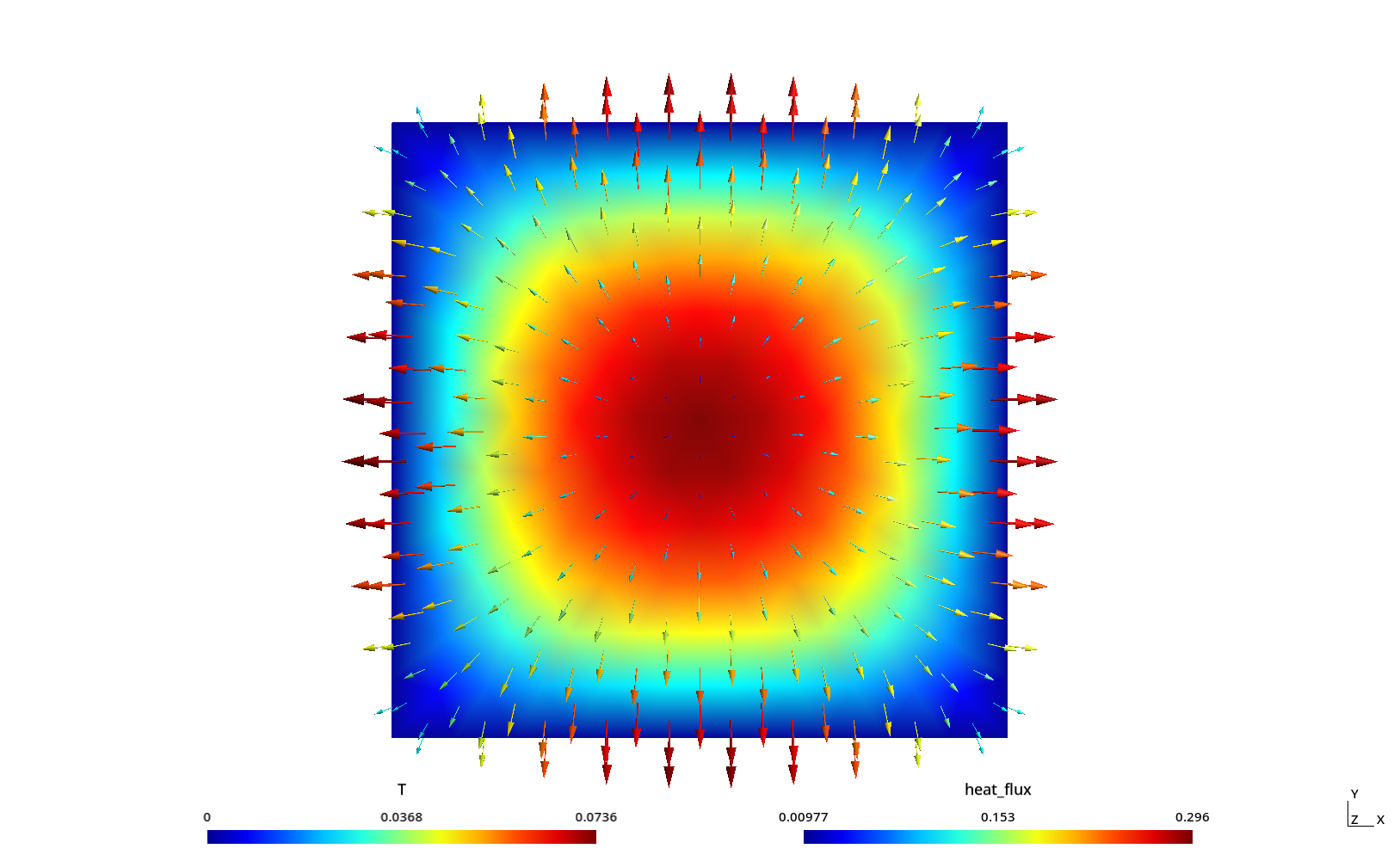
bunny-thermal.feeNote: as we mentioned, the volumetric source
qworks as any other material property. In multi-material problems. it can be defined using variables or functions where the material name is appended to the name or using theMATERIALkeyword.
2.5 Space-dependent properties: manufactured solution
To finish the linear steady-state section, we show how to perform a simple MMS verification using the same unit square as in the previous section.
Make sure you check out the MMS section within the tests directory in the Git repository.
First, let us manufacture a solution temperature, say
T(x,y) = 1 + \sin^2(2x) \cdot \cos^2(3y)
with a certain conductivity
k(x,y) = 1 + x - \frac{y}{2}
which translate to FeenoX ASCII syntax as
T_manufactured(x,y) = 1 + sin(2*x)^2 * cos(3*y)^2
k(x,y) = 1 + x - y/2Then, using the differential equation we can work out what the source
needs to be in order for that manufactured temperature to be the
solution. For that end we use the derivative
functional:1
VAR x' x'' y' y''
q(x,y) = -(derivative(k(x',y) * derivative(T_manufactured(x'',y), x'', x'), x', x) + \
derivative(k(x,y') * derivative(T_manufactured(x,y''), y'', y'), y', y))We also decide that left and top get
Dirichlet conditions:
BC left T=T_manufactured(x,y)
BC top T=T_manufactured(x,y)But bottom and right get Neumann
conditions:
BC bottom q=+(-k(x,y)*derivative(T_manufactured(x,y'),y',y))
BC right q=-(-k(x,y)*derivative(T_manufactured(x',y),x',x))After solving the problem, we want to show that the L_2 error is small. For that end, we use the
INTEGRATE
instruction:
INTEGRATE (T(x,y)-T_manufactured(x,y))^2 RESULT e2Putting everything together:
PROBLEM thermal 2D
READ_MESH square.msh
# manufactured solution
T_manufactured(x,y) = 1 + sin(2*x)^2 * cos(3*y)^2
# conductivity
k(x,y) = 1 + x - y/2
# heat source needed to get the manufactured solution
VAR x' x'' y' y''
q(x,y) = -(derivative(k(x',y) * derivative(T_manufactured(x'',y), x'', x'), x', x) + \
derivative(k(x,y') * derivative(T_manufactured(x,y''), y'', y'), y', y))
# boundary conditions, two fixed temps and two heat fluxes
BC left T=T_manufactured(x,y)
BC top T=T_manufactured(x,y)
BC bottom q=+(-k(x,y)*derivative(T_manufactured(x,y'),y',y))
BC right q=-(-k(x,y)*derivative(T_manufactured(x',y),x',x))
SOLVE_PROBLEM
WRITE_MESH manufactured.vtk T T_manufactured T(x,y)-T_manufactured(x,y)
# compute and show L-2 error
INTEGRATE (T(x,y)-T_manufactured(x,y))^2 RESULT e2
PRINT e2$ feenox manufactured.fee
3.62229e-05
$ Note: once again, make sure you check out the MMS subdirectory in the
testdirectory of the FeenoX repository. A proper verification is performed there by using Maxima to compute the symbolic expressions for the sources and boundary conditions and by sweeping over different mesh sizes (and element types) to show that the convergence rate matches the theoretical value.
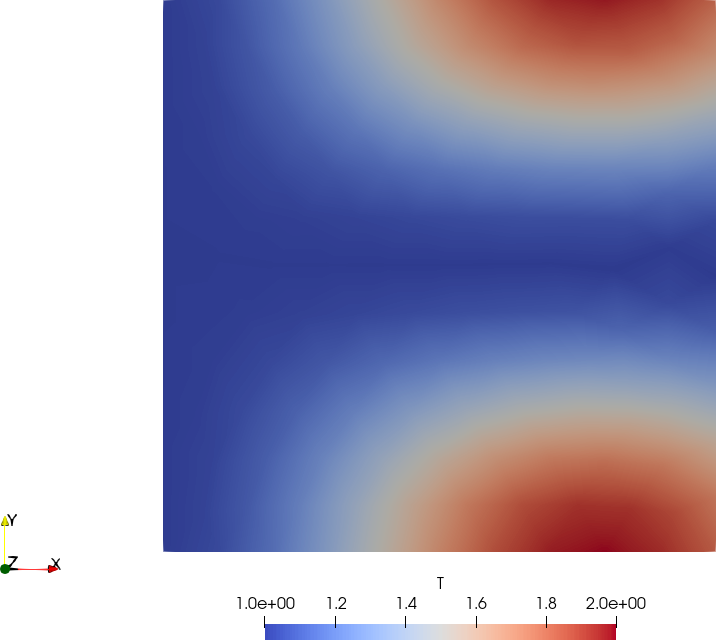
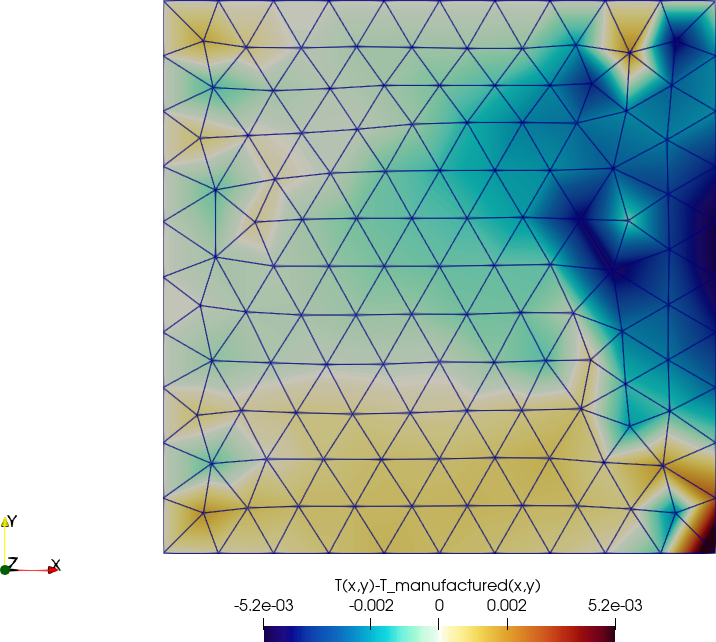
Figure 4: Output of manufactured.fee. a —
Numerical temperature distribution, b — Difference with respect to
manufactured solution
3 Non-linear state-state problems
If in the heat eq. 1 above the thermal conductivity k or the volumetric heat source q depends on the solution T(\mathbf{x}), or the boundary conditions depend non-linearly on T(\mathbf{x}) then the problem is non linear. FeenoX’s parser can detect these dependencies so it will use a non-linear solver automatically. That is to say, there is no need for the user to tell the solver which kind of problem it needs to solve—which is reasonable. Why would the user have to tell the solver?
As we all know, solving a non-linear system of equations is far more complex than solving linear problems. Even more, the most-widely scheme used to solve the non-linear equation \mathbf{F}(\mathbf{u})=0, namely the Newton-Raphson method which is the basis of PETSc’s SNES framework, involves repeatedly solving a linear system starting from an initial guess \mathbf{u}_0:
- Solve J(\mathbf{u}_k) \cdot \Delta \mathbf{u}_k = -\mathbf{F}(\mathbf{u}_k)
- Update \mathbf{u}_{k+1} \leftarrow \mathbf{u}_{k} + \Delta \mathbf{u}_{k}
The matrix J = \mathbf{F}^{\prime}
associated with the linear solve step (which changes from iteration to
iteration) is called the jacobian matrix. FeenoX builds an appropriate
jacobian for each type of non-linearity, ensuring the convergence is as
fast as possible. Advanced users might investigate that indeed J(\mathbf{u}) is correct by using the PETSc
options --snes_test_jacobian and, for smaller problems,
--snes_test_jacobian_view. Note that these options render
the execution far slower, so make sure the mesh is coarse.
The solver options can be changed at runtime either using keywors in
the PROBLEM
definition or command-line options:
NONLINEAR_SOLVER newtonlsor--snes_type=newtonlsLINEAR_SOLVER gmresor--ksp_type=gmresPRECONDITIONER gamgor--pc_type=gamg
Check out the PROBLEM
keyword entry in the FeenoX manual and the links to PETSc’s
documentation for further details. Moreover, advanced users might notice
that some problems might require a non-trivial combination of particular
PETSC options. These can be given in the input file using the PETSC_OPTIONS
definition as well.
3.1 Temperature-dependent heat flux: radiation
One way of introducing a non-linearity is by having a prescribed heat-flux boundary condition to depend on the temperature in a non-linear way. A radiation boundary condition is exactly this, because the heat flux depends on T^4(\mathbf{x}). To illustrate this concept, let us consider the one-dimensional slab x \in [0,1] with uniform conductivity equal to 50 W / (m \cdot K).
- At x=0 (
left) we set a prescribed heat flux equal to 1200 W/m^2. - At x=1 (
right) we set a radiation boundary condition with an emissivity e of 0.8 and an absolute reference temperature of 293.15 K.
This problem, even though it is non-linear, has an analytical solution: a linear interpolation between the temperature at x=1 which is
T(1) = \left( \frac{1200}{\sigma \cdot e} + T_\text{ref}^4\right)^{\frac{1}{4}} and the temperature at x=0
T(0) = T(1) + \frac{1200}{50} where \sigma is the Stefan-Boltzmann constant.
Heads up: just for fun, instead of looking up online its numerical value, we can FeenoX to compute it from the “more fundamental” constants h, c and k_b.
FeenoX uses PETSc’s
SNES framework to solve the resulting non-linear equations. The
available solvers—which can be selected either through
PROBLEM SNES definition or from the command line—are
iterative in nature. The convergence of these algorithms depends on a
good initial guess, which by default is a uniform distribution equal to
the average of all the temperatures T or Tref
that appear on the temperature and convection boundary conditions. Since
in this case we only have heat fluxes, the initial guess would be zero
which might not be appropriate. We can give an explicit initial guess
can be given with the special
function T_guess(x) (or T_guess(x,y) or
T_guess(x,y,z) if the dimensions were two or three).
Putting everything together in a FeenoX input file:
PROBLEM thermal 1D
READ_MESH slab.msh
k = 50 # conductivity (special var)
BC left q=1200 # prescribed heat flux at x=0
# reference temperature for radiation (regular var, used in the expression)
Tref = 293.15
# for fun: compute the Stefan-Boltzmann from fundamental constants
h = 6.62606957e-34 # planck's contant [J s]
c = 299792458 # speed of light in vacuum [m s^(-1)]
k_b = 1.3806488e-23 # boltzmann constant [m^2 kg s^(-2) K^(-1)]
sigma = 2*pi*k_b^4/(h^3*c^2) * integral(1/(t^5*(exp(1/t)-1)), t, 1e-2, infinite)
# sigma = 5.670374419e-8
e = 0.8 # emissivity
# radiation condition at x=1
BC right q=sigma*e*(Tref^4-T(x)^4)
T_guess(x) = Tref # initial guess
SOLVE_PROBLEM
PRINT T(0) (1200/(sigma*e)+Tref^4)^(1/4)+1200/50
PRINT T(1) (1200/(sigma*e)+Tref^4)^(1/4)We can run FeenoX with the PETSc option --snes_monitor
to check how the residuals converge as the iterative non-linear solver
proceeds:
$ feenox radiation-as-heatflux-kelvin.fee --snes_monitor
0 SNES Function norm 1.200000000000e+03
1 SNES Function norm 1.013534450309e+03
2 SNES Function norm 8.205392002604e+02
3 SNES Function norm 1.010983873807e+02
4 SNES Function norm 2.318614629013e+00
5 SNES Function norm 1.311027509018e-03
6 SNES Function norm 3.975272228975e-10
452.897 452.897
428.897 428.897
$In this case we used SI units with absolute temperatures. If we wanted to get the temperature in Celsius, we could have done:
PROBLEM thermal 1D
READ_MESH slab.msh
k = 50
BC left q=1200
BC right q=5.670374419e-8*0.8*((20+273.15)^4-(T(x)+273.15)^4)
T_guess(x) = 20
SOLVE_PROBLEM
PRINT T(0)
PRINT T(1)Homework
- Rewrite the radiation boundary condition as a convection condition. Hint: note that T^4 - T_\text{ref}^4 is a difference of squares. Look for
radiation-as-convection.feein FeenoX’stestsdirectory for the answer.- Explain why the solver converges even though there are no prescribed temperature conditions. Hint: think of it as a convection condition.
3.2 Temperature-dependent conductivity
Another general source of non-linearity in engineering problems modeled as PDEs is due to material properties depending on the unknown. For steady-state heat conduction, this happens when the thermal conductivity depends on the temperature as a certain function k(T). In general, this dependency is given either using
- an algebraic expression with a correlation of experimental data, or
- a pointwise-defined “table” with the actual experimental data
FeenoX can understand both of them. In this section we use the former, and in the next section we use the latter. Consider a pellet of uranium dioxide as the ones used inside the fuel elements of nuclear power reactors. According to “Thermophysical Properties of Materials For Nuclear Engineering”, the thermal conductivity of UO_2 can be approximated by
k(\tau) [ \text{W} \cdot \text{m}^{-1} \cdot \text{K}^{-1} ] = \frac{100}{7.5408 + 17.692 \cdot \tau + 3.614 \tau^2} + \frac{6400}{t^{5/2}} \cdot \exp \left( \frac{-16.35}{\tau} \right) where \tau = T [ \text{K} ] / 1000.
How do we tell FeenoX to use this correlation? Easy: we define a
special function of space like k(x,y,z) that uses to this
correlation with T(x,y,z) as the argument. If we want
T in Kelvin:
VAR T'
tau(T') = T'/1000
cond(T') = 100/(7.5408 + 17.692*tau(T') + 3.614*tau(T')^2) + 6400/(tau(T')^(5/2))*exp(-16.35/tau(T'))
# k is in W/(m K)
k(x,y,z) = cond(T(x,y,z))If we want T in Celsius:
# T is in Celsius, T' is in Kelvin
VAR T'
tau(T') = (T'+273.15)/1000
cond(T') = 100/(7.5408 + 17.692*tau(T') + 3.614*tau(T')^2) + 6400/(tau(T')^(5/2))*exp(-16.35/tau(T'))
# k is in W/(m K)
k(x,y,z) = cond(T(x,y,z))Two points to take into account:
The symbol
Tis already reserved for the solution field, which is a function of spaceT(x,y,z), at the time thePROBLEMkeyword is parsed. Therefore, we cannot useTas a variable. If we definedtau(T), we would get$ feenox pellet-non-linear-k-uniform-q.fee error: pellet-non-linear-k-uniform-q.fee: 4: there already exists a function named 'T' $If we tried to define
tau(T)beforePROBLEM, then FeenoX would fail when trying to allocate space for thethermalproblem solution as there would already be defined a symbolTfor the argument oftau.When giving a non-uniform conductivity as a special function, this function has to be a function of space
k(x,y,z). The dependence on temperature is introduced by using the solutionTevaluated at point(x,y,z). That is why we defined the correlation as a function of a single variable and then defined the conductivity as the correlation evaluated atT(x,y,z). But if we used theMATERIALSkeyword, we could have directly written the whole expression:MATERIAL uo2 "k=100/(7.5408 + 17.692*tau(T(x,y,z)) + 3.614*tau(T(x,y,z))^2) + 6400/(tau(T(x,y,z))^(5/2))*exp(-16.35/tau(T(x,y,z)))"Note: since the expression is fairly long and complex, we used spaces to separate terms. But the
MATERIALkeyword expectsk=...to be a single token. Hence, we quoted the whole thing as"k=1 + ...".
Other than this, we are ready to solve for the temperature distribution in a UO_2 pellet with a uniform power source (we will refine the power source and make it more interesting later on). The geometry is half a fuel pellet with
- symmetry conditions on the base (
symmetryin the mesh) - prescribed temperature on the external surface
(
externalin the mesh) - convection on the top surface (
gapin the mesh) - a uniform power source
All the values for these conditions are uniform and correspond roughly to actual figures found in a power nuclear reactor core.
PROBLEM thermal
READ_MESH pellet.msh SCALE 1e-3 # mesh is in mm, we want it in meters so we scale it
# T is in Celsius, T' is in Kelvin
VAR T'
tau(T') = (T'+273.15)/1000
cond(T') = 100/(7.5408 + 17.692*tau(T') + 3.614*tau(T')^2) + 6400/(tau(T')^(5/2))*exp(-16.35/tau(T'))
# k is in W/(m K)
k(x,y,z) = cond(T(x,y,z))
# q is in W / m^3 = 300 W/cm * 100 cm/m / area
q = 300 * 100 / (pi*(4e-3)^2)
BC symmetry q=0
BC external T=420
BC gap h=100 Tref=400
T_guess(x,y,z) = 800
SOLVE_PROBLEM
PRINT T_max
WRITE_RESULTS # default is .msh formatThe execution with --snes_monitor should give something
like this:
$ feenox pellet-non-linear-k-uniform-q.fee --snes_monitor
0 SNES Function norm 8.445939693892e+03
1 SNES Function norm 2.730091094770e+00
2 SNES Function norm 4.316892050932e-02
3 SNES Function norm 1.021064388940e-05
1094.77
$ 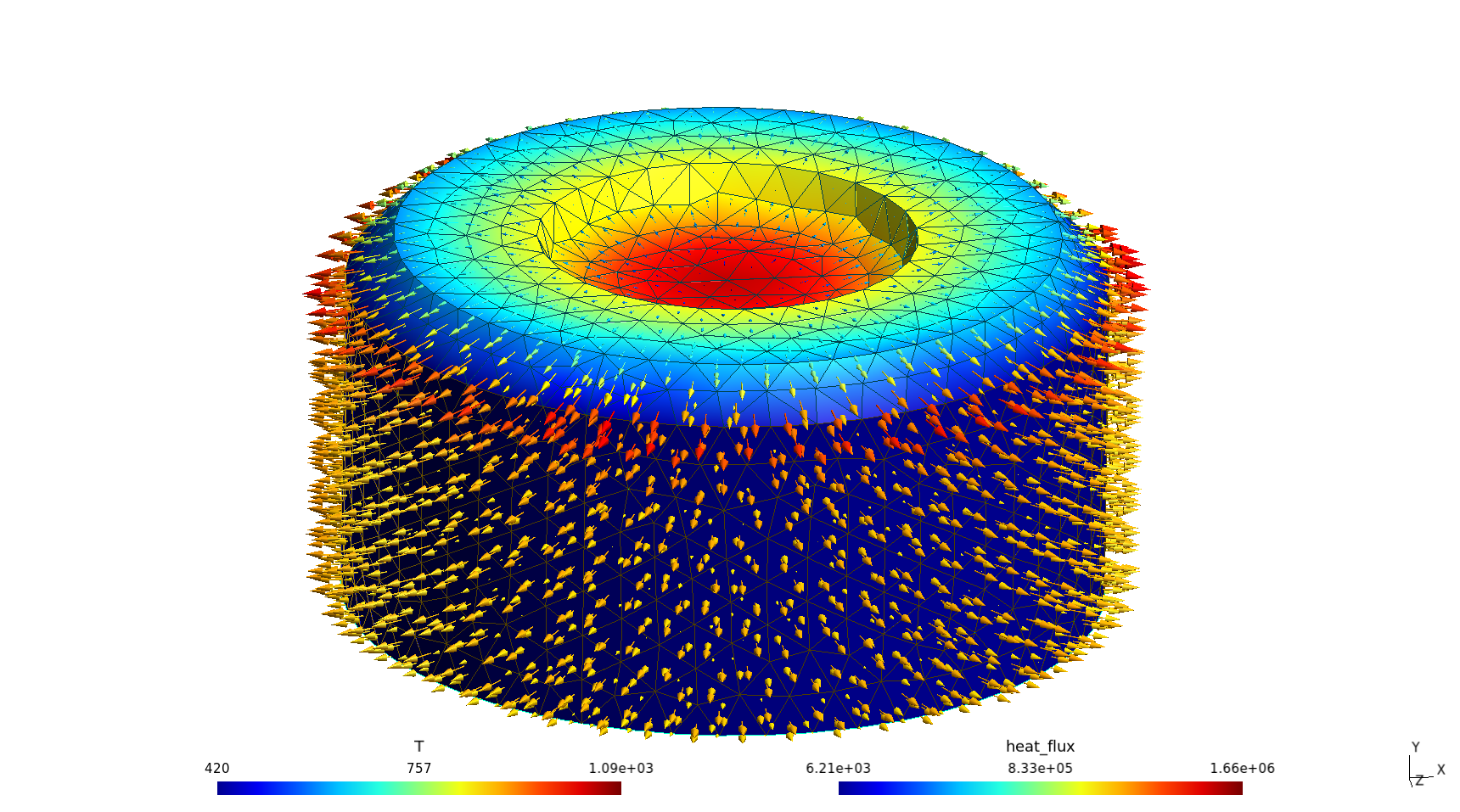
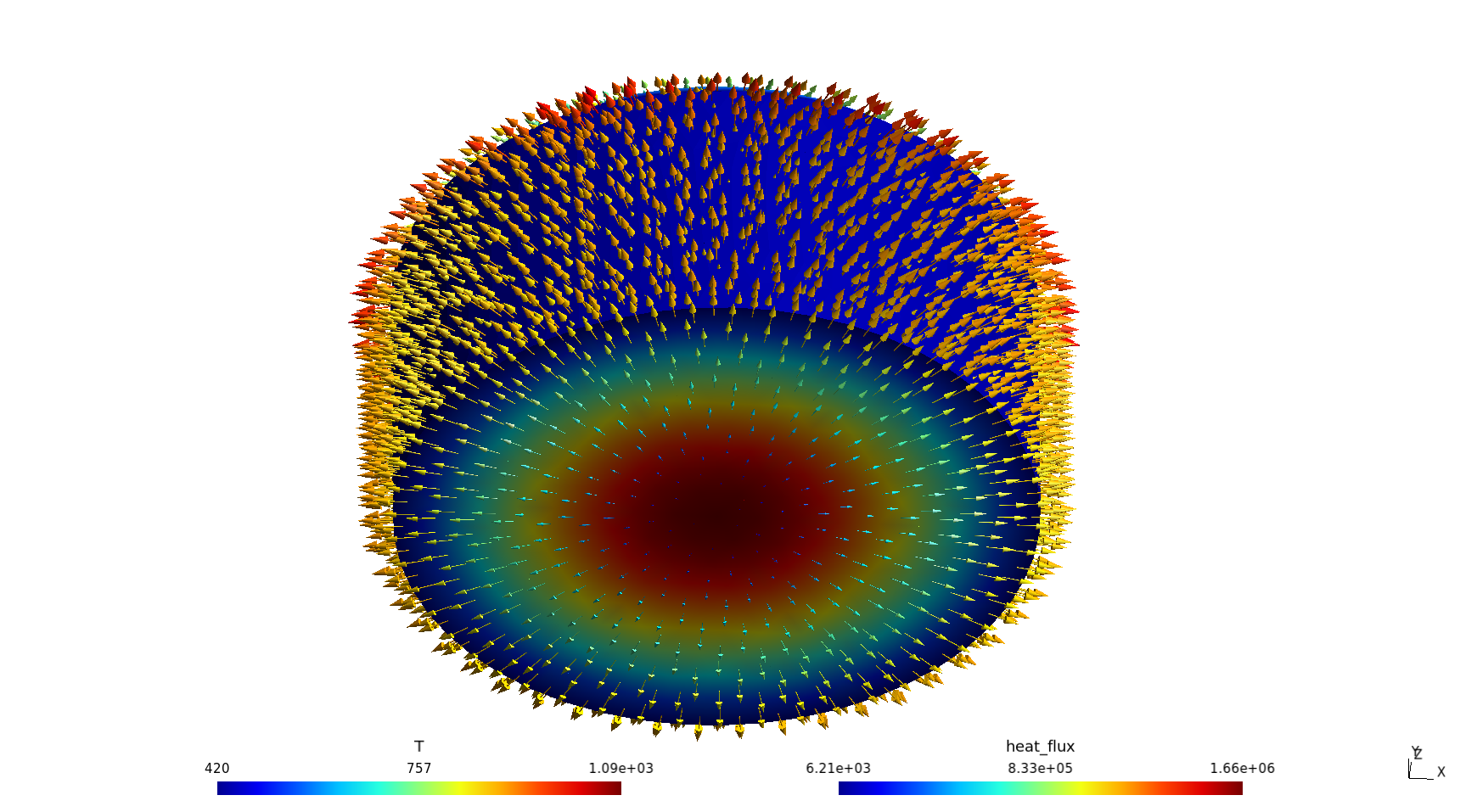
Figure 5: Temperature and heat flux distribution for a half UO_2 pellet with uniform power source.. a — Top view, b — Bottom view (symmetry)
If we comment out the line with the initial guess, then FeenoX does converge but it needs one step more:
$ feenox pellet-non-linear-k-uniform-q.fee --snes_monitor
0 SNES Function norm 2.222870199708e+02
1 SNES Function norm 6.228090579878e-01
2 SNES Function norm 4.109509310386e-02
3 SNES Function norm 1.603956028971e-04
4 SNES Function norm 2.124156299986e-09
1094.77
$ If, for some reason, we do not want to solve this problem as non-linear, then we can force FeenoX to solve it as if it was a linear problem. We can either choose so from the input file writing
PROBLEM thermal LINEARor by passing --linear in the command-line options:
$ feenox pellet-non-linear-k-uniform-q.fee --snes_monitor --linear
717.484
WARNING! There are options you set that were not used!
WARNING! could be spelling mistake, etc!
There is one unused database option. It is:
Option left: name:-snes_monitor (no value) source: command line
$ 3.3 Temperature-dependent sources
The volumetric power generated by fissioning nuclei of ^{235}U in the UO_2 is not uniform throughout the fuel. It depends on…
- The location of the fuel bundle inside the core: in general, pellets located near the center dissipate more power than those located at the periphery).
- The location of the pellet inside the fuel element: the effect depends on the reactor design but for reactors where the moderator is separated from the coolant, this change is very significative.
- The spatial location \mathbf{x} inside the pellet: points near the periphery of the pellet now dissipate more power than those located in the bulk because they “have access” to more moderated neutrons coming from the outside.
- The temperature T(\mathbf{x}): hot nuclei are less likely to fission.
along with other nuclear-related stuff such as fuel burn-up, concentration of poisons, control systems, etc.
Anyway, this is a tutorial about FeenoX capabilities. Our goal here is to show what FeenoX can do and how to ask it to to such things. So let us model a custom power source depending both on space and on the local temperature like
q(x,y,z) = q_0 \cdot (1 + 20~\text{mm}^{-1} \cdot x) \cdot \left[1 - \frac{ T(x,y,z)-800~\text{ºC}}{2000 ~\text{ºC}} \right]
Note: According to Le Chatelier’s principle, the power should decrease when the temperature increases.
To also illustrate how to set a conductivity that depends directly on
interpolated experimental data, in this case we use the numerical data
from the IAEA report above by defining cond(T') as a
function of type DATA:
VAR T'
FUNCTION cond(T') INTERPOLATION steffen DATA {
400 4.74
450 4.50
500 4.28
550 4.07
600 3.89
650 3.91
700 3.55
750 3.40
800 3.26
850 3.13
900 3.01
950 2.90
1000 2.79
1050 2.70
1100 2.61
1132 2.55
1150 2.52
1200 2.45 }Since we want to compare the temperature distribution using this
non-linear power source with respect to the previous case with uniform
power, we read back the temperature we wrote with the instruction WRITE_RESULTS.
With no further arguments, that instruction writes a .msh
file with the temperature distribution T as a scalar field
and the three heat fluxes qx, qy and
qz as a vector—which we used to create fig. 5. If no
FILE keyword is given, the default mesh file is named like
the FeenoX input file with the extension .fee renamed to
.msh. So we can then ask FeenoX to retrieve the old
temperature distribution as a function of space, with a new name (since
there is already a function T), say
T_uniform:
READ_MESH pellet-non-linear-k-uniform-q.msh DIM 3 READ_FIELD T as T_uniformNow we can write the results, including the algebraic difference (or
any other operation) of T and T_uniform. For
that end, we now use WRITE_MESH
and enter the expression we want to write into the output mesh:
WRITE_MESH $0.vtk T T(x,y,z)-T_uniform(x,y,z) q VECTOR qx qy qz Note: If the input file does not explicitly ask for the heat fluxes or does not have the instruction
WRITE_RESULTS, then the heat fluxes are not computed at all to save CPU time.
To illustrate that things do not need to be only one way (i.e. Unix
rule of diversity), we now write a VTK post-processing file (instead
of .msh like in the previous case). Since
WRITE_MESH is a generic instruction (while
WRITE_RESULTS is PDE-aware so it knows which are the
available fields) we have to list what we want to write in the VTK:
- The current temperature distribution
T. SinceTis a function of space, there is no need to pass the arguments(x,y,z), it will be understood as “write the function of spaceTin the output mesh.” - The algebraic difference between the current temperature distribution and the one read from last case’s output. This time, we are asking FeenoX to write an algebraic expression, so the arguments of both functions are needed.
- The heat power source
qas a scalar function of space. Again, no need to give the arguments. - A three-dimensional vector whose three components are the three heat fluxes.
By default, WRITE_MESH writes nodal-based fields. If the
CELLS keyword is used, all the following fields are written
as cell-based fields, until the NODES keyword appears again
(or until there are no more fields, of course).
Note: In this case the “old” mesh is the very same as the “current” mesh. Therefore, no interpolation is needed and the difference T(x,y,z)-T_\text{uniform}(x,y,z) will be evaluated node by node. But if the mesh over which T_\text{uniform}(x,y,z) was different (even with a different element order), then FeenoX would be able to interpolate it at the nodes (or cell centers) of the new mesh. See https://github.com/gtheler/feenox-non-conformal-mesh-interpolation.
Putting everything together, we have:
PROBLEM thermal
READ_MESH pellet.msh SCALE 1e-3 # mesh is in mm, we want it in meters so we scale it
VAR T'
FUNCTION cond(T') INTERPOLATION steffen DATA {
400 4.74
450 4.50
500 4.28
550 4.07
600 3.89
650 3.91
700 3.55
750 3.40
800 3.26
850 3.13
900 3.01
950 2.90
1000 2.79
1050 2.70
1100 2.61
1132 2.55
1150 2.52
1200 2.45 }
k(x,y,z) = cond(T(x,y,z))
# q is in W / m^3 = 300 W/cm * 100 cm/m / area
q0 = 300 * 100 / (pi*(4e-3)^2)
q(x,y,z) = q0 * (1+60*x) * (1-(T(x,y,z)-800)/800)
BC symmetry q=0
BC external T=420
BC gap h=100 Tref=400
T_guess(x,y,z) = 800
SOLVE_PROBLEM
PRINT T_max
READ_MESH pellet-non-linear-k-uniform-q.msh DIM 3 READ_FIELD T as T_uniform
WRITE_MESH $0.vtk T T(x,y,z)-T_uniform(x,y,z) q VECTOR qx qy qz which we can run as simply as
$ feenox pellet-non-linear-k-non-linear-q.fee
1026.17
$ to get an output VTK file we can then further post-process to get fig. 6.


Figure 6: Results for the non-uniform power case. a — Temperature difference with respect to the uniform power case, b — Volumetric power source distribution
4 Transient problems
In this final section of the tutorial we solve the transient heat conduction equation
\rho(\mathbf{x}, T,t) \cdot c_p(\mathbf{x}, T,t) \cdot \frac{\partial T}{\partial t} - \text{div} \Big[ k(\mathbf{x}, T,t) \cdot \text{grad} \left[ T(\mathbf{x},t)\right] \Big] = q(\mathbf{x}, T,t)
For this end, we need the product of the density \rho and heat capacity c_p. This product can be given by either
rhoandcpseparatelyrhocpas a single property- the thermal diffusivity
kappa(equal to k / (\rho \cdot c_p))
As with any other transient problem in FeenoX, it is triggered by
setting the special
variable end_time to a positive value. FeenoX uses PETSc’s TS framework for
transient problems. By default, it uses an adaptive time stepper. An
initial \Delta t can be given with the
special variable dt.
The range can be controlled with min_dt
and max_dt,
which can be expressions of the special variable t.
If one needs to stop the transient problem before it reaches the
prescribed end_time, the special variable done
can be set to true. After the next PROBLEM_SOLVE
instruction, the transient problem will finish.
The initial condition can be given by defining a function
T_0 of space. If there is no T_0 defined, the
initial condition is obtained by solving a steady-state problem
with t=0.
4.1 From an initial condition up to steady state
One common way of solving a time-dependent problem is to start with a certain initial temperature distribution (say everything is uniformly “cold”) and then “do nothing” and wait until the steady-state conditions are achieved. In effect, let us consider again the unitary one-dimensional slab with
- a uniform thermal conductivity k=1
- a uniform thermal diffusivity \kappa=1
- a uniformly distributed power source q=1
subject to T=0 at both ends. From heat conduction theory, we know the steady state temperature will be a parabola that goes from zero at x=0 to a maximum value q/(8k) at x=1/2 and then back to zero at T=0. Let us solve this transient case with FeenoX:
PROBLEM thermal 1d
READ_MESH slab.msh
# if end_time > 0 then we are in a transient problem
end_time = 2
# we can hint the solver what the first dt has to be
dt_0 = 1e-3
# if there exists a function of space T_0 then that's the initial condition
T_0(x) = 0
k = 1
q = 1
kappa = 1
BC left T=0
BC right T=0
SOLVE_PROBLEM
# now t is a variable that holds the time
# and dt holds the (variable) time step
PRINT %.4f t dt %.6f T(1/2)$ feenox slab-uniform-transient-from-zero.fee
0.0000 0.0010 0.000000
0.0010 0.0017 0.001000
0.0027 0.0033 0.002663
0.0059 0.0033 0.005914
0.0092 0.0039 0.009195
0.0131 0.0051 0.013068
0.0182 0.0067 0.018146
0.0249 0.0084 0.024665
0.0333 0.0103 0.032534
0.0436 0.0127 0.041471
0.0563 0.0158 0.051386
0.0721 0.0189 0.062179
0.0910 0.0206 0.073040
0.1116 0.0217 0.082798
0.1333 0.0230 0.091131
0.1563 0.0245 0.098173
0.1808 0.0263 0.104087
0.2071 0.0285 0.109013
0.2356 0.0311 0.113064
0.2667 0.0341 0.116340
0.3008 0.0378 0.118929
0.3386 0.0422 0.120922
0.3808 0.0477 0.122405
0.4285 0.0546 0.123462
0.4831 0.0636 0.124176
0.5468 0.0757 0.124622
0.6225 0.0927 0.124872
0.7152 0.1178 0.124988
0.8330 0.1576 0.125023
0.9906 0.2280 0.125020
1.2186 0.3764 0.125008
1.5950 0.4050 0.125000
2.0000 0.8101 0.124999
$ Note that:
- The special variable
end_timecontrols the final time. - The special variable
dtholds the actual time step. It is not a good idea to set the actual value ofdtbecause it gets overwritten by the time stepper. But you can setmin_dtandmax_dt, which in turn can be expressions of the timet. If you setmin_dtandmax_dtto the same value, the time step will be uniform (although internally FeenoX might take internal sub-steps to take into account the errors in the derivatives) - If there exists a function of space named
T_0then that will be the initial condition. If not, a steady-state problem is solved (with all the expressions evaluated witht=0) and that solution is the initial condition. - All the variable assignments and expressions in material properties
which depend on the time
tare re-evaluated at each time step, and possibly at other times as the time stepper considers fit to see if it can increase (or if it has to decrease) the time stepdt. - The transient solver and the time-adaptation schemes can be chosen
with the keywords
TRANSIENT_SOLVERandTIME_ADAPTATIONin thePROBLEMkeyword or with the--ts_typeand--ts_adapt_typecommand-line options. - All the instructions, including
PRINTandWRITE_RESULTSare executed in each time step.
There might be cases where the end time is not known beforehand and
we might want to stop the computation once a certain condition is met.
For this end, FeenoX has the special variable done which
can be set to a non-zero value to indicate the computation has to stop.
For instance, instead of going up to t=2 we can ask FeenoX to stop once the
temperature at the center is within 1% of the theoretical steady-state
value:
PROBLEM thermal 1d
READ_MESH slab.msh
end_time = 2
dt_0 = 1e-3
T_0(x) = 0
k = 1
q = 1
kappa = 1
BC left T=0
BC right T=0
SOLVE_PROBLEM
done = abs((T(1/2)-q/(8*k))/(q/(8*k))) < 1e-2
PRINT %.4f t dt %.6f T(1/2)$ feenox slab-uniform-transient-from-zero-done.fee
0.0000 0.0010 0.000000
0.0010 0.0017 0.001000
0.0027 0.0033 0.002663
0.0059 0.0033 0.005914
0.0092 0.0039 0.009195
0.0131 0.0051 0.013068
0.0182 0.0067 0.018146
0.0249 0.0084 0.024665
0.0333 0.0103 0.032534
0.0436 0.0127 0.041471
0.0563 0.0158 0.051386
0.0721 0.0189 0.062179
0.0910 0.0206 0.073040
0.1116 0.0217 0.082798
0.1333 0.0230 0.091131
0.1563 0.0245 0.098173
0.1808 0.0263 0.104087
0.2071 0.0285 0.109013
0.2356 0.0311 0.113064
0.2667 0.0341 0.116340
0.3008 0.0378 0.118929
0.3386 0.0422 0.120922
0.3808 0.0477 0.122405
0.4285 0.0546 0.123462
0.4831 0.0636 0.124176
$ If the initial condition does not satisfy the Dirichlet boundary conditions, the solver might struggle to converge for small times. One way of overcoming this issue is to go the other way round: make sure the boundary conditions match the initial condition at the boundaries for t=0 and then “quickly” move the boundary condition to the actual value. For example, if the condition was T(1)=1 instead of T(1)=0 and we blindy wrote
PROBLEM thermal 1d
READ_MESH slab.msh
end_time = 2
dt_0 = 1e-3
T_0(x) = 0
k = 1
q = 1
kappa = 1
BC left T=0
BC right T=1
SOLVE_PROBLEM
PRINT %.4f t dt %.6f T(1/2)we would get
$ feenox slab-uniform-transient-from-zero-one-naive.fee
0.0000 0.0010 0.000000
[0]PETSC ERROR: --------------------- Error Message --------------------------------------------------------------
[0]PETSC ERROR: TSStep has failed due to DIVERGED_STEP_REJECTED
[0]PETSC ERROR: See https://petsc.org/release/faq/ for trouble shooting.
[0]PETSC ERROR: Petsc Release Version 3.20.0, Sep 28, 2023
[0]PETSC ERROR: feenox on a double-int32-release named tom by gtheler Sat Dec 9 11:23:52 2023
[0]PETSC ERROR: Configure options --download-eigen --download-hdf5 --download-hypre --download-metis --download-mumps --download-parmetis --download-scalapack --download-slepc --with-64-bit-indices=no --with-debugging=no --with-precision=double --with-scalar-type=real COPTFLAGS=-O3 CXXOPTFLAGS=-O3 FOPTFLAGS=-O3
[0]PETSC ERROR: #1 TSStep() at /home/gtheler/libs/petsc-3.20.0/src/ts/interface/ts.c:3398
[0]PETSC ERROR: #2 TSSolve() at /home/gtheler/libs/petsc-3.20.0/src/ts/interface/ts.c:4015
[0]PETSC ERROR: #3 feenox_problem_solve_petsc_transient() at pdes/petsc_ts.c:83
error: PETSc error
$ But if we do this instead
PROBLEM thermal 1d
READ_MESH slab.msh
end_time = 2
dt_0 = 1e-3
T_0(x) = 0
k = 1
q = 1
kappa = 1
BC left T=0
BC right T=limit(1e6*t,0,1)
SOLVE_PROBLEM
PRINT %.4f t dt %.6f T(1/2)we get the right answer, paying some inital cost as small time steps:
$ feenox slab-uniform-transient-from-zero-one-smart.fee
0.0000 0.0010 0.000000
0.0000 0.0000 0.000002
0.0000 0.0000 0.000002
0.0000 0.0000 0.000002
0.0000 0.0000 0.000002
0.0000 0.0000 0.000002
0.0000 0.0000 0.000002
0.0000 0.0000 0.000002
0.0000 0.0000 0.000003
0.0000 0.0000 0.000005
0.0000 0.0000 0.000008
0.0000 0.0000 0.000014
0.0000 0.0000 0.000026
0.0000 0.0000 0.000049
0.0001 0.0001 0.000094
0.0001 0.0001 0.000177
[...]
0.9534 0.1495 0.625030
1.1030 0.2130 0.625031
1.3160 0.3419 0.625014
1.6578 0.3422 0.625001
2.0000 0.6843 0.624999
$ 4.2 From a steady state
Another usual requirement is to start from a steady state, disturb the system and see how this disturbance proceeds over time. Disturbances may come from
- time-dependent boundary conditions
- time-dependent material properties, or
- time-dependent power sources.
Let us consider the following industrial-grade problem, taken from https://github.com/seamplex/piping-asme-fatigue. A valve in a certain system within a power plant (fig. 7 (a)) is made out of stainless steel (green), but it is connected through the output nozzle to a carbon steel pipe (magenta). Since the geometry (and the boundary conditions) are symmetric, we can differentiate three external surfaces (fig. 7 (b))
- Symmetry plane (yellow)
- Internal surface (cyan)
- External surface (pink)
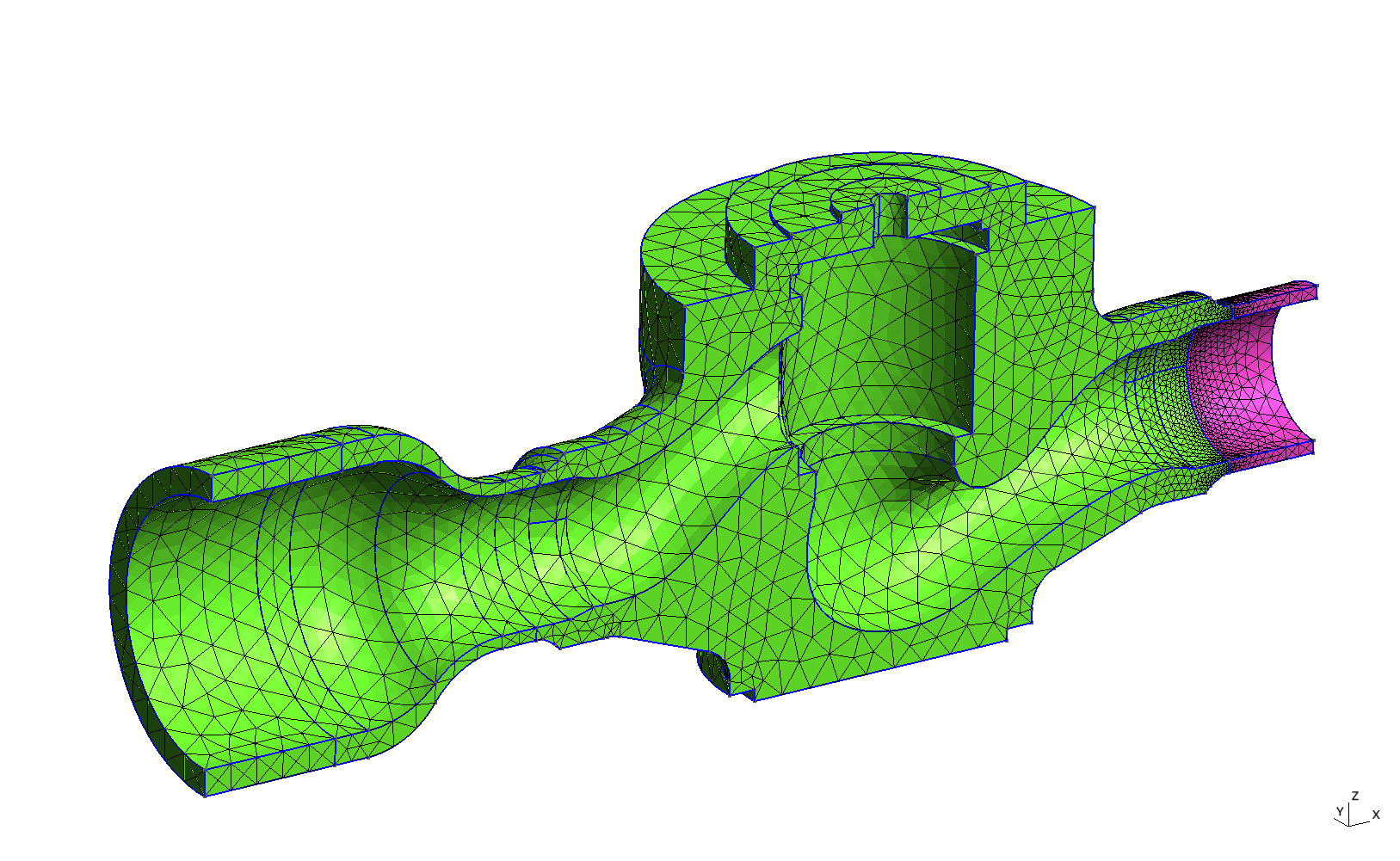
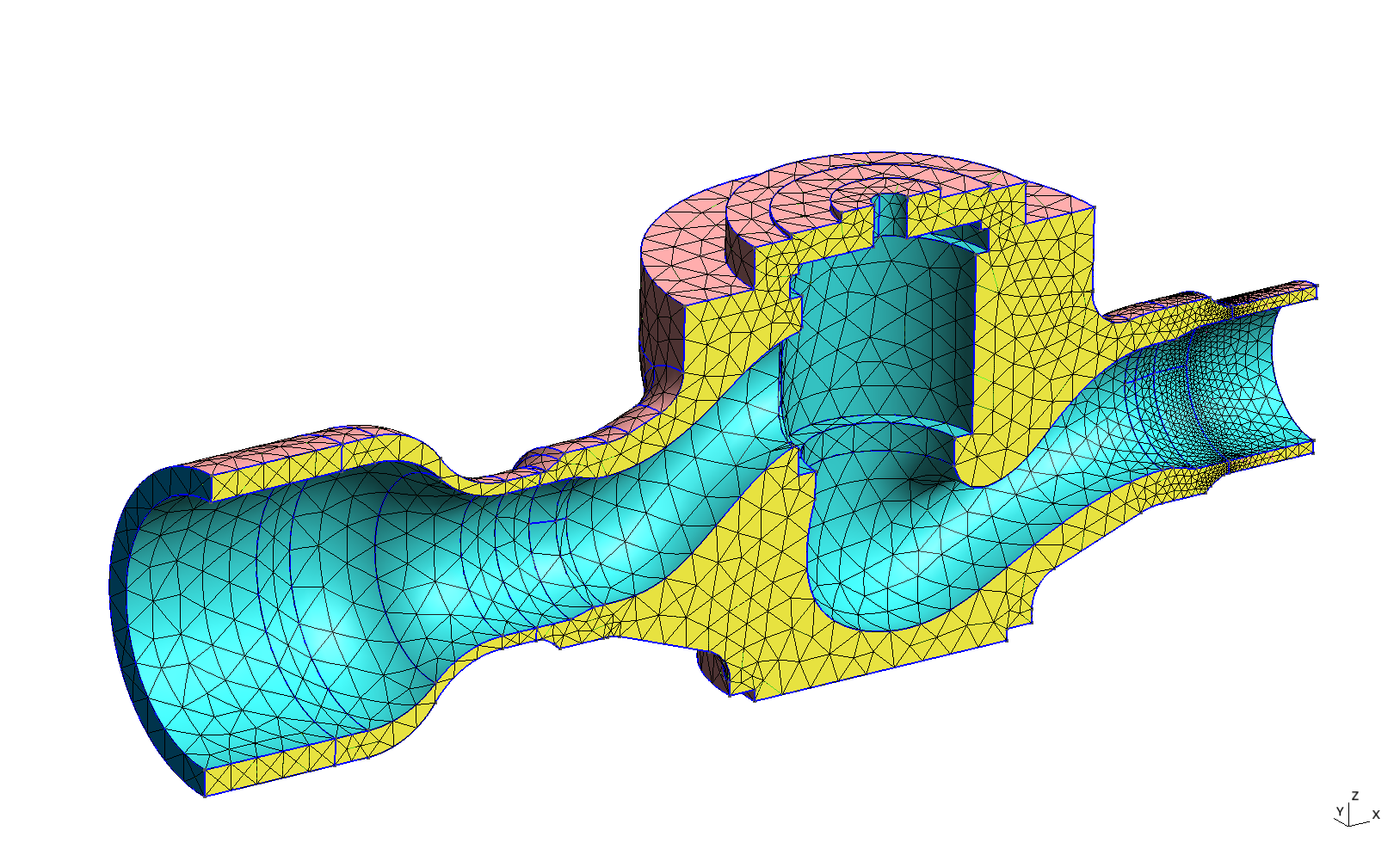
Figure 7: Physical groups for the valve problem. a — Volumetric labels, b — Surface labels
The Gmsh’s .geo file to mesh a continuous CAD in BREP
format and define such physical groups is:
SetFactory("OpenCASCADE");
// read the BREP
Merge "valve.brep";
// meshing settings
Mesh.ElementOrder = 1;
Mesh.Optimize = 1;
Mesh.OptimizeNetgen = 1;
Mesh.Algorithm = 6; // (1=MeshAdapt, 2=Automatic, 5=Delaunay, 6=Frontal, 7=BAMG, 8=DelQuad)
Mesh.Algorithm3D = 10; // (1=Delaunay, 2=New Delaunay, 4=Frontal, 5=Frontal Delaunay, 6=Frontal Hex, 7=MMG3D, 9=R-tree)
Mesh.CharacteristicLengthMax = 24;
Mesh.CharacteristicLengthMin = 0.1*Mesh.CharacteristicLengthMax;
// local refinement
Field[1] = Distance;
Field[1].FacesList = {16};
Field[2] = Threshold;
Field[2].IField = 1;
Field[2].LcMin = Mesh.CharacteristicLengthMin;
Field[2].LcMax = Mesh.CharacteristicLengthMax;
Field[2].DistMin = 5;
Field[2].DistMax = 130;
Background Field = 2;
// carbon steel
Physical Volume("CS", 1) = {2};
// stainless stell
Physical Volume("SS", 2) = {1,3,4};
// bcs
Physical Surface("symmetry", 3) = {3, 4, 15, 17, 20, 25, 91, 110, 111};
Physical Surface("internal", 4) = {7, 8, 9, 10, 18, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 60, 61, 62, 63, 64, 65, 66, 67, 68, 97, 98, 99, 100, 101, 112};
Physical Surface("external", 5) = {1, 2, 6, 12, 13, 19, 21, 22, 23, 24, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 54, 55, 56, 57, 58, 59, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 92, 93, 94, 95, 96, 102, 103, 104, 105, 106, 107, 108};
// these are needed to compute the mean value
Physical Surface("end_carbon", 6) = {14};
Physical Surface("end_ss", 7) = {109};The transient problem we are going to solve is to find out the temperature distribution that results from a relatively simple operational transient by changing the internal temperature of the pipe in a certain prescribed way as a function of time. Since we want to be flexible (as in the original example at https://github.com/seamplex/piping-asme-fatigue) we are going to ask FeenoX to read the prescribed internal temperature vs. time from a text file containing the (t,T(t)) pairs. Moreover, we are going to assume there are many files with many transients and we want to pick which one to choose from the command line.
We do this by using the $1 wildcard: it will be expanded
to the first argument in the command line after the input file. If none
is provided, then FeenoX will complain unless we provide a default value
with the definition DEFAULT_ARGUMENT_VALUE:
DEFAULT_ARGUMENT_VALUE 1 1
FUNCTION Tint(t) FILE valve-internal-$1.csv INTERPOLATION linearThese lines mean “define a function Tint(t) by
linearly-interpolating the data in the file
valve-internal-$1.csv where $1 is the argument
after the input file in the command line or 1 if none is
provided. See the documentation for the FUNCTION
definition for other available interpolation schemes.
The CSV file should contain something like
$ cat valve-internal-1.csv
0 40
100 250
500 250
600 40
1000 40
$ We want the final time to be equal to the last time defined in the
transient, which we do not know at the time we are preparing the input
file. But FeenoX provides the definition (and data) points for all the
point-wise functions as VECTORs,
which we can then use to define end_time as the vecmax
of vec_Tint_t:
end_time = vecmax(vec_Tint_t)Boundary conditions are
- Prescribed temperature equal to T_\text{int}(t) at
internal(cyan) - Convection with a fixed reference temperature equal to 50ºC at
external(pink) - Zero heat flux (adiabatic condition) at
symmetry(yellow)
which easily translate to
BC internal T=Tref(t)
BC external h=1e-6 Tref=50
BC symmetry q=0The temperature-dependent material properties come from the tables in
ASME code div II section D. Check out the included file asme-properties.fee
for details:
INCLUDE asme-properties.fee
MATERIAL CS k=k_carbon(T(x,y,z))*1e-3 kappa=kappa_carbon(T(x,y,z))
MATERIAL SS k=k_312(T(x,y,z))*1e-3 kappa=kappa_312(T(x,y,z))The full input file is then
PROBLEM thermal 3D
READ_MESH valve.msh
DEFAULT_ARGUMENT_VALUE 1 1 # no extra args means $1=1
# read the internal pipe temperature vs. time
FUNCTION Tint(t) FILE valve-internal-$1.csv INTERPOLATION linear
# the vector vec_Tint_t has all the times in the file
# so vecmax() gives the last definiton time
end_time = vecmax(vec_Tint_t)
BC internal T=Tint(t)
BC external h=1e-6 Tref=50
BC symmetry q=0
INCLUDE asme-properties.fee
MATERIAL CS k=k_carbon(T(x,y,z))*1e-3 kappa=kappa_carbon(T(x,y,z))
MATERIAL SS k=k_312(T(x,y,z))*1e-3 kappa=kappa_312(T(x,y,z))
SOLVE_PROBLEM
INCLUDE valve-scl-coords.fee
# output temperatures at the SCL to stdout
PRINT %g t %.3f Tint(t) {
T(scl_xi(2),scl_yi(2),scl_zi(2))
T(0.5*(scl_xi(2)+scl_xf(2)),0.5*(scl_yi(2)+scl_yf(2)),0.5*(scl_zi(2)+scl_zf(2)))
T(scl_xf(2),scl_yf(2),scl_zf(2))
T(scl_xi(4),scl_yi(4),scl_zi(4))
T(0.5*(scl_xi(4)+scl_xf(4)),0.5*(scl_yi(4)+scl_yf(4)),0.5*(scl_zi(4)+scl_zf(4)))
T(scl_xf(4),scl_yf(4),scl_zf(4))
}
# write detailed distributions to a Gmsh file (including the $1 value)
WRITE_RESULTSThe idea is to run the input file through FeenoX and pipe (in the Unix sense, not
in the mechanical sense) the standard output to an ASCII file which we
can plot to monitor temperatures at certain locations (around ASME’s
stress classification lines, for example as in fig. 8). The detailed
results are written into a file valve-1.msh (or whatever
$1 expands to) which can then be used to create an
animation of the temperature T(\vec{x},t) and the heat flux \vec{q}(\vec{x},t):
$ feenox valve.fee 1 | tee valve-1.csv
0 40.000 40.000 40.004 40.008 40.000 40.004 40.007
0.0625 40.131 40.131 40.004 40.008 40.131 40.004 40.007
0.143101 40.301 40.301 40.005 40.008 40.301 40.004 40.007
0.272711 40.573 40.573 40.018 40.008 40.573 40.005 40.007
0.430269 40.904 40.904 40.055 40.010 40.904 40.009 40.007
0.620829 41.304 41.304 40.130 40.019 41.304 40.023 40.007
0.858595 41.803 41.803 40.259 40.047 41.803 40.062 40.009
1.15322 42.422 42.422 40.460 40.114 42.422 40.145 40.015
1.52082 43.194 43.194 40.760 40.247 43.194 40.298 40.035
1.972 44.141 44.141 41.189 40.484 44.141 40.548 40.088
[...]
880.907 40.000 40.000 40.022 40.033 40.000 40.050 40.081
899.923 40.000 40.000 40.019 40.029 40.000 40.042 40.068
920.597 40.000 40.000 40.016 40.025 40.000 40.036 40.058
943.115 40.000 40.000 40.014 40.022 40.000 40.031 40.050
967.671 40.000 40.000 40.013 40.020 40.000 40.027 40.043
983.836 40.000 40.000 40.012 40.019 40.000 40.025 40.041
1000 40.000 40.000 40.011 40.018 40.000 40.023 40.038
$ Figure 8: Temperature vs. time at each side of the stainless/carbon steel interface. a — Full time range, b — Zoom around t=100~\text{seconds}
Note: We did not give any initial condition T_0(\vec{x}) so FeenoX decided to start from a steady-state condition, i.e. to solve a static problem with boundary conditions and material properties for t=0 and use that temperature distribution as the initial condition for the transient problem.
The results file written by the WRITE_RESULTS
instruction contains the temperature and heat flux fields at each time
taken by FeenoX. If we wanted to create a smooth animation using
constant time steps, we would need some python programming:
import gmsh
import sys
# time step, i.e. one frame every dt seconds
dt = 1
# argument like $1
if (len(sys.argv) < 2):
n = 1
else:
n = int(sys.argv[1])
# initialize Gmsh
gmsh.initialize(sys.argv)
# read the results written by FeenoX
gmsh.merge("valve-%d.msh" % n)
# set some view options
gmsh.option.setNumber("General.Trackball", 0);
gmsh.option.setNumber("General.RotationX", 290)
gmsh.option.setNumber("General.RotationY", 2)
gmsh.option.setNumber("General.RotationZ", 25)
gmsh.option.setNumber("General.ScaleX", 1.3)
gmsh.option.setNumber("General.ScaleY", 1.3)
gmsh.option.setNumber("General.ScaleZ", 1.3)
gmsh.option.setNumber("Mesh.SurfaceEdges", 0)
gmsh.option.setNumber("Mesh.SurfaceFaces", 0)
gmsh.option.setNumber("Mesh.VolumeFaces", 0)
gmsh.option.setNumber("Mesh.VolumeEdges", 0)
# read original fields
n_steps = int(gmsh.option.getNumber("View[0].NbTimeStep"))
times = []
temps = []
fluxes = []
view_tag_temp = gmsh.view.getTags()[0]
view_tag_flux = gmsh.view.getTags()[1]
for step in range(n_steps):
print(step)
kind_temp, tags_temp, temp, t, n_components = gmsh.view.getModelData(view_tag_temp, step)
temps.append(temp)
kind_flux, tags_flux, flux, t, n_components = gmsh.view.getModelData(view_tag_flux, step)
fluxes.append(flux)
times.append(t)
end_time = t
inst_temp = [0] * len(temp)
view_inst_temp = gmsh.view.add("Temperature transient #%d" % n)
inst_flux = [[0,0,0]] * len(flux)
view_inst_flux = gmsh.view.add("Heat flux transient #%d" % n)
# interpolate the non-constant dt data set to a fixed dt set
t = 0
i = 1
step = 0
while t < end_time:
if t > times[i]:
while times[i] < t:
i += 1
alpha = (t-times[i-1])/(times[i]-times[i-1])
print(t,i,alpha)
for j in range(len(temps[i])):
inst_temp[j] = [temps[i-1][j][0] + alpha * (temps[i][j][0] - temps[i-1][j][0])]
for j in range(len(fluxes[i])):
inst_flux[j] = [fluxes[i-1][j][0] + alpha * (fluxes[i][j][0] - fluxes[i-1][j][0]),
fluxes[i-1][j][1] + alpha * (fluxes[i][j][1] - fluxes[i-1][j][1]),
fluxes[i-1][j][2] + alpha * (fluxes[i][j][2] - fluxes[i-1][j][2])]
gmsh.view.addModelData(view_inst_temp, step, "", kind_temp, tags_temp, inst_temp, t)
gmsh.view.addModelData(view_inst_flux, step, "", kind_flux, tags_flux, inst_flux, t)
step += 1
t += dt
# remove the original fields
gmsh.view.remove(view_tag_temp)
gmsh.view.remove(view_tag_flux)
# initialize the graphical interface
gmsh.fltk.initialize()
# dump each interpolated frame
for i in range(step):
print(i)
gmsh.option.setNumber("View[0].TimeStep", i)
gmsh.option.setNumber("View[1].TimeStep", i)
gmsh.fltk.update()
gmsh.write("valve-temp-%d-%04d.png" % (n,i))
# finalize
gmsh.finalize()
# show instructions to create a video
print("all frames dumped, now run")
print("ffmpeg -y -framerate 10 -f image2 -i valve-temp-%d-%%04d.png valve-temp-%d.mp4" % (n, n))
print("to get a video")
Homework
- Create a new transient #2 and solve it with FeenoX using
$1 = 2.- Replace
WRITE_RESULTSwithWRITE_RESULTS FORMAT vtkand animate the result with ParaView.
4.3 From an arbitrary initial condition with time-dependent BCs
The following input file solves a transient heat conduction equation over a one-dimensional domain x \in [0,L] as discussed in https://www.math.ubc.ca/~peirce/M257_316_2012_Lecture_20.pdf (example 20.2, equation 20.25). The problem has
unitary material properties,
an initial condition identically equal to zero,
a fixed temperature equal to
T(x=0) = \begin{cases} 0 & \text{if $t \leq 1$} \\ A \cdot (t-1) & \text{if $t>1$} \\ \end{cases}
at x=0, and
a fixed temperature equal to zero at x=L.
The analytical solution is a power series
T(x,t) = A \cdot t \left( 1 - \frac{x}{L} \right) + \frac{2 AL^2}{\pi^3 \cdot \kappa^2} \sum_{n=1}^{\infty} \frac{\exp(-\kappa^2 \cdot \left( \frac{n \pi}{L} \right)^2 \cdot t) - 1}{n^3} \sin \left( \frac{n \pi x}{L} \right)
In the following input file we compute the analytical solution up to
n=100. But since the expression blows
up for t<1 we make sure we evaluate
it only for t>1 with the IF
instruction:
# 1D heat transient problem
# from https://www.math.ubc.ca/~peirce/M257_316_2012_Lecture_20.pdf
# (example 20.2, equation 20.25)
# T(0,t) = 0 for t < 1
# A*(t-1) for t > 1
# T(L,t) = 0
# T(x,0) = 0
READ_MESH slab.msh DIMENSIONS 1
PROBLEM thermal
end_time = 2
# unitary non-dimensional properties
k = 1
kappa = 1
# initial condition
T_0(x) = 0
# analytical solution
# example 20.2 equation 20.25
A = 1.23456789
L = 1
N = 100
T_a(x,t) = A*(t-1)*(1-x/L) + 2*A*L^2/(pi^3*kappa^2) * sum((exp(-kappa^2*(i*pi/L)^2*(t-1))-1)/i^3 * sin(i*pi*x/L), i, 1, N)
# boundary conditions
BC left T=if(t>1,A*(t-1),0)
BC right T=0
SOLVE_PROBLEM
IF t>1
PRINT t %.1e T(0.5*L)-T_a(0.5*L,t)
ENDIFgtheler@tom:~/codigos/feenox/doc/tutorials/320-thermal$ feenox thermal-slab-transient.fee
1.00307 9.6e-06
1.00649 1.6e-05
1.01029 2.8e-05
1.01386 4.3e-05
1.02054 7.4e-05
1.02878 1.1e-04
1.03852 1.3e-04
1.05027 1.5e-04
1.06425 1.7e-04
1.08075 1.9e-04
1.10001 2.3e-04
1.12221 2.6e-04
1.14728 3.0e-04
1.17494 3.4e-04
1.20511 4.0e-04
1.23803 4.6e-04
1.27428 5.2e-04
1.31469 5.9e-04
1.36035 6.6e-04
1.41275 7.3e-04
1.47395 8.0e-04
1.54701 8.6e-04
1.63675 9.1e-04
1.75122 9.6e-04
1.87561 9.9e-04
2 1.0e-03
gtheler@tom:~/codigos/feenox/doc/tutorials/320-thermal$