2  Transporte y difusión de neutrones

No debemos tan sólo escribir ni tan sólo leer. Hay que acudir a la vez a lo uno y a lo otro, y combinar ambos ejercicios a fin de que, cuantos pensamientos ha recogido la lectura, los reduzca a la unidad. […] Debemos actuar como las abejas. Las abejas revolotean de aquí para allá y van comiendo en las flores idóneas para elaborar la miel. El botín conseguido lo ordenan y distribuyen por los panales. Te recuerdo que también nosotros tenemos que imitar a las abejas y distinguir cuántas ideas acumulamos de diversas lecturas, pues se conservan mejor diferenciadas. Luego, aplicando la atención y los recursos de nuestro ingenio, debemos fundir en sabor único aquellos diversos jugos de suerte que aún cuando se muestre el modelo del que han sido tomados, no obstante, aparezca distinto de la fuente de inspiración. […] Lo que comprobamos que realiza en nuestro cuerpo la naturaleza sin ninguna colaboración nuestra, es eso lo que tenemos que hacer con la lectura. Los alimentos que tomamos, mientras mantienen su propia cualidad y compactos flotan en el estómago, son una carga. Mas cuando se ha producido su trasformación, entonces y sólo entonces, se convierten en fuerza y sangre. Procuremos otro tanto con los alimentos que nutren nuestro espíritu. No permitamos que queden intactos cuántos hayamos ingerido para que no resulten ajenos a nosotros. Asimilémoslos. De otra suerte, irán al acervo de la memoria y no al de la inteligencia. […] Prestémosle fiel asentimiento y apropiémonos de [lo que leemos] para que resulte una cierta unidad de muchos elementos. […] Aunque se aprecie en ti la semejanza con algún maestro que ha calado profundamente en tu alma por la admiración, quiero que te asemejes a él como un hijo, no como un retrato. […] ¿Cómo lograr esto te preguntas? Con una constante aplicación.

Lucio Séneca, Carta a Lucilio sobre la importancia de escribir, siglo I d.C.

En este capítulo introducimos las ecuaciones que modelan el transporte de neutrones en el núcleo de un reactor nuclear con los siguientes objetivos:

1. Fijar la matemática de las ecuaciones continuas sobre las que se basa la implementación computacional detallada en el capítulo 4 de las ecuaciones de neutrónica discretizadas derivadas en el capítulo 3.
2. Declarar las suposiciones, aproximaciones y limitaciones de los modelos matemáticos utilizados.
3. Definir una nomenclatura consistente para el resto de la tesis, incluyendo los nombres de las variables en el código fuente.

No buscamos explicar los fundamentos físicos de los modelos matemáticos ni realizar una introducción para el lector lego. Para estos casos referimos a las referencias [12], [13] escritas por el autor de esta tesis y a la literatura clásica de física de reactores [3]–[6], [8], [11]. Si bien gran parte del material aquí expuesto ha sido tomado de estas referencias, hay algunos desarrollos matemáticos propios que ayudan a homogeneizar los diferentes enfoques y nomenclaturas existentes en los libros de texto para poder sentar las bases de los esquemas numéricos implementados en el código de manera consistente. Para eso desarrollamos lógica y matemáticamente algunas ideas partiendo de definiciones básicas para arribar a expresiones integro-diferenciales que describen el problema de ingeniería que queremos resolver.

Está claro los desarrollos y ecuaciones expuestos en este capítulo son conocidos desde los albores de la física de reactores allá por mediados del siglo XX. Sin embargo, he decidido volver a deducir una vez más las ecuaciones de transporte y difusión a partir de conceptos de conservación de neutrones manteniendo muchos pasos matemáticos intermedios por dos razones:

1. a modo de escribir una especie de diario estoico como el de Marco Aurelio en el cual digiero (en el sentido de Séneca) la teoría de transporte de neutrones desarrollada a mediados del siglo XX, y
2. abrigando la esperanza de que una condensación homogeneizada¹ de varios libros de neutrónica atraiga estudiantes de grado que estén buscando una fuente de información y que, por contigüidad, éstos aprendan sobre la importancia del software libre y abierto en ingeniería que explico en la Sección 4.4.1.

Para modelar matemáticamente el comportamiento de reactores nucleares de fisión debemos primero poder caracterizar campos de neutrones arbitrarios a través de distribuciones matemáticas sobre un dominio espacial U \in \mathbb{R}^3 de tres dimensiones.² Para ello, vamos a suponer que [8]

1. los neutrones son partículas clásicas, es decir, podemos conocer tanto su posición como su momento con precisión arbitraria independientemente del principio de Heisenberg,
2. los neutrones viajan en línea recta entre colisiones,
3. no existen interacciones neutrón-neutrón,
4. la colisión entre un neutrón incidente y un núcleo blanco es instantánea,
5. las propiedades de los materiales son
   1. continuas en la posición, es decir, la densidad en un diferencial de volumen es uniforme aún cuando sepamos que los materiales están compuestos por átomos individuales, e
   2. isotrópicas, es decir, no hay ninguna dirección preferencial,
6. las propiedades de los núcleos y la composición isotópica de los materiales no dependen del tiempo, y
7. es suficiente que consideremos sólo el valor medio de la distribución de densidad espacial de neutrones y no sus fluctuaciones estadísticas.

Figura 2.1: Un neutrón individual (bola celeste, como todo el mundo sabe), en un cierto tiempo t \in \mathbb{R} está caracterizado por la posición \mathbf{x}\in \mathbb{R}^3 que ocupa en el espacio, por la dirección \hat{\mathbf{\Omega}}= [\Omega_x, \Omega_y, \Omega_z] en la que viaja y por su energía cinética E\in\mathbb{R}. Asumimos que podemos conocer al mismo tiempo la posición \mathbf{x} y su velocidad v\cdot \hat{\mathbf{\Omega}} con precisión arbitraria independientemente del principio de Heisenberg.

En la figura 2.1 ilustramos un neutrón puntual que a un cierto tiempo t está ubicado en una posición espacial \mathbf{x} y se mueve en línea recta en una dirección \hat{\mathbf{\Omega}} con una energía E=1/2 \cdot m v^2.

2.1 Secciones eficaces

Definición 2.1 (sección eficaz macroscópica total) La sección eficaz macroscópica total \Sigma_t de un medio es tal que el producto

\Sigma_t \cdot ds es la probabilidad de que un neutrón tenga una colisión con el núcleo de algún átomo del material por el que viaja a lo largo de una distancia ds en línea recta. Es decir, la sección eficaz macroscópica es el número de colisiones esperadas por neutrón y por unidad de longitud lineal. Sus unidades son inversa de longitud, es decir m^{-1} o cm^{-1}.

Además de referirnos a la sección eficaz³ total, podemos particularizar el concepto al tipo de reacción k, es decir, \Sigma_k \cdot ds es la probabilidad de que un neutrón tenga una reacción de tipo k en el intervalo espacial de longitud ds. En nuestro caso particular, la reacción genérica k puede ser particularizada según el subíndice a

Subíndice	Reacción
t	total
c	captura radiativa
f	fisión
a	absorción (\Sigma_c + \Sigma_f)
s	dispersión (scattering)

Las secciones eficaces macroscópicas dependen de la energía E del neutrón incidente y de las propiedades del medio que provee los núcleos blanco. Como éstas dependen del espacio (usualmente a través de otras propiedades intermedias como por ejemplo temperaturas, densidades o concentraciones de impurezas), en general las secciones eficaces macroscópicas son funciones tanto del espacio \mathbf{x} como de la energía E, es decir \Sigma_k = \Sigma_k(\mathbf{x}, E). En este trabajo no consideramos una dependencia explícita con el tiempo t.

Una forma de incorporar el concepto de sección eficaz macroscópica es pensar que ésta proviene del producto de una sección eficaz microscópica \sigma_k (con unidades de área) y una densidad atómica n (con unidades de inversa de volumen) del medio

\Sigma_k [\text{cm}^{-1}] = \sigma_k [\text{cm}^2] \cdot n [\text{cm}^{-3}]

Figura 2.2: Interpretación de la sección eficaz microscópica como el área asociada a un núcleo transversal a la dirección de viaje del neutrón incidente.

Figura 2.3: Dependencia de la sección eficaz microscópica de absorción \sigma_a con respecto a la energía E del neutrón incidente para diferentes isótopos blanco.

La sección eficaz microscópica \sigma_k tiene efectivamente unidades de área (típicamente del orden de 10^{-24}~\text{cm}^2, unidad que llamamos barn⁴) y se interpreta como el área asociada a un núcleo transversal a la dirección de viaje de un neutrón tal que si este neutrón pasara a través de dicha área, se llevaría a cabo una reacción de tipo k (figura 2.2). Las secciones eficaces microscópicas dependen no solamente de las propiedades nucleares de los núcleos blanco sino que también dependen fuertemente de la energía E del neutrón incidente, llegando a cambiar varios órdenes de magnitud debido a efectos de resonancias como podemos observar en la figura 2.3. Además, \sigma_k depende de la temperatura T del medio que define la forma en la cual los átomos se mueven por agitación térmica alrededor de su posición de equilibrio ya que se produce un efecto tipo Doppler entre el neutrón y el núcleo blanco que modifica la sección eficaz microscópica [14], [15]. Por lo tanto, para un cierto isótopo, \sigma_k = \sigma_k(E,T).

Por otro lado, la densidad atómica n del medio depende de la densidad termodinámica \rho, que a su vez depende de su estado termodinámico usualmente definido por la presión p y la temperatura T. Como estas variables pueden depender de forma arbitraria del espacio \mathbf{x}, podemos escribir efectivamente

\Sigma_k = n \cdot \sigma_k = n \Big( p(\mathbf{x}), T(\mathbf{x}) \Big) \cdot \sigma_k \Big(E, T(\mathbf{x}) \Big) = \Sigma_k (\mathbf{x}, E)

Las ideas presentadas son válidas para un único isótopo libre de cualquier influencia externa. En los reactores nucleares reales, por un lado existen efectos no lineales como por ejemplo el hecho de los átomos de hidrógeno o deuterio y los de oxígeno no están libres en la molécula de agua. Esto hace que las secciones eficaces del todo (i.e. de un conjunto de átomos enlazados covalentemente) no sean iguales a la suma algebraica de las partes y debamos calcular las secciones eficaces macroscópicas con una metodología más apropiada (ver Sección 2.5.1). Por otro lado, justamente en los reactores nucleares las reacciones que interesan son las que dan como resultado la transmutación de materiales por lo que continuamente la densidad atómica n de todos los isótopos varía con el tiempo. En este trabajo, no vamos a tratar con la dependencia de las secciones eficaces con el tiempo explícitamente sino que llegado el caso, como discutimos en la Sección 2.5, daremos la dependencia implícitamente a través de otras propiedades intermedias tales como la evolución del quemado del combustible y/o la concentración de xenón 135 en las pastillas de de dióxido de uranio en forma cuasi-estática.

Observación. Si bien la sección eficaz de un material que es combinación de otros no es la combinación lineal de los componentes, es cierto que las sumas de secciones eficaces correspondientes a reacciones parciales dan como resultado la sección eficaz de la reacción total. Por ejemplo, \Sigma_a = \Sigma_c + \Sigma_f y \Sigma_t = \Sigma_a + \Sigma_s.

A partir de este momento suponemos que conocemos las secciones eficaces macroscópicas en función del vector posición \mathbf{x} y de la energía E para todos los problemas que planteamos, y que además éstas no dependen del tiempo t.

2.1.1 Dispersión de neutrones

Cuando un neutrón que viaja en una cierta dirección \hat{\mathbf{\Omega}} con una energía E colisiona con un núcleo blanco en una reacción de dispersión o scattering,⁵ tanto el neutrón como el núcleo blanco intercambian energía. En este caso podemos pensar que luego de la colisión, el neutrón incidente se ha transformado en otro neutrón emitido en una nueva dirección \hat{\mathbf{\Omega}}^\prime con una nueva energía E^\prime. Para tener este efecto en cuenta, utilizamos el concepto que sigue.

Definición 2.2 (sección eficaz de scattering diferencial) La sección eficaz de scattering diferencial \Sigma_s tal que

\Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime es la probabilidad por unidad de longitud lineal que un neutrón de energía E viajando en la dirección \hat{\mathbf{\Omega}} sea dispersado hacia un intervalo de energía entre E^\prime y E^\prime + dE^\prime y a un cono d\hat{\mathbf{\Omega}}^\prime alrededor de la dirección \hat{\mathbf{\Omega}}^\prime. Sus unidades son inversa de longitud por inversa de ángulo sólido por inversa de energía.

Utilizando argumentos de simetría, podemos mostrar que la sección eficaz diferencial de scattering \Sigma_s sólo puede depender del producto interno \mu = \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{\Omega}}^\prime y no separadamente de \hat{\mathbf{\Omega}} y de \hat{\mathbf{\Omega}}^\prime. En la figura 2.4 ilustramos la idea.

Figura 2.4: Debido a la simetría azimutal, el scattering no depende de las direcciones \hat{\mathbf{\Omega}} y de \hat{\mathbf{\Omega}}^\prime en forma separada sino que depende del coseno del ángulo entre ellas \mu = \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{\Omega}}^\prime.

En general podemos separar a la sección eficaz diferencial (definición 2.2) en una sección eficaz total \Sigma_{s_t} y en una probabilidad de distribución angular y energética \xi_s tal que

\Sigma_s(\mathbf{x}, \mu, E \rightarrow E^\prime) = \Sigma_{s_t}(\mathbf{x}, E) \cdot \xi_s(\mu, E \rightarrow E^\prime) \tag{2.1} donde \Sigma_{s_t} es la sección eficaz macroscópica total de scattering, que da la probabilidad por unidad de longitud de que un neutrón incidente de energía E inicie un proceso de scattering y la función \xi_s describe la distribución de neutrones emergentes.

Podemos integrar ambos miembros de la ecuación 2.1 con respecto a E^\prime y a \mu, y despejar \Sigma_{s_t} para obtener su definición

\Sigma_{s_t}(\mathbf{x}, E) = \frac{\displaystyle \int_{0}^\infty \int_{-1}^{+1} \Sigma_s(\mathbf{x}, \mu, E \rightarrow E^\prime) \, d\mu \, dE^\prime} {\displaystyle \int_{0}^\infty \int_{-1}^{+1} \xi_s(\mu, E \rightarrow E^\prime) \, d\mu \, dE^\prime}

El denominador tiene que ser igual a uno ya que en la reacción de scattering el neutrón dispersado tiene que tener alguna dirección \mu y alguna energía E^\prime. Luego

\Sigma_{s_t}(\mathbf{x}, E) = \int_{0}^\infty \int_{-1}^{+1} \Sigma_s(\mathbf{x}, \mu, E \rightarrow E^\prime) \, d\mu \, dE^\prime \tag{2.2}

2.1.2 Expansión en polinomios de Legendre

Teorema 2.1 (expansión en polinomios de Legendre) Cualquier función f(\mu) : \mu \in [-1,+1] \rightarrow \mathbb{R}^1 de cuadrado integrable puede ser escrita como la suma infinita de un coeficiente f_\ell por el polinomio de Legendre P_{\ell}(\mu) de grado \ell \geq 0

f(\mu) = \sum_{\ell=0}^\infty f_\ell \cdot P_\ell(\mu)

con la condición de normalización

P_\ell(1) = 1

Definición 2.3 Los primeros polinomios de Legendre (figura 2.5) son

\begin{aligned} P_0(\mu) &= 1 \\ P_1(\mu) &= \mu \\ P_2(\mu) &= \frac{1}{2}\left(3 \mu^2-1\right) \\ P_3(\mu) &= \frac{1}{2}\left(5 \mu^3- 3 \mu \right) \\ P_4(\mu) &= \frac{1}{8}\left(35 \mu^4 - 30 \mu^2 + 3 \right) \\ P_5(\mu) &= \frac{1}{8}\left(63 \mu^5 - 70 \mu^3 + 15 \mu \right) \\ P_6(\mu) &= \frac{1}{16}\left(231 \mu^6 - 315 \mu^4 + 105 \mu^2 - 5 \right) \end{aligned}

Figura 2.5: Primeros seis polinomios de Legendre P_\ell(\mu), \ell = 0,\dots,5.

Definición 2.4 (la delta de Kronecker) \delta_{\ell \ell^\prime} = \begin{cases} 1 & \text{si $\ell = \ell^\prime$} \\ 0 & \text{si $\ell \neq \ell^\prime$} \\ \end{cases}

Teorema 2.2 (ortogonalidad de los polinomios de Legendre) Los polinomios de Legendre son ortogonales. Más aún,

\int_{-1}^{+1} P_\ell(\mu) \cdot P_{\ell^\prime}(\mu) \, d\mu = \frac{2}{2\ell + 1} \cdot \delta_{\ell \ell^\prime}

Corolario 2.1 Los coeficientes f_\ell de la expansión de f(\mu) en polinomios de Legendre del teorema 2.1 son iguales a

f_\ell = \frac{2\ell + 1}{2} \cdot \int_{-1}^1 f(\mu) \cdot P_{\ell}(\mu) \, d\mu

Una forma de tener en cuenta la dependencia de \Sigma_s con \mu en la ecuación 2.1 es recurrir a una expansión en polinomios de Legendre. En efecto, para una cierta posición \mathbf{x} y dos energías E y E^\prime fijas, la sección eficaz \Sigma_s de la ecuación 2.1 depende de un único escalar -1 \leq \mu \leq 1 sin presentar singularidades, es decir es una función de cuadrado integrable. Entonces podemos escribir⁶

\Sigma_s(\mathbf{x}, \mu, E \rightarrow E^\prime) = \sum_{\ell=0}^{\infty} \frac{2\ell + 1}{2} \, \Sigma_{s_\ell}(\mathbf{x}, E \rightarrow E^{\prime}) \cdot P_\ell(\mu) \tag{2.3} donde los coeficientes son

\Sigma_{s_\ell}(\mathbf{x}, E\rightarrow E^{\prime}) = \int_{-1}^{+1} \Sigma_s(\mathbf{x}, \mu, E\rightarrow E^\prime) \cdot P_\ell(\mu) \, d\mu \tag{2.4}

Corolario 2.2 La sección eficaz de scattering total \Sigma_{s_t} sólo depende de \Sigma_{s_0}.

Prueba. Reemplazando la expansión dada por la ecuación 2.3 en la ecuación 2.2 tenemos

\begin{aligned} \Sigma_{s_t}(\mathbf{x}, E) &= \int_{0}^{\infty} \int_{-1}^{+1} \sum_{\ell=0}^{\infty} \frac{2\ell + 1}{2} \, \Sigma_{s_\ell}(\mathbf{x}, E \rightarrow E^{\prime}) \cdot P_\ell(\mu) \, d\mu \, dE^\prime \\ &= \int_{0}^{\infty} \left[ \sum_{\ell=0}^{\infty} \frac{2\ell + 1}{2} \, \Sigma_{s_\ell}(\mathbf{x}, E \rightarrow E^{\prime}) \cdot \int_{-1}^{+1} P_\ell(\mu) \, d\mu \right] \, dE^\prime \end{aligned}

Según el teorema 2.2, todos los polinomios de Legendre de orden \ell \geq 1 son ortogonales con respecto a P_0(\mu) = 1, por lo que

\int_{-1}^{+1} P_\ell(\mu) \, d\mu \begin{cases} 2 & \text{para $\ell = 0$} \\ 0 & \text{para $\ell > 0$} \\ \end{cases}

Luego la única contribución a la suma infinita diferente de cero es la correspondiente a \ell=0

\Sigma_{s_t}(\mathbf{x}, E) = \int_{0}^{\infty} \left[ \frac{2 \cdot 0 + 1}{2} \cdot \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^{\prime}) \cdot 2 \right] dE^\prime = \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^{\prime}) dE^\prime \tag{2.5}

Recordando que \mu = \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{\Omega}}^\prime, debe cumplirse que

\int_{4\pi} \Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) \, d\hat{\mathbf{\Omega}}^\prime = \int_{-1}^{+1} \Sigma_s(\mathbf{x},\mu, E \rightarrow E^\prime) \, d\mu \tag{2.6}

Si tenemos scattering isótropo en el marco de referencia del laboratorio,⁷ entonces

1. el integrando del miembro izquierdo de la ecuación 2.6 no depende de \hat{\mathbf{\Omega}}^\prime y puede salir fuera de la integral, y
2. \Sigma_s(\mathbf{x},\mu, E \rightarrow E^\prime) no depende de \mu y el único coeficiente \Sigma_{s_\ell} diferente de cero es el correspondiente a \ell=0 con lo que

\int_{-1}^{+1} \Sigma_s(\mathbf{x},\mu, E \rightarrow E^\prime) \, d\mu = \int_{-1}^{+1} \frac{2\cdot 0 + 1}{2} \cdot \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^\prime) \, d\mu = \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^\prime) \tag{2.7}

Reemplazando la ecuación 2.7 en la 2.6 y sacando \Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) fuera de la integral tenemos

\Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) \cdot 4\pi = \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^\prime) con lo que la sección eficaz diferencial (definición 2.2) para scattering isótropo en el sistema del reactor es igual al coeficiente \Sigma_{s_0} dividido 4\pi

\Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) = \frac{1}{4\pi} \cdot \Sigma_{s_0}(\mathbf{x}, E\rightarrow E^\prime) \tag{2.8}

Observación. Según el punto b y la ecuación 2.3,

\begin{aligned} \Sigma_s(\mathbf{x},\mu, E \rightarrow E^\prime) &= \frac{2\cdot 0 + 1}{2}\cdot \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^\prime) \cdot P_0(\mu) \\ &= \frac{1}{2} \cdot \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^\prime) \end{aligned}

Comparando este resultado con la ecuación 2.8 llegamos a la conclusión que

\Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) = \frac{1}{2\pi} \cdot \Sigma_s(\mathbf{x},\mu, E \rightarrow E^\prime) \tag{2.9}

Este resultado se explica ya que dado un ángulo \hat{\mathbf{\Omega}} fijo, para cada posible valor de \mu hay 2\pi posibles valores de \hat{\mathbf{\Omega}}^\prime que pueden dar como resultado el mismo coseno.

Si en cambio el scattering resulta ser completamente elástico e isótropo pero en el marco de referencia del centro de masa del sistema compuesto por el neutrón incidente y el núcleo blanco, entonces a cada energía de salida E^\prime le corresponde un único ángulo de scattering \mu a través de las leyes clásicas de conservación de energía y momento lineal. Siguiendo el desarrollo de la referencia [11], la sección eficaz diferencial es

\Sigma_s(\mathbf{x}, \mu, E \rightarrow E^\prime) = \begin{cases} \displaystyle \Sigma_{s_t}(\mathbf{x}, E) \cdot \frac{\delta(\mu - \mu_0)}{(1-\alpha)E} & \text{para}~\alpha E < E^\prime < E \\ ~0 ~& \text{de otra manera} \end{cases} donde ahora \delta(x) es la distribución delta de Dirac (no confundir con la \delta de Kronecker de la definición 2.4) y

\alpha(A) = \frac{(A-1)^2}{(A+1)^2}

\mu_0(A,E,E^\prime) = \frac{1}{2} \left[ (A+1)\sqrt{\frac{E^\prime}{E}} - (A-1) \sqrt{\frac{E}{E^\prime}} \right] \tag{2.10} siendo A es el número de masa del núcleo blanco. Llamamos a la magnitud \mu_0 coseno medio de scattering.

Observación. Esta nomenclatura para \mu_0 es general pero la expresión matemática dada por la ecuación 2.10 es particular para el caso de scattering elástico e isótropo en el marco de referencia del centro de masa. En la ecuación 2.12 generalizamos la definición para cualquier tipo de scattering.

La expresión para el \ell-ésimo coeficiente de la expansión en polinomios de Legendre para \alpha E < E^\prime < E según la ecuación 2.4 es

\Sigma_{s_\ell}(\mathbf{x}, E \rightarrow E^\prime) = \frac{\Sigma_{s_t}(\mathbf{x}, E)}{(1-\alpha) E} \int_{-1}^{+1} \delta(\mu - \mu_0) \cdot P_\ell(\mu) \, d\mu = \frac{\Sigma_{s_t}(\mathbf{x}, E) }{(1-\alpha) E} \cdot P_\ell(\mu_0) por lo que

\Sigma_s(\mathbf{x}, \mu, E \rightarrow E^\prime) = \frac{\Sigma_{s_t}(\mathbf{x},E)}{(1 - \alpha) E} \cdot \sum_{\ell=0}^{\infty} \frac{2\ell + 1}{2} \cdot P_\ell(\mu_0) \cdot P_\ell(\mu)

Tomando solamente los dos primeros términos y recordando que P_1(\mu) = \mu, podemos aproximar

\Sigma_s(\mathbf{x}, \mu, E \rightarrow E^\prime) \approx \begin{cases} \frac{\Sigma_{s_t}(\mathbf{x},E)}{(1 - \alpha) E} \cdot \left(1 + \frac{3 \cdot \mu_0 \cdot \mu}{2}\right) & \text{para~$\alpha E < E^\prime < E$} \\ ~0 ~& \text{para~$E^{\prime} < \alpha E$} \end{cases}

Estas dos ideas nos permiten introducir los siguientes conceptos.

Definición 2.5 (scattering isótropo) Decimos que hay scattering isótropo (a partir de ahora siempre nos vamos a referir al marco de referencia del reactor) cuando los coeficientes de la expansión de la sección eficaz diferencial de scattering \Sigma_s(\mathbf{x}, \mu, E \rightarrow E^\prime) en polinomios de Legendre son todos nulos excepto el correspondiente a \ell=0. En este caso, la sección eficaz diferencial no depende del ángulo y vale la ecuación 2.8:

\tag{\ref{eq-sigmas0}} \Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^{\prime}) = \frac{1}{4\pi} \cdot \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^{\prime})

Definición 2.6 (scattering linealmente anisótropo) Si además de \Sigma_{s_0} resulta que el único otro coeficiente diferente de cero es \Sigma_{s_1} correspondiente a \ell=1 entonces decimos que el scattering es linealmente anisótropo, y la sección eficaz diferencial es la suma de la sección eficaz total más un coeficiente multiplicado por el coseno del ángulo de scattering:

\begin{aligned} \Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^{\prime}) &= \frac{1}{4\pi} \cdot \left[ \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^{\prime}) + \left( 2 \cdot 1 + 1 \right) \cdot \Sigma_{s_1}(\mathbf{x}, E \rightarrow E^{\prime}) \cdot P\left(\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{\Omega}}^\prime\right) \right] \\ &= \frac{1}{4\pi} \cdot \left[ \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^{\prime}) + 3 \cdot \Sigma_{s_1}(\mathbf{x}, E \rightarrow E^{\prime}) \cdot \left ( \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{\Omega}}^\prime\right) \right] \end{aligned} \tag{2.11}

Definición 2.7 (coseno medio) Definimos el coseno medio del ángulo de scattering \mu_0 para una ley de dispersión general como

\mu_0(\mathbf{x}, E) = \frac{\displaystyle \int_0^\infty \int_{-1}^{+1} \mu \cdot \Sigma_{s}(\mathbf{x}, \mu, E \rightarrow E^{\prime}) \, d\mu \, dE^\prime} {\displaystyle \int_0^\infty \int_{-1}^{+1} \Sigma_{s}(\mathbf{x}, \mu, E \rightarrow E^{\prime}) \, d\mu \, dE^\prime} = \frac{\displaystyle \int_0^\infty \Sigma_{s_1}(\mathbf{x}, E \rightarrow E^{\prime}) \, dE^\prime} {\displaystyle \int_0^\infty \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^{\prime}) \, dE^\prime} \tag{2.12}

En el caso de scattering general, i.e. no necesariamente isótropo en algún marco de referencia y no necesariamente elástico, debemos conocer entonces

1. la dependencia explícita de \Sigma_s con \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime (que puede ser aproximada mediante evaluaciones discretas), o
2. una cierta cantidad de coeficientes \Sigma_{s_\ell} de su desarrollo en polinomios de Legendre sobre \mu.

En esta tesis trabajamos a lo más con scattering linealmente anisótropo. Esto es, suponemos que la sección eficaz diferencial de scattering está dada por la ecuación 2.11 y suponemos que conocemos tanto \Sigma_{s_0} como \Sigma_{s_1} en función del espacio y de los grupos de energías discretizados antes de resolver la ecuación de transporte a nivel de núcleo (ver Sección 2.5).

2.1.3 Fisión de neutrones

Cuando un núcleo pesado se fisiona en dos núcleos más pequeños, ya sea debido a una fisión espontánea o a una fisión inducida por la absorción de un neutrón, se liberan además de los productos de fisión propiamente dichos y radiación \gamma debida al re-acomodamiento de los niveles energéticos de los nucleones que intervienen en la reacción, entre dos y tres neutrones. Llamamos \nu(\mathbf{x}, E) a la cantidad promedio de neutrones liberados por cada fisión. El valor numérico de 2 < \nu < 3 depende de la energía E del neutrón incidente y de la composición del material combustible el punto \mathbf{x}.

Tal como hicimos en la sección Sección 2.1.1, separamos la probabilidad \Sigma_f de que un neutrón incidente de energía E produzca una fisión unidad de longitud de viaje colisionando con un núcleo blanco en la posición \mathbf{x} en una sección eficaz total \Sigma_{f_t} y una distribución \xi_f en ángulo y energía cada uno de los neutrones nacidos por la fisión

\Sigma_f(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) = \Sigma_{f_t}(\mathbf{x}, E) \cdot \xi_f(\hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime)

La distribución en energía de los neutrones nacidos por fisión está dada por el espectro de fisión \chi, que definimos a continuación.

Definición 2.8 (espectro de fisión) El espectro de fisión \chi(E) es tal que

\chi(E) \, dE es la probabilidad de que un neutrón nacido en una fisión lo haga con una energía dentro del intervalo [E,E+dE]. El espectro de fisión está normalizado de forma tal que

\int_{0}^{\infty} \chi(E) \, dE = 1 \tag{2.13}

Experimentalmente se encuentra que los neutrones de fisión nacen isotrópicamente en el marco de referencia del reactor independientemente de la energía E del neutrón incidente que la provocó. Además, la energía E^\prime con la que emergen tampoco depende de la energía del E neutrón incidente. Luego \xi_f no depende ni de \hat{\mathbf{\Omega}} ni de \hat{\mathbf{\Omega}}^\prime y podemos separarla en una cierta dependencia de \Xi(E) que da la probabilidad de generar una fisión, multiplicada por el espectro de fisión \chi(E^\prime):

\xi_f(\hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) = \Xi(E) \cdot \chi(E^\prime)

Como cada neutrón nacido por fisión tiene que tener alguna dirección de vuelo \hat{\mathbf{\Omega}}^\prime y alguna energía E^\prime, entonces la integral de \xi_f sobre todas las posibles energías E^\prime y ángulos \hat{\mathbf{\Omega}}^\prime debe ser igual a uno. Entonces

\int_0^\infty \int_{4\pi} \xi_f(\hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime = \Xi(E) \cdot \int_0^\infty \int_{4\pi} \chi(E^\prime) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime = 1

Teniendo en cuenta la normalización de \chi dada por la ecuación 2.13, resulta

\Xi(E) = \frac{1}{4\pi} por lo que

\Sigma_f(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) = \frac{\chi(E^\prime)}{4\pi} \cdot \Sigma_{f_t}(\mathbf{x}, E) \tag{2.14}

Observación. Dado que hemos supuesto que la población neutrónica es igual al valor medio de la distribución naturalmente estocástica de los neutrones, desde el punto de vista del desarrollo matemático cada neutrón que produce una fisión genera exactamente \nu(\mathbf{x},E) neutrones de fisión. Como la dependencia de \nu es la misma que la de sección eficaz total de fisión \Sigma_{f_t} entonces englobamos el producto \nu\cdot\Sigma_f como una única función \nu\Sigma_f(\mathbf{x},E).

Durante la operación de un reactor, no todos los neutrones provenientes de la fisión aparecen en el mismo instante en el que se produce. Una cierta fracción \beta de todos los neutrones son producto del decaimiento radioactivo de

1. los productos de fisión, o
2. de los hijos de los productos de fisión.

En cualquier caso, en cálculos transitorios es necesario distinguir entre la fracción 1-\beta de neutrones instantáneos⁸ que aparecen en el mismo momento de la fisión y la fracción \beta de neutrones retardados que aparecen más adelante. Para ello dividimos a los neutrones retardados en I grupos, les asignamos una fracción \beta_i y una constante de tiempo \lambda_i, para i=1,\dots,N y definimos un mecanismo de aparición exponencial para cada uno de ellos.

Como discutimos más adelante en la Sección 3.5, en cálculos estacionarios no es necesario realizar esta división entre neutrones instantáneos y retardados ya que eventualmente todos los neutrones estarán contribuyendo a la reactividad neta del reactor. En el caso particular en el que no haya una fuente externa de neutrones sino que todas las fuentes se deban a fisiones la probabilidad de que el reactor esté exactamente crítico es cero. Para poder realizar cálculos estacionarios y además tener una idea de la distancia a la criticidad debemos recurrir a un reactor crítico asociado, cuya forma más usual es el reactor crítico asociado en k introducido más adelante en la definición 3.27. En este caso, dividimos arbitrariamente las fuentes de fisión por un número real k_\text{eff} \sim 1 que pasa a ser una incógnita del problema y cuya diferencia relativa con respecto a la unidad da una idea de la distancia a la criticidad del reactor original.

2.2 Flujos y ritmos de reacción

El problema central del cálculo de reactores es la determinación de la distribución espacial y temporal de los neutrones dentro del núcleo de un reactor nuclear. En esta sección desarrollamos la matemática para el caso de \mathbf{x} \in \mathbb{R}^3. En casos particulares aclaramos cómo debemos proceder para problemas en una y en dos dimensiones.

Definición 2.9 (densidad de neutrones) La distribución de densidad de neutrones N en un espacio de las fases de siete dimensiones \mathbf{x} \in \mathbb{R}^3, \hat{\mathbf{\Omega}}\in \mathbb{R}^2,⁹ E \in \mathbb{R} y t \in \mathbb{R} tal que

N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} \, d\hat{\mathbf{\Omega}}\, dE

es el número de neutrones (en el sentido de la media estadística dada la naturaleza probabilística del comportamiento de los neutrones) en un elemento volumétrico d^3\mathbf{x} ubicado alrededor del punto \mathbf{x} del espacio viajando en el cono de direcciones de magnitud d\hat{\mathbf{\Omega}} alrededor de la dirección \hat{\mathbf{\Omega}} con energías entre E y E+dE en el tiempo t.¹⁰

Definición 2.10 (flujo angular) El flujo angular \psi es el producto entre la velocidad v y la distribución de densidad N de los neutrones

\begin{aligned} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) &= v(E) \cdot N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \\ &= \sqrt{\frac{2E}{m}} \cdot N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \end{aligned} \tag{2.15} donde v(E) es la velocidad clásica correspondiente a un neutrón de masa m cuya energía cinética es E = 1/2 \cdot mv^2.

Esta magnitud es más útil para evaluar ritmos de colisiones y reacciones que la densidad de neutrones N.

Corolario 2.3 Como v \cdot dt es la distancia lineal ds que viaja un neutrón de velocidad v, entonces

\psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} \, d\hat{\mathbf{\Omega}}\, dE \, dt = v(E) \cdot N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, dt \,\,\, d^3\mathbf{x} \, d\hat{\mathbf{\Omega}}\, dE es el número total de longitudes lineales que los neutrones han viajado sobre un cono d\hat{\mathbf{\Omega}} alrededor de la dirección \hat{\mathbf{\Omega}} con energía en el intervalo [E, E+dE] que estaban en un intervalo de tiempo [t,t+dt] en un diferencial de volumen d^3\mathbf{x} en la posición \mathbf{x}.

Corolario 2.4 La probabilidad de que un neutrón tenga una reacción de tipo k durante la distancia lineal de vuelo ds, según la definición 2.1, es \Sigma_k \cdot ds. Entonces la expresión

\Sigma_k(\mathbf{x}, E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} \, d\hat{\mathbf{\Omega}}\, dE \, dt es el número de reacciones de tipo k en el diferencial de volumen de fases d^3\mathbf{x} \, d\hat{\mathbf{\Omega}}\, dE \, dt.

Para obtener el número total de reacciones de todos los neutrones independientemente de la dirección \hat{\mathbf{\Omega}} del neutrón incidente debemos integrar esta cantidad sobre todos los posibles ángulos de incidencia. Para ello utilizamos el concepto que sigue.

Definición 2.11 (flujo escalar) El flujo escalar \phi es la integral del flujo angular sobre todas las posibles direcciones de viaje de los neutrones:

\phi(\mathbf{x}, E, t) = \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} \tag{2.16}

Corolario 2.5 Con estas definiciones, el ritmo R_k de reacciones de tipo k por unidad de tiempo en d^3\mathbf{x}\,dE es

R_k (\mathbf{x}, E, t) \, d^3\mathbf{x} \, dE = \Sigma_k(\mathbf{x}, E) \cdot \phi(\mathbf{x}, E, t) \, d^3\mathbf{x} \, dE \tag{2.17} con lo que el producto R_t = \Sigma_t \phi da una expresión simple para la distribución del ritmo de reacciones totales por unidad de volumen y de energía.

Definición 2.12 (corriente) El vector corriente \mathbf{J} es la integral del producto entre el flujo angular y el versor de dirección de viaje de los neutrones \hat{\mathbf{\Omega}} sobre todas las direcciones de viaje:

\mathbf{J}(\mathbf{x},E,t) = \int_{4\pi} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\right] \, d\hat{\mathbf{\Omega}}

Observación. La corriente es una cantidad vectorial ya que el integrando es un vector cuya magnitud es igual al flujo angular y cuya dirección es la del versor \hat{\mathbf{\Omega}} sobre el cual estamos integrando.

Observación. El producto escalar entre el vector corriente \mathbf{J} y un cierto versor espacial \hat{\mathbf{n}}

J_n(\mathbf{x}, E, t) = \hat{\mathbf{n}} \cdot \mathbf{J}(\mathbf{x}, E, t) = \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \left( \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} \right) \, d\hat{\mathbf{\Omega}} \tag{2.18} es ahora un escalar que da el número neto de neutrones que cruzan un área unitaria perpendicular a \hat{\mathbf{n}} en la dirección positiva (figura 2.6).

Observación. La cantidad J_n es la resta de dos contribuciones

J_n(\mathbf{x}, E, t) = J_n^+(\mathbf{x}, E, t) - J_n^-(\mathbf{x}, E, t) donde

\begin{aligned} J_n^+(\mathbf{x},E,t) &= + \int_{\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} > 0} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \left(\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}}\right) d\hat{\mathbf{\Omega}}\\ J_n^-(\mathbf{x},E,t) &= - \int_{\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} < 0} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \left(\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}}\right) d\hat{\mathbf{\Omega}} \end{aligned} \tag{2.19}

Figura 2.6: Interpretación del producto del vector corriente \mathbf{J} con el vector normal \hat{\mathbf{n}} a una superficie como el número neto de neutrones que cruzan un área unitaria.

2.3 Transporte de neutrones

Habiendo introducido los conceptos básicos de “contabilidad” de neutrones, pasamos ahora a deducir las ecuaciones que gobiernan sus ritmos de

• aparición,
• desaparición, y
• transporte.

2.3.1 Operador de transporte

Consideremos un volumen finito U\in \mathbb{R}^3 arbitrario fijo en el espacio y consideremos ahora otro volumen U^{\prime}(t)\in \mathbb{R}^3 que se mueve en una dirección fija \hat{\mathbf{\Omega}} con una velocidad constante v(E) correspondiente a una energía E = 1/2 \cdot m v^2 de un neutrón de masa m, de tal manera que en el instante t ambos volúmenes coincidan. En ese momento, la cantidad de neutrones con dirección \hat{\mathbf{\Omega}} en torno al cono definido por d\hat{\mathbf{\Omega}} y con energías entre E y E+dE en el volumen U \equiv U^{\prime}(t) es

N_U(\hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}}\, dE = \left[ \int_{U \equiv U^{\prime}(t)} N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} \right] \, d\hat{\mathbf{\Omega}}\, dE \tag{2.20}

Dado que la posición del dominio de integración cambia con el tiempo, la derivada total de esta magnitud con respecto al tiempo es la suma de una derivada parcial y una derivada material:

\frac{dN_U}{dt} = \frac{\partial N_U}{\partial t} + \lim_{\Delta t \rightarrow 0} \frac{1}{\Delta t} \left[ \int_{U^{\prime}(t+\Delta t)} N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} - \int_{U^{\prime}(t)} N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} \right] \tag{2.21}

Notemos que el dominio U se mueve según

\lim_{\Delta t \rightarrow 0} U^{\prime}(t+\Delta t) = \lim_{\Delta t \rightarrow 0} U^{\prime}(t) + v(E) \cdot \hat{\mathbf{\Omega}}\cdot \Delta t para cada punto \mathbf{x} \in U^{\prime}(t). Además, como ni v(E) ni \hat{\Omega}_i dependen de \mathbf{x} ya que la velocidad es constante y la dirección está fija, entonces el cambio de coordenadas

\mathbf{x}^\prime = \mathbf{x} + v(E) \cdot \hat{\mathbf{\Omega}}\cdot \Delta t

es unitario ya que

\begin{aligned} \frac{\partial}{\partial x} \Big[ x + v(E) \, \hat{\Omega}_x \cdot \Delta t \Big] &= 1 \\ \frac{\partial}{\partial y} \Big[ y + v(E) \, \hat{\Omega}_y \cdot \Delta t \Big] &= 1 \\ \frac{\partial}{\partial z} \Big[ z + v(E) \, \hat{\Omega}_z \cdot \Delta t \Big] &= 1 \end{aligned} y entonces podemos hacer que el dominio de integración de ambas integrales de la ecuación 2.21 coincidan escribiendo

\begin{aligned} \frac{dN_U}{dt} &= \frac{\partial N_U}{\partial t} + \lim_{\Delta t \rightarrow 0} \frac{1}{\Delta t} \left[ \int_{U^{\prime}(t)} N(\mathbf{x}^\prime, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} - \int_{U^{\prime}(t)} N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} \right] \\ &= \frac{\partial N_U}{\partial t} + \lim_{\Delta t \rightarrow 0} \frac{1}{\Delta t} \left[ \int_{U^{\prime}(t)} N(\mathbf{x} + v(E) \cdot \hat{\mathbf{\Omega}}\cdot \Delta t, \hat{\mathbf{\Omega}}, E, t) - N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} \right] \\ \end{aligned}

El segundo término del miembro derecho es igual a v(E) veces la derivada espacial direccional de la función N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) en la dirección \hat{\mathbf{\Omega}}. En efecto, para \hat{\mathbf{\Omega}}, E y t fijos,

\begin{gathered} \lim_{\Delta t \rightarrow 0} N(x + v\cdot\Omega_x\cdot \Delta t, y + v\cdot\Omega_y\cdot \Delta t, z + v\cdot\Omega_y\cdot \Delta t) = \\ \lim_{\Delta t \rightarrow 0} N(x,y,z) + \frac{\partial N}{\partial x} \cdot v \cdot \Omega_x \cdot \Delta t + \frac{\partial N}{\partial y} \cdot v \cdot \Omega_y \cdot \Delta t + \frac{\partial N}{\partial z} \cdot v \cdot \Omega_z \cdot \Delta t \end{gathered}

Reordenando términos y dividiendo por \Delta t

\lim_{\Delta t \rightarrow 0} \frac{1}{\Delta t} \left[ N(\mathbf{x} + v \cdot \hat{\mathbf{\Omega}}\cdot \Delta t) - N(\mathbf{x}) \right] = \text{grad}\left[N(\mathbf{x})\right] \cdot v \cdot \hat{\mathbf{\Omega}}

Como habíamos supuesto que el dominio móvil U^{\prime}(t) coincide con el dominio fijo U en el instante t, es decir U^{\prime}(t) \equiv U, entonces podemos escribir la derivada total de la cantidad de neutrones en U con respecto al tiempo como

\frac{dN_U}{dt} = \frac{\partial N_U}{\partial t} + \int_{U} \hat{\mathbf{\Omega}}\cdot v(E) \cdot \text{grad} \left[ N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] d^3\mathbf{x}

Teniendo en cuenta la ecuación 2.20,

N_U(\hat{\mathbf{\Omega}}, E, t) = \int_{U \equiv U^{\prime}(t)} N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} y la definición 2.10 de flujo angular \psi

\psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = v(E) \cdot N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) tenemos

\frac{d}{dt} \int_{U} N(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d^3\mathbf{x} = \int_{U} \left\{ \frac{1}{v(E)} \frac{\partial \psi}{\partial t} + \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] \right\} d^3\mathbf{x}

Como el dominio U es arbitrario, entonces

\frac{dN}{dt} = \frac{1}{v(E)} \frac{\partial \psi}{\partial t} + \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] \tag{2.22}

Observación. El operador gradiente se aplica sólo sobre las componentes espaciales, es decir

\text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] = \begin{bmatrix} \displaystyle \frac{\partial \psi}{\partial x} \\ \\ \displaystyle \frac{\partial \psi}{\partial y} \\ \\ \displaystyle \frac{\partial \psi}{\partial z} \\ \end{bmatrix} \tag{2.23}

2.3.2 Operador de desapariciones

Cuando un neutrón reacciona con un núcleo blanco, el neutrón incidente puede…

1. ser dispersado, o
2. generar una fisión, o
3. ser capturado por el núcleo blanco.

En los últimos dos casos, el neutrón incidente realmente “desaparece” físicamente. En el caso b, vuelven a nacer \nu(E) neutrones nuevos: una fracción (1-\beta) instantáneamente y \beta en forma retardada durante la cadena de decaimiento de los productos de fisión. En el primer caso, el neutrón incidente nunca desaparece sino que cambia su energía y su dirección de vuelo. De todas maneras, conceptualmente es posible pensar que aún en un proceso de scattering el neutrón incidente de energía E y dirección \hat{\mathbf{\Omega}} desaparece y se emite exactamente un neutrón nuevo con una energía E^\prime y una dirección \hat{\mathbf{\Omega}}^\prime según la ley de scattering de la sección eficaz diferencial \Sigma_s(\mathbf{x},\hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) dada por la definición 2.2.

Con esta idea, cualquier reacción nuclear genera una desaparición del neutrón incidente al mismo tiempo que los casos a y b producen nuevos neutrones. Recordando el corolario 2.5, la tasa o el ritmo de reacciones de cualquier tipo por unidad de volumen y unidad de tiempo es el producto de la sección eficaz total \Sigma_t(\mathbf{x},E) por el flujo escalar \phi(\mathbf{x},E,t). Entonces la tasa de desaparición de neutrones por unidad de volumen y de tiempo es

\Sigma_t(\mathbf{x},E) \cdot \phi(\mathbf{x},E,t) \, d^3\mathbf{x} = \Sigma_t(\mathbf{x},E) \cdot \int_{4\pi} \psi(\mathbf{x},\hat{\mathbf{\Omega}},E,t) \, d\hat{\mathbf{\Omega}}\, d^3\mathbf{x} \tag{2.24}

2.3.3 Operador de producciones

Pasamos ahora a estudiar las posibles maneras en las que pueden aparecer neutrones. Éstos pueden aparecer debido a uno de los siguiente tres mecanismos, que analizamos en las secciones que siguen:

1. scattering,
2. fisión, o
3. fuentes externas.

2.3.3.1 Fuentes por scattering

A la luz de la discusión de la Sección 2.3.2 podemos decir que un neutrón que viajando con una energía E y una dirección \hat{\mathbf{\Omega}} sufre una colisión de scattering en el punto \mathbf{x} es absorbido por el núcleo blanco. Al mismo tiempo, emerge como un nuevo neutrón con una energía E^\prime y una dirección \hat{\mathbf{\Omega}}^\prime. Esta fuente q_s debe ser entonces igual al producto de la probabilidad por unidad de longitud de recorrido de neutrones que viajando en con una energía E en una dirección \hat{\mathbf{\Omega}} colisionen con un núcleo blanco en el punto \mathbf{x} y como resultado adquieren una dirección de viaje \hat{\mathbf{\Omega}}^\prime y una energía E^\prime (recordar los conceptos introducidos en la Sección 2.1.1) por la cantidad de longitudes lineales viajadas, teniendo en cuenta todos los posibles valores de \hat{\mathbf{\Omega}} y de E. Es decir, teniendo en cuenta la definición 2.2 y el corolario 2.3, la fuente de neutrones debida scattering que da como resultado neutrones de energías E^\prime y direcciones \hat{\mathbf{\Omega}}^\prime es

q_s(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) = \int_{0}^{\infty} \int_{4\pi} \Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}}\, dE

Dado que en general estamos interesados en el ritmo en los que los neutrones nacen con energía E y dirección \hat{\mathbf{\Omega}} en el dominio, podemos invertir las variables primadas para obtener la expresión de la fuente de neutrones debidas a scattering por unidad de volumen y de tiempo

q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \int_{0}^{\infty} \int_{4\pi} \Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime\rightarrow \hat{\mathbf{\Omega}}, E^\prime \rightarrow E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime \tag{2.25}

2.3.3.2 Fuentes por fisiones

Ya hemos discutido brevemente en la Sección 2.1.3 (y lo haremos más en detalle en la Sección 3.5), debemos calcular la fuente de fisión ligeramente diferente si estamos resolviendo problemas

1. transitorios
2. estacionarios
   1. con fuentes independientes
   2. sólo con fuentes de fisión

Sin pérdida de generalidad, para fijar ideas supongamos que desde el punto de vista de la fisión el problema es estacionario tanto con fuentes por fisión como con fuentes independientes. De manera análoga a la fuente por scattering, la tasa de generación de neutrones debidas a fisión debido a un neutrón incidente con una dirección \hat{\mathbf{\Omega}} y una energía E es el producto del número probable de nacimientos \nu(E) multiplicada por la probabilidad de que dicho neutrón incidente genere una fisión en el punto \mathbf{x} por unidad de longitud de recorrido multiplicada por la cantidad de longitudes lineales viajadas, teniendo en cuenta todos los posibles valores de direcciones \hat{\mathbf{\Omega}} y energías E incidentes:

q_f(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) = \nu(E) \cdot \int_{0}^{\infty} \int_{4\pi} \Sigma_f(\mathbf{x}, \hat{\mathbf{\Omega}}\rightarrow \hat{\mathbf{\Omega}}^\prime, E \rightarrow E^\prime) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}}\, dE

Recordando la ecuación ecuación 2.14, invirtiendo las variables primadas y escribiendo el producto \nu(E)\cdot\Sigma_{f_t}(\mathbf{x},E) como una única función \nu\Sigma_f(\mathbf{x}.E), tenemos

q_f(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \int_{4\pi} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime \tag{2.26}

2.3.3.3 Fuentes independientes

Por último, para no perder generalidad tenemos que tener en cuenta las fuentes externas de neutrones, es decir aquellas que no provienen de la fisión de materiales presentes en el núcleo sino de otras fuentes totalmente independientes como por ejemplo una fuente de americio-berilio. Matemáticamente, las modelamos como la integral sobre el volumen U de una función arbitraria

s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \tag{2.27}

del espacio, la dirección, la energía y el tiempo que representa la cantidad de neutrones emitidos con energía E en el punto \mathbf{x} con dirección \hat{\mathbf{\Omega}} en el instante t.

2.3.4 La ecuación de transporte

La conservación de neutrones implica que la derivada temporal total de la población de neutrones en la posición \mathbf{x} viajando en la dirección \hat{\mathbf{\Omega}} con una energía E debe ser igual a la diferencia entre la suma de las tres fuentes de las ecuación 2.25 y la tasa de desapariciones ecuación 2.24, tenemos

\begin{gathered} \frac{1}{v} \frac{\partial \psi}{\partial t} + \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] = \\ q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) + q_f(\mathbf{x},\hat{\mathbf{\Omega}}, E, t) + s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) - \Sigma_t(\mathbf{x}, E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \end{gathered} \tag{2.28}

Escribiendo explícitamente los dos términos de fuente por scattering y fisión, pasando el término negativo de desapariciones al miembro izquierdo y teniendo en cuenta que la relación entre velocidad y energía es la clásica E=1/2 \cdot mv^2, llegamos a la famosa ecuación de transporte de neutrones

\begin{gathered} \sqrt{\frac{m}{2E}} \frac{\partial}{\partial t} \Big[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \Big] + \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] + \Sigma_t(\mathbf{x}, E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \\ \int_{0}^{\infty} \int_{4\pi} \Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime\rightarrow \hat{\mathbf{\Omega}}, E^\prime \rightarrow E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime \\ + \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \int_{4\pi} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime + s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \end{gathered} \tag{2.29} que es una ecuación integro-diferencial hiperbólica en derivadas parciales de primer orden tanto sobre el espacio (notar que el operador gradiente opera sólo sobre las coordenadas espaciales \mathbf{x} según la ecuación 2.23) como sobre el tiempo para la incógnita \psi sobre un espacio de fases multidimensional que incluye

1. un dominio espacial U \in \mathbb{R}^3 / \mathbf{x} \in U,
2. el versor dirección \hat{\mathbf{\Omega}}= [\Omega_x, \Omega_y, \Omega_z] / \Omega_x^2 + \Omega_y^2 + \Omega_z^2 = 1,
3. la energía E \in (0,\infty), y
4. el tiempo t \in [0,\infty).

Los datos necesarios para resolver la ecuación de transporte de neutrones son:

• Las secciones eficaces \Sigma_t y \nu\Sigma_f como función del espacio \mathbf{x} y de la energía E^\prime del neutrón incidente.
• El espectro de fisión \chi en función de la energía E del neutrón emitido, en caso de que \nu\Sigma_f \neq 0.
• La sección eficaz diferencial de scattering \Sigma_s como función tanto de la energía E^\prime del neutrón incidente como de la energía E del neutrón saliente, y del ángulo de scattering entre la dirección entrante \hat{\mathbf{\Omega}}^\prime y la dirección saliente \hat{\mathbf{\Omega}}.
  • Esta dependencia es usualmente dada como coeficientes \Sigma_{s_\ell} de la expansión en polinomios de Legendre para \ell=0,\dots,L sobre el escalar \mu = \hat{\mathbf{\Omega}}^\prime\cdot \hat{\mathbf{\Omega}}.
  • Para scattering isótropo en el marco de referencia del reactor, el único coeficiente diferente de cero es \Sigma_{s_0} correspondiente a \ell = 0.
• La fuente independiente de neutrones s como función del espacio \mathbf{x}, la energía E y de la dirección \hat{\mathbf{\Omega}}.
  • Si no hay fuentes externas, este término es cero.
• El parámetro constante m, que es la masa en reposo del neutrón
  • Este parámetro es sólo necesario en cálculos transitorios. Los cálculos estacionarios son independientes de m.

2.3.5 Armónicos esféricos y polinomios de Legendre

Prestemos atención al término de fuente por scattering dado por la ecuación 2.25

\tag{\ref{eq-qs}} q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \int_{0}^{\infty} \int_{4\pi} \Sigma_s(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime\rightarrow \hat{\mathbf{\Omega}}, E^\prime \rightarrow E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime y supongamos que conocemos los coeficientes \Sigma_{s_\ell} de la expansión en polinomios de Legendre de la sección eficaz diferencial de scattering sobre el coseno \mu = \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{\Omega}}^\prime del ángulo de dispersión según la ecuación 2.3

\tag{\ref{eq-sigmas-legendre}} \Sigma_s(\mathbf{x}, \mu, E \rightarrow E^\prime) = \sum_{\ell=0}^{\infty} \frac{2\ell + 1}{2} \, \Sigma_{s_\ell}(\mathbf{x}, E \rightarrow E^{\prime}) \cdot P_\ell(\mu)

Para poder usar estos coeficientes en la fuente de la ecuación 2.25 debemos recordar el resultado de la ecuación 2.9, ya que para cada \mu hay 2\pi posibles ángulos \hat{\mathbf{\Omega}}^\prime:

\begin{aligned} \Sigma_s(\mathbf{x},\hat{\mathbf{\Omega}}^\prime\rightarrow \hat{\mathbf{\Omega}}, E^\prime \rightarrow E) &= \frac{1}{2\pi} \cdot \Sigma_s(\mathbf{x},\mu,E^\prime \rightarrow E) \\ &= \frac{1}{2\pi} \cdot \sum_{\ell=0}^{\infty} \frac{2\ell + 1}{2} \cdot \Sigma_{s_\ell}(\mathbf{x},E^\prime \rightarrow E) \cdot P_\ell(\mu) \end{aligned}

Ahora sí podemos reemplazar esta expansión de \Sigma_s(\mathbf{x},\hat{\mathbf{\Omega}}^\prime\rightarrow \hat{\mathbf{\Omega}}, E^\prime \rightarrow E) en el término de fuentes de la ecuación 2.25,

\begin{aligned} q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) &= \int_{0}^{\infty} \left[ \int_{4\pi} \frac{1}{2\pi} \sum_{\ell=0}^{\infty} \frac{2\ell + 1}{2} \cdot \Sigma_{s_\ell}(\mathbf{x},E^\prime \rightarrow E) \cdot P_\ell(\mu) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) \, d\hat{\mathbf{\Omega}}^\prime\right] dE^\prime\\ & = \int_{0}^{\infty} \sum_{\ell=0}^{\infty} \frac{ 2\ell + 1}{4\pi} \cdot \left[ \Sigma_{s_\ell}(\mathbf{x}, E^{\prime} \rightarrow E) \int_{4\pi} P_\ell(\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{\Omega}}^\prime) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime,t)\, d\hat{\mathbf{\Omega}}^\prime\right] \, dE^{\prime} \end{aligned} \tag{2.30}

Si bien esta expresión ya es suficiente para evaluar el término de scattering cuando tenemos su desarrollo de Legendre, podemos

1. ahondar un poco más en la estructura de la ecuación de transporte, y
2. obtener una expresión computacionalmente más eficiente

expandiendo en una base apropiada el flujo angular \psi, de la misma manera en la que desarrollamos \Sigma_s en una serie de polinomios de Legendre sobre el parámetro \mu.

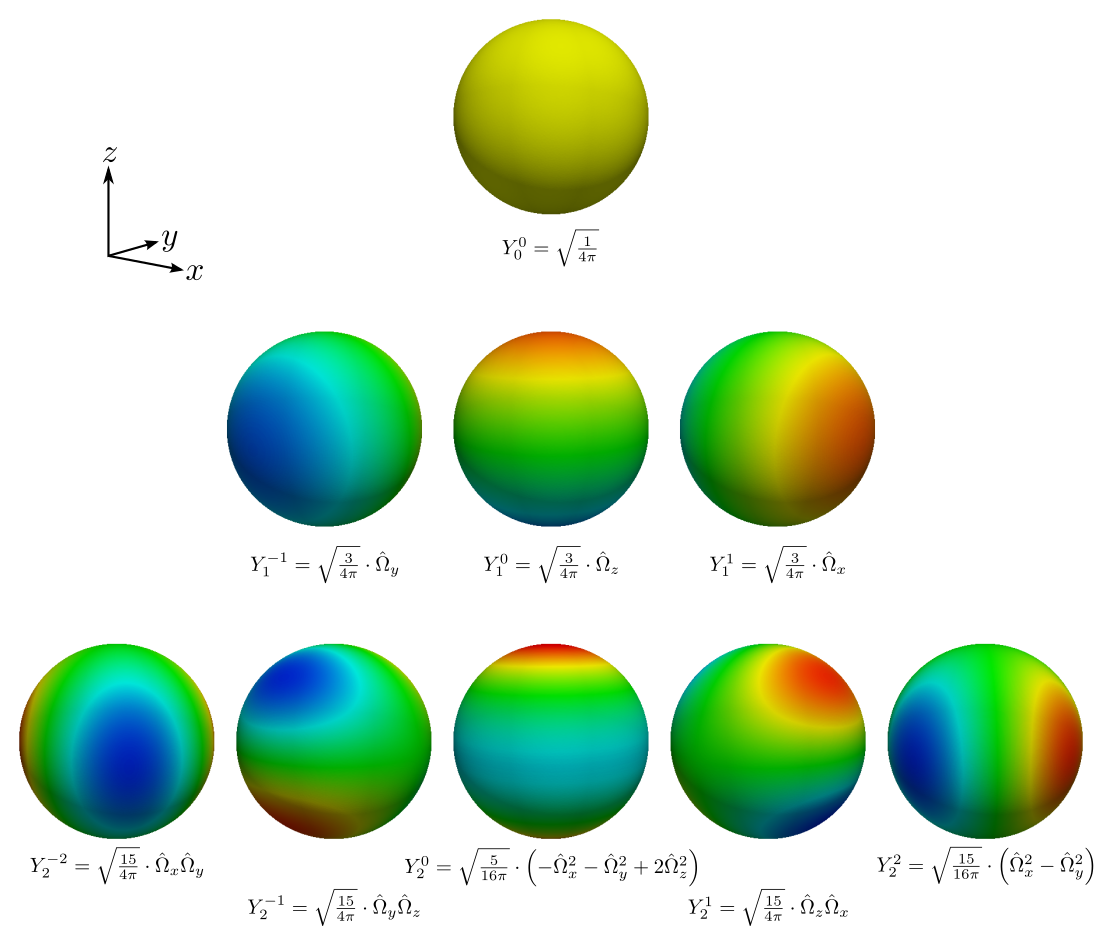
Para ello, notamos que \psi depende angularmente de un versor dirección \hat{\mathbf{\Omega}}= [\hat{\Omega}_x \, \hat{\Omega}_y \, \hat{\Omega}_z]^T (u \hat{\mathbf{\Omega}}^\prime en el caso de la ecuación 2.30). Esta vez, la base de expansión apropiada no son los polinomios de Legendre (que toman un único argumento escalar \mu) sino la generada¹¹ por los armónicos esféricos reales, ilustrados en la figura 2.7.

Teorema 2.3 (expansión en armónicos esféricos reales) Cualquier función f(\hat{\Omega}_x, \hat{\Omega}_y, \hat{\Omega}_z) de cuadrado integrable con

\hat{\Omega}_x^2 + \hat{\Omega}_y^2 + \hat{\Omega}_z^2 = 1 puede ser escrita como la suma doble de un coeficiente f_\ell^m por el armónico esférico normalizado real Y_{\ell}^{m}\left(\hat{\mathbf{\Omega}}\right) de grado \ell \geq 0 y orden m:

f(\hat{\Omega}_x, \hat{\Omega}_y, \hat{\Omega}_z) = \sum_{\ell=0}^\infty \sum_{m=-\ell}^\ell f_\ell^m \cdot Y_\ell^m(\hat{\Omega}_x, \hat{\Omega}_y, \hat{\Omega}_z) donde para cada grado \ell el orden m es tal que

-\ell \leq m \leq \ell

Definición 2.13 Los primeros armónicos esféricos reales (figura 2.7) son

\begin{aligned} Y_0^0(\hat{\Omega}_x,\hat{\Omega}_y,\hat{\Omega}_z) &= \sqrt{\frac{1}{4\pi}} \\ \\ Y_1^{-1}(\hat{\Omega}_x,\hat{\Omega}_y,\hat{\Omega}_z) &= \sqrt{\frac{3}{4\pi}} \cdot \hat{\Omega}_y \\ Y_1^0(\hat{\Omega}_x,\hat{\Omega}_y,\hat{\Omega}_z) &= \sqrt{\frac{3}{4\pi}} \cdot \hat{\Omega}_z \\ Y_1^{+1}(\hat{\Omega}_x,\hat{\Omega}_y,\hat{\Omega}_z) &= \sqrt{\frac{3}{4\pi}} \cdot \hat{\Omega}_x \\ \\ Y_2^{-2}(\hat{\Omega}_x,\hat{\Omega}_y,\hat{\Omega}_z) &= \sqrt{\frac{15}{4\pi}} \cdot \hat{\Omega}_x\cdot\hat{\Omega}_y \\ Y_2^{-1}(\hat{\Omega}_x,\hat{\Omega}_y,\hat{\Omega}_z) &= \sqrt{\frac{15}{4\pi}} \cdot \hat{\Omega}_y\cdot\hat{\Omega}_z \\ Y_2^0(\hat{\Omega}_x,\hat{\Omega}_y,\hat{\Omega}_z) &= \sqrt{\frac{5}{16\pi}} \cdot \left(-\hat{\Omega}_x^2-\hat{\Omega}_y^2+2\cdot\hat{\Omega}_z^2\right) \\ Y_2^{+1}(\hat{\Omega}_x,\hat{\Omega}_y,\hat{\Omega}_z) &= \sqrt{\frac{15}{4\pi}} \cdot \hat{\Omega}_z\cdot\hat{\Omega}_x \\ Y_2^{+2}(\hat{\Omega}_x,\hat{\Omega}_y,\hat{\Omega}_z) &= \sqrt{\frac{15}{16\pi}} \cdot \left(\hat{\Omega}_x^2-\hat{\Omega}_y^2\right) \end{aligned}

Teorema 2.4 (ortonormalidad de los armónicos esféricos reales) Los armónicos esféricos reales son ortonormales, es decir

\int_{4\pi} Y_{\ell}^{m}(\hat{\mathbf{\Omega}}) \cdot Y_{\ell^\prime}^{m^\prime}(\hat{\mathbf{\Omega}}) \, d\hat{\mathbf{\Omega}}= \delta_{\ell \ell^{\prime}} \cdot \delta_{m m^{\prime}} \begin{cases} 1 & \text{si $\ell=\ell^{\prime} \land m=m^{\prime}$} \\ 0 & \text{si $\ell\neq\ell^{\prime} \lor m\neq m^{\prime}$} \end{cases}

Corolario 2.6 Los coeficientes f_\ell^m son iguales a

f_\ell^m (\mathbf{x}, E, t) = \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot Y_{\ell}^{m}(\hat{\mathbf{\Omega}}) \, d\hat{\mathbf{\Omega}}

Teorema 2.5 (de adición) Los armónicos esféricos se relacionan con los polinomios de Legendre como

P_\ell(\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{\Omega}}^\prime) = \frac{4\pi}{2\ell + 1} \sum_{m=-\ell}^{+\ell} Y_\ell^{m}(\hat{\mathbf{\Omega}}) \cdot Y_\ell^m(\hat{\mathbf{\Omega}}^\prime)

Figura 2.7: Representación gráfica de los primeros nueve armónicos esféricos reales (definición 2.13). En la Sección 4.3.1 explicamos cómo generamos esta figura.

Observación. Para \ell = 0 tenemos P_0(\mu) = 1 e Y_0^0(\hat{\mathbf{\Omega}}) = \sqrt{1/4\pi}. En efecto,

P_0(\mu) = 1 = \frac{4\pi}{2\cdot 0 + 1} \cdot \sqrt{\frac{1}{4\pi}} \cdot \sqrt{\frac{1}{4\pi}} = 1

Si en el teorema 2.3 hacemos f igual al flujo angular \psi entonces podemos escribirlo como una suma doble sobre \ell y sobre m del producto de un coeficiente que depende del espacio \mathbf{x}, de la energía E y del tiempo t (pero no de la dirección \hat{\mathbf{\Omega}}) por el armónico esférico de grado \ell y orden m, que no depende ni del espacio \mathbf{x} ni de la energía E ni del tiempo t (pero sí de la dirección \hat{\mathbf{\Omega}}):

\psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E, t) \cdot Y_{\ell}^{m}\left(\hat{\mathbf{\Omega}}\right) \tag{2.31}

Volvamos entonces al término de scattering q_s dado por la ecuación 2.30 y reemplacemos P_\ell(\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{\Omega}}^\prime) en la integral sobre \hat{\mathbf{\Omega}}^\prime por el teorema 2.5:

\begin{gathered} q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \\ \int_{0}^{\infty} \sum_{\ell=0}^{\infty} \frac{ 2\ell + 1}{4\pi} \left[ \Sigma_{s_\ell}(\mathbf{x}, E^{\prime} \rightarrow E) \int_{4\pi} \frac{4\pi}{2\ell + 1} \sum_{m=-\ell}^{+\ell} Y_\ell^m(\hat{\mathbf{\Omega}}) \cdot Y_\ell^m(\hat{\mathbf{\Omega}}^\prime) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime,t)\, d\hat{\mathbf{\Omega}}^\prime\right] dE^{\prime} \\ = \int_{0}^\infty \sum_{\ell=0}^\infty \left[ \Sigma_{s_\ell}(\mathbf{x}, E^{\prime} \rightarrow E) \sum_{m=-\ell}^{+\ell} Y_\ell^{m}(\hat{\mathbf{\Omega}}) \int_{4\pi} Y_\ell^m(\hat{\mathbf{\Omega}}^\prime) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime,E^\prime,t)\, d\hat{\mathbf{\Omega}}^\prime\right] dE^{\prime} \end{gathered}

La integral sobre d\hat{\mathbf{\Omega}}^\prime dentro del corchete es justamente el coeficiente \Psi_\ell^m de la expansión en armónicos esféricos del flujo angular \psi dado por el corolario 2.6. Luego

q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \int_{0}^{\infty} \sum_{\ell=0}^\infty \left[ \Sigma_{s_\ell}(\mathbf{x}, E^{\prime} \rightarrow E) \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E^{\prime}, t) \cdot Y_\ell^{m}(\hat{\mathbf{\Omega}}) \right] \, dE^{\prime} \tag{2.32}

Esta ecuación 2.32 refleja la forma en la que incide la fuente de scattering en el balance global de neutrones: el modo \ell de la expansión en polinomios de Legendre de la sección diferencial \Sigma_s de scattering contribuye sólo a través de los modos de grado \ell de la expansión en armónicos esféricos del flujo angular \psi. En particular, para scattering isótropo sólo el término para \ell=0 y m=0 contribuye a la fuente de scattering q_s. De la misma manera, para scattering linealmente anisótropo además sólo contribuyen los tres términos con \ell=1 y m=-1,0,+1.

Prestemos atención ahora al coeficiente \Psi_0^0. Ya que por un lado Y_0^0 = \sqrt{1/4\pi} (definición 2.13) mientras que por otro la integral del flujo angular \psi con respecto a \hat{\mathbf{\Omega}} sobre todas las direcciones es igual al flujo escalar (definición 2.11), entonces

\Psi_0^0(\mathbf{x}, E, t) = \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E,t) \cdot Y_0^0(\hat{\mathbf{\Omega}}) \, d\hat{\mathbf{\Omega}}= \sqrt{\frac{1}{4\pi}} \cdot \phi(\mathbf{x}, E, t)

De esta manera, podemos escribir la suma de la ecuación 2.31 con el primer término de la expansión del flujo angular \psi escrito explícitamente como

\begin{aligned} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) &= \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E, t) \cdot Y_{\ell}^{m} ({\hat{\mathbf{\Omega}}}) \\ &= \sqrt{\frac{1}{4\pi}} \cdot \phi(\mathbf{x}, E, t) \cdot \sqrt{\frac{1}{4\pi}} + \sum_{\ell=1}^{\infty} \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E, t) \cdot Y_{\ell}^{m} ({\hat{\mathbf{\Omega}}}) \\ &= \frac{\phi(\mathbf{x}, E, t)}{4\pi} + \sum_{\ell=1}^{\infty} \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E, t) \cdot Y_{\ell}^{m} ({\hat{\mathbf{\Omega}}}) \end{aligned}

Más aún, según la definición 2.13, los coeficientes de grado \ell=1 son

\begin{aligned} \Psi_1^{-1}(\mathbf{x}, E, t) &= \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E,t) \cdot \textstyle \sqrt{\frac{3}{4\pi}} \cdot \hat{\Omega}_y \, d\hat{\mathbf{\Omega}}= \sqrt{\frac{3}{4\pi}} \cdot J_y(\mathbf{x}, E, t) \\ \Psi_1^{0}(\mathbf{x}, E, t) &= \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E,t) \cdot \textstyle \sqrt{\frac{3}{4\pi}} \cdot \hat{\Omega}_z \, d\hat{\mathbf{\Omega}}= \sqrt{\frac{3}{4\pi}} \cdot J_z(\mathbf{x}, E, t) \\ \Psi_1^{1+}(\mathbf{x}, E, t) &= \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E,t) \cdot \textstyle \sqrt{\frac{3}{4\pi}} \cdot \hat{\Omega}_x \, d\hat{\mathbf{\Omega}}= \sqrt{\frac{3}{4\pi}} \cdot J_x(\mathbf{x}, E, t) \\ \end{aligned} donde en la última igualdad hemos empleado la definición 2.12 del vector corriente

\mathbf{J}(\mathbf{x},E,t) = \int_{4\pi} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\right] \, d\hat{\mathbf{\Omega}} = \begin{bmatrix} J_x \\ J_y \\ J_z \end{bmatrix} y la ecuación 2.18.

Observación. El vector corriente \mathbf{J}(\mathbf{x},E,t) depende del espacio \mathbf{x}, la energía E y el tiempo t pero no del ángulo \hat{\mathbf{\Omega}}.

Podemos escribir también los tres términos correspondiente a \ell=1 de la expansión del flujo angular \psi explícitamente como tres veces (sobre 4\pi) el producto interno entre el vector corriente \mathbf{J}(\mathbf{x},E,t) y la dirección \hat{\mathbf{\Omega}} de forma tal que

\begin{aligned} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) &= \frac{\phi(\mathbf{x}, E, t)}{4\pi} + \sum_{\ell=1}^{\infty} \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E, t) \cdot Y_{\ell}^{m} ({\hat{\mathbf{\Omega}}}) \\ &= \frac{1}{4\pi} \left[ \phi(\mathbf{x}, E, t) + 3 \cdot \left(\mathbf{J}(\mathbf{x}, E, t) \cdot \hat{\mathbf{\Omega}}\right) \right] + \sum_{\ell=2}^{\infty} \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E, t) \cdot Y_{\ell}^{m} ({\hat{\mathbf{\Omega}}}) \end{aligned} \tag{2.33}

Como comprobación, verificamos que a partir de esta expresión podemos recuperar el flujo escalar integrando con respecto a \hat{\mathbf{\Omega}} sobre 4\pi

\begin{aligned} \phi(\mathbf{x},E,t) &= \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}}\\ &= \frac{1}{4\pi} \int_{4\pi} \left[ \phi(\mathbf{x},E,t) + \left( 3\cdot \mathbf{J}(\mathbf{x},E,t) \cdot \hat{\mathbf{\Omega}}\right) + \sum_{\ell=2}^{\infty} \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E, t) \cdot Y_{\ell}^{m} ({\hat{\mathbf{\Omega}}}) \right] \, d\hat{\mathbf{\Omega}} \end{aligned} \tag{2.34}

Por un lado, la integral del segundo término 3 (\mathbf{J} \cdot \hat{\mathbf{\Omega}}) sobre d\hat{\mathbf{\Omega}} es cero. En efecto,

\int_{4\pi} 3 \cdot \mathbf{J}(\mathbf{x},E,t) \cdot \hat{\mathbf{\Omega}}\, d\hat{\mathbf{\Omega}} = 3\cdot \mathbf{J}(\mathbf{x},E,t) \cdot \int_{4\pi} \hat{\mathbf{\Omega}}\, d\hat{\mathbf{\Omega}} = 3\cdot \mathbf{J}(\mathbf{x},E,t) \int_{4\pi} \begin{bmatrix} \Omega_x \\ \Omega_y \\ \Omega_z \end{bmatrix} \, d\hat{\mathbf{\Omega}} = 0

Para analizar los siguientes términos para \ell \geq 2 necesitamos tener en cuenta el siguiente teorema.

Teorema 2.6 La integral sobre la esfera unitaria del armónico esférico Y_\ell^m de grado \ell y orden m es

\int_{4\pi} Y_\ell^m(\hat{\mathbf{\Omega}}) \, d\hat{\mathbf{\Omega}}= \begin{cases} \sqrt{4\pi} & \text{para $\ell=0 \land m=0$} \\ 0 & \text{de otra manera} \end{cases}

Prueba. Tomemos \ell^\prime = 0 y m^\prime=0 en el teorema 2.4 y reemplacemos la definición 2.13 para Y_0^0 = 1/\sqrt{4\pi}

\begin{aligned} \int_{4\pi} Y_{\ell}^{m}(\hat{\mathbf{\Omega}}) \cdot Y_{0}^{0}(\hat{\mathbf{\Omega}}) \, d\hat{\mathbf{\Omega}}&= \delta_{\ell 0} \delta_{m 0} \\ \int_{4\pi} Y_{\ell}^{m}(\hat{\mathbf{\Omega}}) \cdot \sqrt{\frac{1}{4\pi}}\, d\hat{\mathbf{\Omega}}&= \delta_{\ell 0} \delta_{m 0} \\ \int_{4\pi} Y_{\ell}^{m}(\hat{\mathbf{\Omega}}) \, d\hat{\mathbf{\Omega}}&= \sqrt{4\pi} \cdot \delta_{\ell 0} \cdot \delta_{m 0} \end{aligned}

En virtud del teorema 2.6, los términos de la sumatoria sobre \ell \geq 2 en la ecuación 2.34 tampoco contribuyen a la integral por lo que

\phi(\mathbf{x},E,t) = \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}}= \frac{1}{4\pi} \int_{4\pi} \phi(\mathbf{x},E,t) \, d\hat{\mathbf{\Omega}}= \phi(\mathbf{x},E,t)

Teorema 2.7 La integral del producto de dos cosenos dirección individuales \int_{4\pi} \hat{\Omega}_i \cdot \hat{\Omega}_j \, d\hat{\mathbf{\Omega}}= \frac{4\pi}{3} \cdot \delta_{ij} para i=x,y,z y j=x,y,z.

Teorema 2.8 La integral del producto de una cantidad impar de cosenos es cero \int_{4\pi} \hat{\Omega}_x^r \cdot \hat{\Omega}_y^s \cdot \hat{\Omega}_z^t \, d\hat{\mathbf{\Omega}}= 0 \quad \text{si $r$, $s$ o $t$ es impar}

Podemos demostrar entonces que con la definición 2.12 recuperamos además el vector corriente.

Prueba. En efecto,

\begin{aligned} \mathbf{J}(\mathbf{x},E,t) &= \int_{4\pi} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\right] \, d\hat{\mathbf{\Omega}}\\ &= \frac{1}{4\pi} \int_{4\pi} \Big\{ \phi(\mathbf{x}, E,t) \cdot \hat{\mathbf{\Omega}}+ 3 \cdot \left[ \mathbf{J}(\mathbf{x},E,t) \cdot \hat{\mathbf{\Omega}}\right] \cdot \hat{\mathbf{\Omega}}\\ & \quad\quad\quad\quad\quad\quad\quad + \sum_{\ell=2}^{\infty} \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E, t) \cdot \left[ Y_{\ell}^{m}(\hat{\mathbf{\Omega}}) \cdot \hat{\mathbf{\Omega}}\right] \Big\} \, d\hat{\mathbf{\Omega}} \end{aligned} \tag{2.35}

El primer término \phi \cdot \hat{\mathbf{\Omega}} se anula porque por un lado \phi no depende de \hat{\mathbf{\Omega}} y por otro, como ya demostramos, \int_{4\pi} \hat{\mathbf{\Omega}}\,d\hat{\mathbf{\Omega}}= 0. Pero además los factores Y_\ell^m \cdot \hat{\mathbf{\Omega}} dentro de la sumatoria doble también se anulan porque cualquier armónico Y_\ell^m con \ell>1 es ortogonal con respecto a los tres armónicos Y_1^m de orden \ell=1, que a su vez son proporcionales a \hat{\mathbf{\Omega}}:

\begin{bmatrix} Y_1^{+1}(\hat{\mathbf{\Omega}}) \\ Y_1^{-1}(\hat{\mathbf{\Omega}}) \\ Y_1^{0}(\hat{\mathbf{\Omega}}) \\ \end{bmatrix} = \sqrt{\frac{3}{4\pi}} \cdot \begin{bmatrix} \hat{\Omega}_x \\ \hat{\Omega}_y \\ \hat{\Omega}_z \\ \end{bmatrix} = \sqrt{\frac{3}{4\pi}} \cdot \hat{\mathbf{\Omega}} \tag{2.36}

Entonces

\begin{aligned} \mathbf{J}(\mathbf{x},E,t) &= \frac{3}{4\pi} \int_{4\pi} \left( J_x \hat{\Omega}_x + J_y \hat{\Omega}_y + J_z \hat{\Omega}_z \right) \cdot \begin{bmatrix} \hat{\Omega}_x \\ \hat{\Omega}_y \\ \hat{\Omega}_z \end{bmatrix} \, d\hat{\mathbf{\Omega}}\\ &= \frac{3}{4\pi} \int_{4\pi} \begin{bmatrix} J_x \hat{\Omega}_x \hat{\Omega}_x + J_y \hat{\Omega}_y \hat{\Omega}_x + J_z \hat{\Omega}_z \hat{\Omega}_x \\ J_x \hat{\Omega}_x \hat{\Omega}_y + J_y \hat{\Omega}_y \hat{\Omega}_y + J_z \hat{\Omega}_z \hat{\Omega}_y \\ J_x \hat{\Omega}_x \hat{\Omega}_z + J_y \hat{\Omega}_y \hat{\Omega}_z + J_z \hat{\Omega}_z \hat{\Omega}_z \end{bmatrix} \, d\hat{\mathbf{\Omega}}\\ \end{aligned}

Usando el teorema 2.7,

\begin{aligned} \mathbf{J}(\mathbf{x},E,t) &= \frac{3}{4\pi} \int_{4\pi} \begin{bmatrix} J_x \cdot \frac{4\pi}{3} + J_y \cdot 0 + J_z \cdot 0 \\ J_x \cdot 0 + J_y \cdot \frac{4\pi}{3} + J_z \cdot 0 \\ J_x \cdot 0 + J_y \cdot 0 + J_z \cdot \frac{4\pi}{3} \end{bmatrix} \, d\hat{\mathbf{\Omega}}\\ &= \frac{3}{4\pi} \int_{4\pi} \begin{bmatrix} \frac{4\pi}{3} J_x \\ \frac{4\pi}{3} J_y \\ \frac{4\pi}{3} J_z \\ \end{bmatrix} \, d\hat{\mathbf{\Omega}}\\ &= \mathbf{J}(\mathbf{x},E,t) \end{aligned} que es lo que queríamos demostrar.

Volviendo a la evaluación del término de scattering, aprovechando el hecho de que la ecuación 2.33 nos da una forma particular para el flujo angular en función de los dos modos \ell=0 y \ell=1, podemos calcular la fuente de scattering q_s dada por la ecuación 2.32 como

\begin{gathered} q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \frac{1}{4\pi} \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \phi(\mathbf{x}, E^{\prime}, t) \, dE^\prime \\ + \frac{3}{4\pi} \int_{0}^{\infty} \Sigma_{s_1}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \left(\mathbf{J}(\mathbf{x},E^{\prime},t) \cdot \hat{\mathbf{\Omega}}\right) \, dE^\prime \\ + \sum_{\ell=2}^\infty \int_{0}^{\infty} \left[ \Sigma_{s_\ell}(\mathbf{x}, E^{\prime} \rightarrow E) \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E^{\prime}, t) \cdot Y_\ell^{m}(\hat{\mathbf{\Omega}}) \right] \, dE^{\prime} \end{gathered} \tag{2.37} que es una ecuación mucho más útil—desde el punto de vista computacional—que la ecuación 2.25, que da un expresión demasiado general y muy difícil de evaluar. Esto es especialmente importante si podemos despreciar los términos para \ell>1 y suponer a lo más scattering linealmente anisótropo (definición 2.6). En este caso entonces

\begin{gathered} q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \frac{1}{4\pi} \left\{ \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \phi(\mathbf{x}, E^{\prime}, t) \, dE^\prime \right. \\ \left. + 3 \cdot \int_{0}^{\infty} \Sigma_{s_1}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \left[\mathbf{J}(\mathbf{x},E^{\prime},t) \cdot \hat{\mathbf{\Omega}}\right] \, dE^\prime \right\} \end{gathered} \tag{2.38}

Más aún, para el caso particular de scattering isótropo (definición 2.5), q_s se reduce a

\begin{gathered} q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \frac{1}{4\pi} \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \phi(\mathbf{x}, E^{\prime}, t) \, dE^\prime \end{gathered} \tag{2.39}

Para completar la sección, notamos que dado que la fuente de neutrones debida a fisiones se asume isótropa en el marco de referencia del reactor, su evaluación es similar a esta última ecuación 2.39. En efecto, el término de fisiones de la ecuación de transporte ecuación 2.29 es

q_f(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \int_{4\pi} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime

El coeficiente \nu\Sigma_f no depende de \hat{\mathbf{\Omega}}^\prime por lo que puede salir fuera de la integral sobre 4\pi. Recordando la definición 2.11 de \phi resulta

\begin{aligned} q_f(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) &= \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^\prime, t) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime \\ &= \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \phi(\mathbf{x}, E^\prime, t) \, dE^\prime \end{aligned} \tag{2.40}

Observación. Ni la ecuación 2.39 ni la ecuación 2.40 dependen de la dirección \hat{\mathbf{\Omega}}.

2.3.6 Transporte linealmente anisótropo en estado estacionario

En esta tesis hacemos foco en el caso

1. estacionario, y
2. con scattering linealmente anisótropo (a lo más)

En estas condiciones, la ecuación de transporte queda

\begin{gathered} \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E) \right] + \Sigma_t(\mathbf{x}, E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E) = \\ \frac{1}{4\pi} \cdot \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^{\prime}) \, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime + \\ \frac{3 \cdot \hat{\mathbf{\Omega}}}{4\pi} \cdot \int_{0}^{\infty} \Sigma_{s_1}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}^\prime, E^{\prime}) \cdot \hat{\mathbf{\Omega}}^\prime\, d\hat{\mathbf{\Omega}}^\prime\, dE^\prime \\ + \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \phi(\mathbf{x}, E^\prime) \, dE^\prime + s(\mathbf{x}, \hat{\mathbf{\Omega}}, E) \end{gathered} \tag{2.41}

Si el scattering es isótropo entonces \Sigma_{s_1}=0 y el segundo término del miembro derecho se anula.

2.3.7 Condiciones iniciales y de contorno

Como ya hemos mencionado en la Sección 2.3.4 luego de introducir la ecuación 2.29, la ecuación de transporte es una ecuación integro-diferencial en derivadas parciales de primer orden sobre las coordenadas espaciales \mathbf{x} en un cierto dominio espacial U \in \mathbb{R}^3 y una derivada temporal de primer orden sobre t \in [0,\infty]. Luego debemos dar condiciones de contorno \psi(\mathbf{x}=\partial U,E,\hat{\mathbf{\Omega}}=\hat{\mathbf{\Omega}}^{*},t) sobre la frontera \partial U del dominio U también para todas las energías E y tiempos t pero no para todas las direcciones \hat{\mathbf{\Omega}} sino para un subconjunto \hat{\mathbf{\Omega}}^{*} ya que la ecuación es de primer orden. Esto es, para cada punto \mathbf{x} \in \partial U sólo se debe fijar el flujo angular \psi correspondiente a las direcciones \hat{\mathbf{\Omega}}^{*} que entren al dominio U, es decir tal que el producto interno \hat{\mathbf{\Omega}}^{*} \cdot \hat{\mathbf{n}} < 0, donde \hat{\mathbf{n}} es el vector normal externo a la frontera \partial U en el punto \mathbf{x}. En forma equivalente, se puede pensar como que el flujo angular \psi puede estar fijado, para cada dirección, a lo más en un único punto del espacio ya que la ecuación es de primer grado. Si estuviese fijado en dos puntos, el problema matemático estaría mal definido, como ilustramos en la figura 2.8.

Figura 2.8: Para una dirección \hat{\mathbf{\Omega}} fija, la ecuación de transporte es una ecuación diferencial de primer orden sobre el espacio. Matemáticamente, esta ecuación puede tener una única condición de contorno o bien en el punto A o bien en el punto B, pero no en ambos. Físicamente, sólo tiene sentido que la condición esté sobre el punto A ya que la dirección \hat{\mathbf{\Omega}} entra al dominio U.

Definición 2.14 (condición de contorno de vacío) Llamamos condición de contorno de vacío a la situación en la cual todos los flujos angulares entrantes a U son nulos:

\psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = 0 \quad\quad \forall \mathbf{x} \in \Gamma_V \subset \partial U \land \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}}(\mathbf{x}) < 0

Para cada dirección entrante \hat{\mathbf{\Omega}}/ \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} < 0 definimos el conjunto \Gamma_V \subset \partial U como el lugar geométrico de todos los puntos \mathbf{x} donde imponemos esta condición de contorno.

Definición 2.15 (condición de contorno de espejo) Llamamos condición de contorno de reflexión o de simetría o tipo espejo cuando el flujo angular entrante en el punto \mathbf{x} \in \partial U es igual al flujo angular saliente en la dirección reflejada

\hat{\mathbf{\Omega}}^\prime= \hat{\mathbf{\Omega}}- 2 \left( \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} \right) \hat{\mathbf{n}} \tag{2.42}

con respecto a la normal exterior \hat{\mathbf{n}}(\mathbf{x}) (figura 2.9)

\psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \psi\left[\mathbf{x}, \hat{\mathbf{\Omega}}- 2 \left( \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} \right) \hat{\mathbf{n}}, E, t\right] \quad\quad \forall \mathbf{x} \in \Gamma_M \subset \partial U \land \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}}(\mathbf{x}) < 0

Definimos el conjunto \Gamma_M \subset \partial U como el lugar geométrico de todos los puntos \mathbf{x} donde imponemos esta condición de contorno.

Figura 2.9: La dirección reflejada \hat{\mathbf{\Omega}}^\prime de la dirección incidente con respecto a la normal exterior \hat{\mathbf{n}} al dominio U en el punto de la frontera \mathbf{x} \in \partial U. Se cumple que \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} = -\hat{\mathbf{\Omega}}^\prime\cdot \hat{\mathbf{n}}.

Las dos condiciones de contorno dadas en la definición 2.14 y en la definición 2.15 son de tipo Dirichlet ya que se fija el valor de la incógnita \psi. Además ambas son homogéneas porque el valor fijado es igual a cero.

Definición 2.16 Si

1. las fuentes de fisión son idénticamente nulas, o
2. las fuentes de fisión son no nulas y las fuentes independientes también son no nulas

entonces es posible tener una condición de contorno general de Dirichlet no homogénea

\psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \psi_\Gamma(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \neq 0 \quad\quad \forall \mathbf{x} \in \Gamma_{I} \not\subset \left(\Gamma_V \cup \Gamma_M\right) \land \hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}}(\mathbf{x}) < 0

Definimos el conjunto \Gamma_I \subset \partial U como el lugar geométrico de todos los puntos \mathbf{x} donde imponemos esta condición de contorno.

Observación. Los problemas estacionarios en los cuales la única fuente de neutrones proviene de fisiones no admiten condiciones de contorno inhomogéneas.

2.4 Aproximación de difusión

La ecuación de difusión de neutrones es una aproximación muy útil que permite

1. obtener soluciones analíticas aproximadas en algunas geometrías simples, y
2. transformar una ecuación diferencial hiperbólica de primer orden en una elíptica de segundo orden sin dependencia angular explícita, simplificando sensiblemente las soluciones numéricas debido a que
   1. la ecuación de difusión discretizada presenta mucho menos grados de libertad que otras formulaciones, tales como ordenadas discretas, y
   2. la discretización numérica del operador elíptico deviene en matrices simétricas y definidas positivas que permiten la aplicación de algoritmos de resolución muy eficientes, tales como los métodos multi-grid [2], [9].

En esta sección derivamos la ecuación de difusión a partir de la ecuación de transporte. La segunda puede ser considerada exacta en el sentido de que todas las deducciones lógicas e igualdades entre miembros han sido estrictas, si damos por cierto las siete suposiciones. La primera es una aproximación que, como mostramos en esta sección, proviene de igualar la corriente \mathbf{J} en forma aproximada a un coeficiente negativo por el gradiente \nabla \phi del flujo escalar despreciando la contribución de los términos con \ell \geq 2 en la expansión en armónicos esféricos del flujo angular \psi.

2.4.1 Momento de orden cero

Comenzamos integrando la ecuación de transporte de neutrones 2.28 sobre todas los direcciones \hat{\mathbf{\Omega}} para obtener

\begin{gathered} \int_{4\pi} \frac{1}{v} \frac{\partial}{\partial t} \Big[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \Big] \, d\hat{\mathbf{\Omega}} + \int_{4\pi} \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] \, d\hat{\mathbf{\Omega}}\\ + \int_{4\pi} \Sigma_t(\mathbf{x}, E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} = \int_{4\pi} q(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} \end{gathered} \tag{2.43}

Teorema 2.9 (extensión de la regla de la derivada del producto) La divergencia del producto entre el escalar a(\mathbf{x}) y el vector \mathbf{b(\mathbf{x})} es

\mathrm{div} \big[ a(\mathbf{x}) \cdot \mathbf{b}(\mathbf{x}) \big ] = a(\mathbf{x}) \cdot \mathrm{div} \left[\mathbf{b}(\mathbf{x})\right] + \mathbf{b}(\mathbf{x}) \cdot \mathrm{grad}\left[a(\mathbf{x})\right]

Corolario 2.7 Para a=\psi y \mathbf{b} =\hat{\mathbf{\Omega}} y el escalar \psi,

\mathrm{div} \left(\hat{\mathbf{\Omega}}\cdot \psi \right) = \hat{\mathbf{\Omega}}\cdot \mathrm{grad} \left( \psi \right) + \psi \cdot \mathrm{div} ( \hat{\mathbf{\Omega}})

Por la ecuación 2.23 el operador diferencial actúa solamente sobre las coordenadas espaciales. Entonces \text{div} ( \hat{\mathbf{\Omega}}) = 0. Luego

\mathrm{div}\left(\hat{\mathbf{\Omega}}\cdot \psi \right) = \hat{\mathbf{\Omega}}\cdot \mathrm{grad} \left( \psi \right)

El segundo término de la ecuación 2.43 queda entonces como la divergencia de la integral sobre \hat{\mathbf{\Omega}} del producto escalar entre la dirección \hat{\mathbf{\Omega}} por el flujo angular \psi

\begin{gathered} \frac{1}{v} \frac{\partial}{\partial t} \left[ \int \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}}\right] + \text{div} \left [ \int \left( \hat{\mathbf{\Omega}}\cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t)\right)\, d\hat{\mathbf{\Omega}}\right] \\ + \Sigma_t(\mathbf{x}, E) \cdot \left[ \int \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}}\right] = \int q(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} \end{gathered}

Recordando una vez más la definición 2.11 del flujo escalar \phi y definición 2.12 del vector corriente \mathbf{J},

\begin{aligned} \phi(\mathbf{x}, E, t) &= \int_{4\pi} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}}\\ \mathbf{J}(\mathbf{x},E,t) &= \int_{4\pi} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\right] \, d\hat{\mathbf{\Omega}} \end{aligned} y definiendo una fuente de neutrones escalar que incluya scattering, fisiones y/o fuentes independientes integrada sobre 4\pi

Q(\mathbf{x}, E, t) = \int_{4\pi} q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} + \int_{4\pi} q_f(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} + \int_{4\pi} s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} podemos escribir

\frac{1}{v} \frac{\partial}{\partial t} \Big[ \phi(\mathbf{x}, E, t) \Big] + \text{div} \Big[ \mathbf{J}(\mathbf{x}, E, t) \Big] + \Sigma_t(\mathbf{x}, E) \cdot \phi(\mathbf{x}, E, t) = Q(\mathbf{x}, E, t) \tag{2.44}

Observación. La ecuación 2.44 refleja la conservación del momento de orden cero del flujo angular \psi de neutrones con respecto a las direcciones \hat{\mathbf{\Omega}}, es decir la conservación de neutrones totales. Dado que proviene de integrar la ecuación de transporte sobre todas las direcciones posible, es tan exacta como la propia ecuación de transporte.

2.4.1.1 Producciones

El miembro derecho de la ecuación 2.44 representa las producciones de neutrones integradas sobre todas las direcciones y es igual a la integral de las tres contribuciones individuales debidas a scattering, fisión y fuentes independientes:

\begin{aligned} Q(\mathbf{x}, E, t) &= \int_{4\pi} q_s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} + \int_{4\pi} q_f(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} + \int_{4\pi} s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}}\\ &= Q_s(\mathbf{x}, E, t) + Q_f(\mathbf{x}, E, t) + S(\mathbf{x}, E, t) \end{aligned}

2.4.1.1.1 Fuente por scattering

Para evaluar la contribución debida al scattering de neutrones podemos integrar la ecuación 2.37 sobre todas las direcciones emergentes \hat{\mathbf{\Omega}}:

\begin{gathered} Q_s(\mathbf{x}, E, t) = \int_{4\pi} \Bigg\{ \frac{1}{4\pi} \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \phi(\mathbf{x}, E^{\prime}, t) \, dE^\prime \\ + \frac{3}{4\pi} \int_{0}^{\infty} \Sigma_{s_1}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \left(\mathbf{J}(\mathbf{x},E^{\prime},t) \cdot \hat{\mathbf{\Omega}}\right) \, dE^\prime \\ + \sum_{\ell=2}^\infty \int_{0}^{\infty} \left[ \Sigma_{s_\ell}(\mathbf{x}, E^{\prime} \rightarrow E) \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E^{\prime}, t) \cdot Y_\ell^{m}(\hat{\mathbf{\Omega}}) \right] \, dE^{\prime} \Bigg\} \, d\hat{\mathbf{\Omega}} \end{gathered}

Por la mismas razones que las esgrimidas al analizar la ecuación 2.34, solamente el primer término del integrando sobre \hat{\mathbf{\Omega}} resulta en una contribución diferente de cero. Luego la fuente de neutrones debido a scattering integrada en 4\pi se simplifica a

Q_s(\mathbf{x}, E, t) = \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \phi(\mathbf{x}, E^\prime, t) \, dE^\prime \tag{2.45}

2.4.1.1.2 Fuente por fisión

El término que representa la fuente por fisión es la integral sobre todas las posibles direcciones del término de fuentes de fisión q_f. Para el caso de la ecuación 2.40, tenemos

\begin{aligned} Q_f(\mathbf{x},E,t) &= \int_{4\pi} \left[ \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \phi(\mathbf{x}, E^\prime, t) \, dE^\prime \right] \, d\hat{\mathbf{\Omega}}\\ &= \chi(E) \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \phi(\mathbf{x}, E^\prime, t) \, dE^\prime \end{aligned} \tag{2.46}

2.4.1.1.3 Fuente independiente

La fuente independiente integrada es directamente la integral sobre \hat{\mathbf{\Omega}} de la fuente independiente angular s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t):

S(\mathbf{x},E,t) = \int_{4\pi} s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \, d\hat{\mathbf{\Omega}} = s_0(\mathbf{x},E,t) \tag{2.47} es decir, el momento de orden cero de la distribución angular de la fuente s.

2.4.2 Momento de orden uno

Comencemos esta sección recordando la ecuación 2.28, explicitando los términos de fuentes por scattering (ecuación 2.32), fisión (ecuación 2.26) y fuentes independientes:

\begin{gathered} \frac{1}{v} \frac{\partial}{\partial t} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] + \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] + \Sigma_t(\mathbf{x}, E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) = \\ \int_{0}^{\infty} \sum_{\ell=0}^\infty \left[ \Sigma_{s_\ell}(\mathbf{x}, E^{\prime} \rightarrow E) \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E^{\prime}, t) \cdot Y_\ell^{m}(\hat{\mathbf{\Omega}}) \right] \, dE^{\prime} \\ + \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \phi(\mathbf{x}, E^\prime, t) \, dE^\prime + s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \end{gathered} \tag{2.48}

Multipliquemos esta ecuación escalar por el versor \hat{\mathbf{\Omega}} e integremos sobre todas las posibles direcciones para obtener una ecuación vectorial de dimensión tres:

\begin{gathered} \underbrace{\int_{4\pi} \left( \frac{1}{v} \frac{\partial}{\partial t} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}}_\text{derivada temporal} + \underbrace{\int_{4\pi} \left( \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}}_\text{advección} \\ + \underbrace{\int_{4\pi} \left( \Sigma_t(\mathbf{x}, E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}}_\text{absorción total} = \\ \underbrace{\int_{4\pi} \left( \int_{0}^{\infty} \sum_{\ell=0}^\infty \left[ \Sigma_{s_\ell}(\mathbf{x}, E^{\prime} \rightarrow E) \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E^{\prime}, t) \cdot Y_\ell^{m}(\hat{\mathbf{\Omega}}) \right] \, dE^{\prime} \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}}_\text{scattering} \\ + \underbrace{\int_{4\pi} \left( \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \phi(\mathbf{x}, E^\prime, t) \, dE^\prime \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}}_\text{fisión} + \underbrace{\int_{4\pi} \left( s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}}_\text{fuentes independientes} \end{gathered} \tag{2.49}

Analicemos en las seis sub-secciones que siguen los términos de esta expresión un por uno, teniendo en cuenta los desarrollos matemáticos que hemos realizado a lo largo de todo el capítulo.

2.4.2.1 Derivada temporal

El primer término corresponde a la derivada temporal de la corriente. En efecto

\begin{aligned} \int_{4\pi} \left( \frac{1}{v} \frac{\partial}{\partial t} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}} & = \frac{1}{v(E)} \frac{\partial}{\partial t}\left[ \int_{4\pi} \left( \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}\right] \\ & = \sqrt{\frac{m}{2E}} \frac{\partial}{\partial t}\Big[ \mathbf{J}(\mathbf{x}, E, t) \Big] \end{aligned} \tag{2.50}

2.4.2.2 Advección

El término de advección parece el más sencillo pero de hecho es el más difícil de analizar. Es más, es tan complicado que es aquí donde necesitamos hacer la aproximación más importante de la formulación de difusión. Tenemos que suponer que los coeficientes \Psi_\ell^m de la expansión del flujo angular \psi en armónicos esféricos dado en la ecuación 2.33 son cero para \ell \geq 2, es decir

\psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \simeq \frac{1}{4\pi} \left[ \phi(\mathbf{x}, E, t) + 3 \cdot \left(\mathbf{J}(\mathbf{x}, E, t) \cdot \hat{\mathbf{\Omega}}\right) \right]

Con esta suposición, el término de advección queda aproximadamente igual a

\begin{gathered} \int_{4\pi} \left( \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}\simeq \\ \frac{1}{4\pi} \cdot \left\{ \int_{4\pi} \left( \hat{\mathbf{\Omega}}\cdot \text{grad}\left(\phi\right) \right) \cdot \hat{\mathbf{\Omega}}\, d\hat{\mathbf{\Omega}} + 3 \cdot \int_{4\pi} \left[ \hat{\mathbf{\Omega}}\cdot \text{grad}\left( \mathbf{J} \cdot \hat{\mathbf{\Omega}}\right) \right] \cdot \hat{\mathbf{\Omega}}\, d\hat{\mathbf{\Omega}}\right\} \end{gathered} \tag{2.51}

La integral sobre el gradiente flujo escalar \nabla \phi es

\begin{aligned} \int_{4\pi} \left[\hat{\mathbf{\Omega}}\cdot \text{grad}\left(\phi\right) \right] \cdot \hat{\mathbf{\Omega}}\, d\hat{\mathbf{\Omega}} &= \int_{4\pi} \left( \begin{bmatrix} \hat{\Omega}_x & \hat{\Omega}_y & \hat{\Omega}_z \end{bmatrix} \begin{bmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z} \end{bmatrix} \right) \cdot \begin{bmatrix} \hat{\Omega}_x \\ \hat{\Omega}_y \\ \hat{\Omega}_z \end{bmatrix} \, d\hat{\mathbf{\Omega}} \\ &= \int_{4\pi} \left( \hat{\Omega}_x \cdot \frac{\partial \phi}{\partial x} + \hat{\Omega}_y \cdot \frac{\partial \phi}{\partial y} + \hat{\Omega}_z \cdot \frac{\partial \phi}{\partial z} \right) \cdot \begin{bmatrix} \hat{\Omega}_x \\ \hat{\Omega}_y \\ \hat{\Omega}_z \end{bmatrix} \, d\hat{\mathbf{\Omega}} \\ &= \int_{4\pi} \begin{bmatrix} \hat{\Omega}_x \hat{\Omega}_x \cdot \frac{\partial \phi}{\partial x} + \hat{\Omega}_x \hat{\Omega}_y \cdot \frac{\partial \phi}{\partial y} + \hat{\Omega}_x \hat{\Omega}_z \cdot \frac{\partial \phi}{\partial z} \\ \hat{\Omega}_y \hat{\Omega}_x \cdot \frac{\partial \phi}{\partial x} + \hat{\Omega}_y \hat{\Omega}_y \cdot \frac{\partial \phi}{\partial y} + \hat{\Omega}_y \hat{\Omega}_z \cdot \frac{\partial \phi}{\partial z} \\ \hat{\Omega}_z \hat{\Omega}_x \cdot \frac{\partial \phi}{\partial x} + \hat{\Omega}_z \hat{\Omega}_y \cdot \frac{\partial \phi}{\partial y} + \hat{\Omega}_z \hat{\Omega}_z \cdot \frac{\partial \phi}{\partial z} \end{bmatrix} \, d\hat{\mathbf{\Omega}} \\ &= \left( \int_{4\pi} \begin{bmatrix} \hat{\Omega}_x^2 & \hat{\Omega}_x \hat{\Omega}_y & \hat{\Omega}_x \hat{\Omega}_z \\ \hat{\Omega}_y \hat{\Omega}_x & \hat{\Omega}_y^2 & \hat{\Omega}_y \hat{\Omega}_z \\ \hat{\Omega}_z \hat{\Omega}_x & \hat{\Omega}_z \hat{\Omega}_y & \hat{\Omega}_z^2 \end{bmatrix} \, d\hat{\mathbf{\Omega}} \right) \cdot \text{grad}\left[ \phi(\mathbf{x}, E, t) \right] \end{aligned}

Recordando el teorema 2.7, los elementos de la diagonal dan como resultado 4\pi/3 mientras que el resto se anulan:

\begin{aligned} \int_{4\pi} \left[\hat{\mathbf{\Omega}}\cdot \text{grad}\left(\phi\right) \right] \cdot \hat{\mathbf{\Omega}}\, d\hat{\mathbf{\Omega}} &= \frac{4\pi}{3} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z} \end{bmatrix} \\ &= \frac{4\pi}{3} \cdot \begin{bmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z} \end{bmatrix} = 4\pi \cdot \left[ \frac{1}{3} \cdot \text{grad}\left[ \phi(\mathbf{x}, E, t) \right] \right] \end{aligned}

Por otro lado, el segundo término de la ecuación 2.51 se anula. En efecto,

\int_{4\pi} \left[ \hat{\mathbf{\Omega}}\cdot \text{grad}\left( \mathbf{J} \cdot \hat{\mathbf{\Omega}}\right) \right] \cdot \hat{\mathbf{\Omega}}\, d\hat{\mathbf{\Omega}}

= \int_{4\pi} \left\{ \begin{bmatrix} \hat{\Omega}_x & \hat{\Omega}_y & \hat{\Omega}_z \end{bmatrix} \cdot \text{grad} \left( J_x \cdot \hat{\Omega}_x + J_y \cdot \hat{\Omega}_y + J_z \cdot \hat{\Omega}_z \right) \right\} \cdot \begin{bmatrix} \hat{\Omega}_x \\ \hat{\Omega}_y \\ \hat{\Omega}_z \end{bmatrix} \, d\hat{\mathbf{\Omega}}

= \int_{4\pi} \left\{ \begin{bmatrix} \hat{\Omega}_x & \hat{\Omega}_y & \hat{\Omega}_z \end{bmatrix} \cdot \begin{bmatrix} \frac{\partial J_x}{\partial x} \cdot \hat{\Omega}_x + \frac{\partial J_y}{\partial x} \cdot \hat{\Omega}_y + \frac{\partial J_z}{\partial x} \cdot \hat{\Omega}_z \\ \frac{\partial J_x}{\partial y} \cdot \hat{\Omega}_x + \frac{\partial J_y}{\partial y} \cdot \hat{\Omega}_y + \frac{\partial J_z}{\partial y} \cdot \hat{\Omega}_z \\ \frac{\partial J_x}{\partial z} \cdot \hat{\Omega}_x + \frac{\partial J_y}{\partial z} \cdot \hat{\Omega}_y + \frac{\partial J_z}{\partial z} \cdot \hat{\Omega}_z \end{bmatrix} \right\} \cdot \begin{bmatrix} \hat{\Omega}_x \\ \hat{\Omega}_y \\ \hat{\Omega}_z \end{bmatrix} \, d\hat{\mathbf{\Omega}}

\begin{aligned} = \int_{4\pi} \Bigg( & \frac{\partial J_x}{\partial x} \cdot \hat{\Omega}_x^2 + \frac{\partial J_y}{\partial x} \cdot \hat{\Omega}_y \hat{\Omega}_x + \frac{\partial J_z}{\partial x} \cdot \hat{\Omega}_z \hat{\Omega}_x + \\ & \frac{\partial J_x}{\partial y} \cdot \hat{\Omega}_x \hat{\Omega}_y + \frac{\partial J_y}{\partial y} \cdot \hat{\Omega}_y^2 + \frac{\partial J_z}{\partial y} \cdot \hat{\Omega}_z \hat{\Omega}_y + \\ & \frac{\partial J_x}{\partial z} \cdot \hat{\Omega}_x \hat{\Omega}_z + \frac{\partial J_y}{\partial z} \cdot \hat{\Omega}_y \hat{\Omega}_z + \frac{\partial J_z}{\partial z} \cdot \hat{\Omega}_z^2 \Bigg) \cdot \begin{bmatrix} \hat{\Omega}_x \\ \hat{\Omega}_y \\ \hat{\Omega}_z \end{bmatrix} \, d\hat{\mathbf{\Omega}} \end{aligned}

El integrando es un vector \mathbf{v} \in \mathbb{R}^3 cuyos tres elementos son

\begin{aligned} v_1 =& \frac{\partial J_x}{\partial x} \cdot \hat{\Omega}_x^3 + \frac{\partial J_y}{\partial x} \cdot \hat{\Omega}_y \hat{\Omega}_x^2 + \frac{\partial J_z}{\partial x} \cdot \hat{\Omega}_z \hat{\Omega}_x^2 + \\ & \frac{\partial J_x}{\partial y} \cdot \hat{\Omega}_x^2 \hat{\Omega}_y + \frac{\partial J_y}{\partial y} \cdot \hat{\Omega}_y^2 \hat{\Omega}_x + \frac{\partial J_z}{\partial y} \cdot \hat{\Omega}_z \hat{\Omega}_y \hat{\Omega}_x + \\ & \frac{\partial J_x}{\partial z} \cdot \hat{\Omega}_x^2 \hat{\Omega}_z + \frac{\partial J_y}{\partial z} \cdot \hat{\Omega}_y \hat{\Omega}_z \hat{\Omega}_x + \frac{\partial J_z}{\partial z} \cdot \hat{\Omega}_z^2 \hat{\Omega}_x \end{aligned}

\begin{aligned} v_2 =& \frac{\partial J_x}{\partial x} \cdot \hat{\Omega}_x^2 \hat{\Omega}_y + \frac{\partial J_y}{\partial x} \cdot \hat{\Omega}_y^2 \hat{\Omega}_x + \frac{\partial J_z}{\partial x} \cdot \hat{\Omega}_z \hat{\Omega}_x \hat{\Omega}_y + \\ & \frac{\partial J_x}{\partial y} \cdot \hat{\Omega}_x \hat{\Omega}_y^2 + \frac{\partial J_y}{\partial y} \cdot \hat{\Omega}_y^3 + \frac{\partial J_z}{\partial y} \cdot \hat{\Omega}_z \hat{\Omega}_y^2 + \\ & \frac{\partial J_x}{\partial z} \cdot \hat{\Omega}_x \hat{\Omega}_z \hat{\Omega}_y + \frac{\partial J_y}{\partial z} \cdot \hat{\Omega}_y^2 \hat{\Omega}_z + \frac{\partial J_z}{\partial z} \cdot \hat{\Omega}_z^2 \hat{\Omega}_y \end{aligned}

y

\begin{aligned} v_3 =& \frac{\partial J_x}{\partial x} \cdot \hat{\Omega}_x^2 \hat{\Omega}_z + \frac{\partial J_y}{\partial x} \cdot \hat{\Omega}_y \hat{\Omega}_x \hat{\Omega}_z + \frac{\partial J_z}{\partial x} \cdot \hat{\Omega}_z^2 \hat{\Omega}_x + \\ & \frac{\partial J_x}{\partial y} \cdot \hat{\Omega}_x \hat{\Omega}_y \hat{\Omega}_z + \frac{\partial J_y}{\partial y} \cdot \hat{\Omega}_y^2 \hat{\Omega}_z + \frac{\partial J_z}{\partial y} \cdot \hat{\Omega}_z^2 \hat{\Omega}_y + \\ & \frac{\partial J_x}{\partial z} \cdot \hat{\Omega}_x \hat{\Omega}_z^2 + \frac{\partial J_y}{\partial z} \cdot \hat{\Omega}_y \hat{\Omega}_z^2 + \frac{\partial J_z}{\partial z} \cdot \hat{\Omega}_z^3 \end{aligned}

Los veintisiete términos tienen al menos un coseno dirección elevado a un potencia impar, por lo que por el teorema 2.8 su integral sobre 4\pi es igual a cero. Entonces, podemos aproximar el término de advección bajo la suposición de que el flujo angular es linealmente anisótropo como

\int_{4\pi} \left( \hat{\mathbf{\Omega}}\cdot \text{grad} \left[ \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \right] \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}\simeq \frac{1}{3} \cdot \text{grad} \left[ \phi(\mathbf{x}, E,t ) \right] \tag{2.52}

Observación. La referencia [1, p. 88] indica

If one keeps the higher terms in the Legendre polynomial expansion of \psi, there then results, as can be shown by an easy calculation, the exact expression

J = - \frac{1}{3 \left( \Sigma_{tr} + \Sigma_a \right)} \frac{d}{dx} \left[ \phi(x) \left(1 + 2 \frac{\psi_2(x)}{\phi(x)} \right) \right]

2.4.2.3 Absorción total

El siguiente es el término de absorciones totales escrito en forma vectorial con respecto a la corriente

\begin{aligned} \int_{4\pi} \left( \Sigma_t(\mathbf{x}, E) \cdot \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}} & = \Sigma_t(\mathbf{x}, E) \cdot \int_{4\pi} \left( \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}\\ & = \Sigma_t(\mathbf{x}, E) \cdot \mathbf{J}(\mathbf{x}, E, t) \end{aligned} \tag{2.53}

2.4.2.4 Scattering

El término de scattering parece complicado, pero en realidad ya lo hemos resuelto al derivar la ecuación ecuación 2.35. En primer lugar, partamos de la ecuación ecuación 2.37 multiplicada por \hat{\mathbf{\Omega}} e integrada en 4\pi:

\begin{gathered} \int_{4\pi} \left[ \frac{1}{4\pi} \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \phi(\mathbf{x}, E^{\prime}, t) \cdot \hat{\mathbf{\Omega}}\, dE^\prime \right] \, d\hat{\mathbf{\Omega}}\\ + \int_{4\pi} \left[ \frac{3}{4\pi} \int_{0}^{\infty} \Sigma_{s_1}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \left(\mathbf{J}(\mathbf{x},E^{\prime},t) \cdot \hat{\mathbf{\Omega}}\right) \cdot \hat{\mathbf{\Omega}}\, dE^\prime \right] \, d\hat{\mathbf{\Omega}}\\ + \int_{4\pi} \left\{ \sum_{\ell=2}^\infty \int_{0}^{\infty} \left[ \Sigma_{s_\ell}(\mathbf{x}, E^{\prime} \rightarrow E) \sum_{m=-\ell}^{+\ell} \Psi_\ell^m (\mathbf{x}, E^{\prime}, t) \cdot Y_\ell^{m}(\hat{\mathbf{\Omega}}) \cdot \hat{\mathbf{\Omega}}\right] \, dE^{\prime} \right\} \, d\hat{\mathbf{\Omega}} \end{gathered}

En forma similar al argumento planteado en la ecuación 2.34, el primer término se anula. Los términos de la sumatoria para \ell \geq 2 también se anulan por la propiedad de ortogonalidad de los armónicos esféricos (teorema 2.4) y la ecuación 2.36 que indica que \hat{\mathbf{\Omega}} es proporcional a Y_1^m(\hat{\mathbf{\Omega}}). Entonces el término de scattering queda

\begin{aligned} &= \frac{3}{4\pi} \int_{4\pi} \left\{ \int_0^\infty \Sigma_{s_1}(\mathbf{x},E^\prime \rightarrow E) \cdot \left( J_x \hat{\Omega}_x + J_y \hat{\Omega}_y + J_z \hat{\Omega}_z \right) \cdot \begin{bmatrix} \hat{\Omega}_x \\ \hat{\Omega}_y \\ \hat{\Omega}_z \end{bmatrix} \, dE^\prime \right\} \, d\hat{\mathbf{\Omega}}\\ &= \frac{3}{4\pi} \int_{4\pi} \left\{ \int_0^\infty \Sigma_{s_1}(\mathbf{x},E^\prime \rightarrow E) \cdot \begin{bmatrix} J_x \hat{\Omega}_x \hat{\Omega}_x + J_y \hat{\Omega}_y \hat{\Omega}_x + J_z \hat{\Omega}_z \hat{\Omega}_x \\ J_x \hat{\Omega}_x \hat{\Omega}_y + J_y \hat{\Omega}_y \hat{\Omega}_y + J_z \hat{\Omega}_z \hat{\Omega}_y \\ J_x \hat{\Omega}_x \hat{\Omega}_z + J_y \hat{\Omega}_y \hat{\Omega}_z + J_z \hat{\Omega}_z \hat{\Omega}_z \end{bmatrix} \, dE^\prime \right\} \, d\hat{\mathbf{\Omega}} \end{aligned}

Teniendo además en cuenta el teorema 2.7, el término de scattering toma la inocua forma de

\int_0^\infty \Sigma_{s_1}(\mathbf{x},E^\prime \rightarrow E) \cdot \mathbf{J}(\mathbf{x}, E^\prime,t) \, dE^\prime \tag{2.54}

2.4.2.5 Fisiones

El siguiente es el término de fisiones, cuya integral se anula. En efecto,

\int_{4\pi} \left( \frac{\chi(E)}{4\pi} \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \phi(\mathbf{x}, E^\prime, t) \, dE^\prime \cdot \hat{\mathbf{\Omega}}\right) \, d\hat{\mathbf{\Omega}}= 0 \tag{2.55} ya que el integrando es el producto de una factor que no depende del ángulo por el versor {\hat{\mathbf{\Omega}}}. En forma equivalente, estamos evaluando el momento de orden \ell=1 de una fuente de fisión. Dado que ésta es isótrópa, el único momento diferente de cero es el de orden \ell=0.

2.4.2.6 Fuentes independientes

El término de fuentes independientes es igual a un vector cuyas componentes son los tres coeficientes correspondientes a \ell=1 en la expansión en armónicos esféricos sobre el ángulo \hat{\mathbf{\Omega}} de la fuente s:

\begin{aligned} \int_{4\pi} s(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \cdot \hat{\mathbf{\Omega}}\, d\hat{\mathbf{\Omega}} & = \sqrt{\frac{3}{4\pi}} \cdot \begin{bmatrix} s_1^{+1}(\mathbf{x},E,t) \\ s_1^{-1}(\mathbf{x},E,t) \\ s_1^{0}(\mathbf{x},E,t) \\ \end{bmatrix} \\ & = \sqrt{\frac{3}{4\pi}} \cdot \mathbf{s}_1(\mathbf{x},E,t) \end{aligned} \tag{2.56}

Si las fuentes independientes son isotrópicas en el marco de referencia del reactor, los tres coeficientes son cero y la integral es nula.

2.4.3 Ley de Fick

Estamos entonces en condiciones de volver a reunir los seis términos de la ecuación 2.49 que analizamos por separado en las ecuaciones

• 2.50 (derivada temporal),
• 2.52 (advección),
• 2.53 (absorciones totales),
• 2.54 (scattering),
• 2.55 (fisiones), y
• 2.56 (fuentes)

y concluir que al multiplicar la ecuación 2.48 por \hat{\mathbf{\Omega}} e integrar en todas las posibles direcciones, obtenemos

\begin{gathered} \frac{1}{v(E)} \frac{\partial \mathbf{J}}{\partial t} + \frac{1}{3} \cdot \text{grad} \big[ \phi(\mathbf{x}, E,t ) \big] + \Sigma_t(\mathbf{x}, E) \cdot \mathbf{J}(\mathbf{x}, E, t) = \\ \int_0^\infty \Sigma_{s_1}(\mathbf{x},E^\prime \rightarrow E) \cdot \mathbf{J}(\mathbf{x}, E^\prime,t) \, dE^\prime + \sqrt{\frac{3}{4\pi}} \cdot \mathbf{s}_1(\mathbf{x},E,t) \end{gathered} \tag{2.57}

Para arribar finalmente a la ecuación de difusión necesitamos tres nuevas suposiciones:

1. Que

   1. el problema sea estacionario, o

   2. que

   \frac{3}{v} \frac{\partial \mathbf{J}}{\partial t} \ll \text{grad} \left[ \phi(\mathbf{x}, E,t ) \right]

2. Que

   1. no haya fuentes independientes, o

   2. que la fuente independiente sea isótropa de forma tal que los tres coeficientes s_\ell^m de la ecuación 2.55 sean iguales a cero.

3. Que

   1. el scattering sea isótropo (en el marco de referencia del reactor), o

   2. que

      \int_0^\infty \Sigma_{s_1}(\mathbf{x}, E^\prime \rightarrow E) \cdot \mathbf{J}(\mathbf{x}, E^\prime, t) \, dE^\prime \simeq \int_0^\infty \Sigma_{s_1}(\mathbf{x}, E \rightarrow E^\prime) \cdot \mathbf{J}(\mathbf{x}, E, t) \, dE^\prime \tag{2.58}

      El miembro izquierdo representa el in-scattering de neutrones de todas las energías mientras que el miembro derecho es el out-scattering de neutrones de energía E hacia todas las otras energías E^\prime. Si la absorción es pequeña, estas dos expresiones se deberían balancear aproximadamente.

Si al menos una de las dos condiciones a ó b de cada una de las tres suposiciones i, ii y iii son ciertas (o razonables), entonces volviendo a la ecuación 2.57, tenemos

\begin{aligned} \frac{1}{3} \cdot \text{grad} \left[ \phi(\mathbf{x}, E,t ) \right] + \Sigma_t(\mathbf{x}, E) \cdot \mathbf{J}(\mathbf{x}, E, t) & \simeq \int_0^\infty \Sigma_{s_1}(\mathbf{x}, E \rightarrow E^\prime) \cdot \mathbf{J}(\mathbf{x}, E, t) \, dE^\prime \\ & \simeq \int_0^\infty \Sigma_{s_1}(\mathbf{x}, E \rightarrow E^\prime) \, dE^\prime \cdot \mathbf{J}(\mathbf{x}, E, t) \\ & \simeq \mu_0(\mathbf{x}, E) \int_0^\infty \Sigma_{s_0}(\mathbf{x}, E \rightarrow E^\prime) \, dE^\prime \cdot \mathbf{J}(\mathbf{x}, E, t) \\ & \simeq \mu_0(\mathbf{x}, E) \cdot \Sigma_{s_t}(\mathbf{x}, E) \cdot \mathbf{J}(\mathbf{x}, E, t) \end{aligned} donde en los últimos dos pasos hemos utilizado la definición 2.7 y la sección eficaz total de scattering \Sigma_s(\mathbf{x}, E) de la ecuación 2.2 evaluada en función del coeficiente \Sigma_{s_0} según la ecuación 2.5. Con esta expresión podemos relacionar el vector corriente \mathbf{J} con el gradiente del flujo escalar \phi como

\mathbf{J}(\mathbf{x}, E, t) = -\frac{1}{3 \left[ \Sigma_t(\mathbf{x}, E) - \mu_0(\mathbf{x}, E) \cdot \Sigma_{s_t}(\mathbf{x},E) \right] } \cdot \text{grad} \left[ \phi(\mathbf{x}, E,t ) \right]

Definición 2.17 El coeficiente de difusión D definido como

D(\mathbf{x}, E) = \frac{1}{3 \left[ \Sigma_t(\mathbf{x}, E) - \mu_0(\mathbf{x}, E) \cdot \Sigma_{s_t}(\mathbf{x},E) \right]} \tag{2.59} es tal que, si

1. el flujo angular es linealmente anisótropo \psi \simeq (\phi + 3\mathbf{J})/4\pi
2. el problema es estacionario o 3/v \cdot \partial \mathbf{J}/\partial t \ll \nabla \phi
3. no hay fuentes independientes o éstas son isotrópicas
4. el scattering es isótropo o el in-scattering es similar al out-scattering \int \Sigma_{s_1}(E^\prime \rightarrow E) \cdot \mathbf{J}(E^\prime) \, dE^\prime \simeq \int \Sigma_{s_1}(E \rightarrow E^\prime) \cdot \mathbf{J}(E) \, dE^\prime

entonces se cumple la Ley de Fick

\mathbf{J}(\mathbf{x}, E, t) \simeq - D(\mathbf{x}, E) \cdot \text{grad} \left[ \phi(\mathbf{x}, E, t) \right] \tag{2.60} según la cual el vector corriente \mathbf{J} es proporcional a menos el gradiente del flujo escalar \phi a través de un coeficiente de difusión D dado por la ecuación 2.59.

Observación. La ley de Fick refleja, en forma aproximada, la conservación del momento de orden uno del flujo angular \psi con respecto a todas las direcciones de vuelo \hat{\mathbf{\Omega}}.

Observación. Dado que las secciones eficaces macroscópicas tienen unidades de inversa de longitud (definición 2.1), el coeficiente de difusión D tiene unidades de longitud.

2.4.4 La ecuación de difusión

Podemos combinar los dos resultados de la conservación de momentos de orden cero y uno desarrollados en las secciones anteriores teniendo en cuenta las expresiones dadas por las ecuaciones

• 2.44 (conservación),
• 2.45 (scattering),
• 2.46 (fisión),
• 2.47 (fuentes), y
• 2.60 (ley de Fick)

para obtener finalmente la celebrada ecuación de difusión de neutrones

\begin{gathered} \sqrt{\frac{m}{2E}} \frac{\partial}{\partial t} \Big[ \phi(\mathbf{x}, E, t) \Big] - \text{div} \Big[ D(\mathbf{x}, E) \cdot \text{grad} \left[ \phi(\mathbf{x}, E, t) \right] \Big] + \Sigma_t(\mathbf{x}, E) \cdot \phi(\mathbf{x}, E, t) = \\ \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \phi(\mathbf{x}, E^\prime, t) \, dE^\prime + \chi(E) \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \phi(\mathbf{x}, E^\prime, t) \, dE^\prime + s_0(\mathbf{x}, E, t) \end{gathered} \tag{2.61} que es una ecuación integro-diferencial elíptica en derivadas parciales de segundo orden sobre el espacio (los operadores divergencia y gradiente operan sólo sobre las coordenadas espaciales), y de primer orden sobre el tiempo para la incógnita \phi definida sobre

1. el espacio \mathbf{x},
2. la energía E, y
3. el tiempo t.

Observación. La incógnita de la ecuación de difusión es el flujo escalar \phi que no depende de \hat{\mathbf{\Omega}}.

Los datos de entrada para la ecuación de difusión de neutrones son:

• Las secciones eficaces \Sigma_t y \nu\Sigma_f como función del espacio \mathbf{x} y de la energía E.
• El espectro de fisión \chi en función de la energía E.
• El coeficiente de difusión D como función del espacio \mathbf{x} y de la energía E.
• La fuente independiente de neutrones s, que debe ser isótropa.
• El parámetro constante m, que es la masa en reposo del neutrón.

Observación. En estado estacionario, la ecuación de difusión de neutrones es

\begin{gathered} - \text{div} \Big[ D(\mathbf{x}, E) \cdot \text{grad} \left[ \phi(\mathbf{x}, E) \right] \Big] + \Sigma_t(\mathbf{x}, E) \cdot \phi(\mathbf{x}, E) = \\ \int_{0}^{\infty} \Sigma_{s_0}(\mathbf{x}, E^{\prime} \rightarrow E) \cdot \phi(\mathbf{x}, E^\prime) \, dE^\prime + \chi(E) \int_{0}^{\infty} \nu\Sigma_f(\mathbf{x}, E^\prime) \cdot \phi(\mathbf{x}, E^\prime) \, dE^\prime + s_0(\mathbf{x}, E) \end{gathered} \tag{2.62}

2.4.5 Condiciones de contorno

La ecuación de difusión es elíptica sobre las coordenadas espaciales por lo que debemos especificar, además de las condiciones iniciales apropiadas en el caso transitorio, condiciones de contorno en toda la frontera \partial U del dominio espacial. Para el caso de una ecuación elíptica, éstas pueden ser de tipo

1. Dirichlet donde especificamos el valor del flujo escalar \phi en \Gamma_D \subset \partial U; o
2. Neumann donde fijamos el valor de la derivada normal \partial \phi/\partial n en \Gamma_N \subset \partial U; o
3. Robin donde damos una combinación lineal del flujo y de la derivada normal en \Gamma_R \subset \partial U.

Observación. Debe cumplirse que \Gamma_D \cap \Gamma_N \cap \Gamma_R = \emptyset y que \Gamma_D \cup \Gamma_N \cup \Gamma_R = \partial U.

Dada una superficie diferencial dA cuya normal exterior es \hat{\mathbf{n}}, la tasa de neutrones entrante por unidad de área a través de dicha superficie dA está dada por la ecuación 2.19 de la definición 2.12:

\tag{\ref{eq-jnegativa}} \ J_n^-(\mathbf{x},E,t) = \int_{\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} < 0} \psi(\mathbf{x}, \hat{\mathbf{\Omega}}, E, t) \left(\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}}\right) d\hat{\mathbf{\Omega}}

Despreciando los términos para \ell \geq 2 de la expansión de la ecuación 2.33 podemos estimar esta corriente como

\begin{aligned} J_n^-(\mathbf{x},E,t) & \simeq \int_{\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} < 0} \frac{1}{4\pi} \left [ \phi(\mathbf{x}, E, t) + 3 \, \mathbf{J}(\mathbf{x}, E, t) \cdot \hat{\mathbf{\Omega}}\right] \cdot \left(\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}}\right) d\hat{\mathbf{\Omega}} \\ & \simeq \frac{1}{4\pi} \phi(\mathbf{x}, E, t) \int_{0}^{-1} \mu^\prime \cdot 2\pi\, d\mu^\prime + \frac{3}{4\pi} \int_{\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}} < 0} \Big[ \mathbf{J}(\mathbf{x}, E, t) \cdot \hat{\mathbf{\Omega}}\Big] \cdot \left(\hat{\mathbf{\Omega}}\cdot \hat{\mathbf{n}}\right) d\hat{\mathbf{\Omega}}\\ & \simeq \frac{1}{4\pi} \phi(\mathbf{x}, E, t) \cdot 2\pi \cdot \frac{1}{2} + \frac{3}{4\pi} \cdot \Big[ \mathbf{J}(\mathbf{x}, E, t) \cdot \hat{\mathbf{n}} \Big] \cdot \left(- \frac{2}{3} \pi \right) \\ & \simeq \frac{1}{4} \phi(\mathbf{x}, E, t) - \frac{1}{2} \Big[ \mathbf{J}(\mathbf{x}, E, t) \cdot \hat{\mathbf{n}} \Big] \end{aligned} donde hemos usado el teorema 2.7 sobre una semi-esfera unitaria para resolver la segunda integral del miembro derecho. A la luz de la ley de Fick dada por la definición 2.17, podemos escribir

\begin{aligned} J_n^-(\mathbf{x},E,t) & \simeq \frac{1}{4} \cdot \phi(\mathbf{x}, E, t) + \frac{1}{2} \cdot D(\mathbf{x}, E) \cdot \left\{ \text{grad} \big[ \phi(\mathbf{x}, E, t)\big] \cdot \hat{\mathbf{n}} \right\} \\ & \simeq \frac{\phi(\mathbf{x}, E, t)}{4} + \frac{D(\mathbf{x}, E)}{2} \cdot \frac{\partial \phi}{\partial n} \end{aligned} lo que nos da una expresión para definir la condición de contorno de vacío para la ecuación de difusión.

Definición 2.18 En forma análoga a la definición 2.14, llamamos condición de contorno de vacío a la situación en la cual la corriente entrante a través de una porción de la frontera \partial U es cero, con lo que se debe cumplir:

\phi(\mathbf{x}, E, t) + 2 \cdot D(\mathbf{x}, E) \cdot \frac{\partial \phi}{\partial n} = 0 \quad\quad \forall \mathbf{x} \in \Gamma_V \subset \partial U

Observación. La definición 2.18 es aplicable solamente a la ecuación de difusión. No aplica a la ecuación de transporte.

Definimos el conjunto \Gamma_V \subset \partial U como el lugar geométrico de todos los puntos \mathbf{x} \in \partial U donde imponemos esta condición de contorno. Esta condición es de tipo Robin ya que se da el valor de una combinación lineal de la incógnita \phi y de su derivada normal \partial \phi/\partial n.

Definición 2.19 En forma análoga a la definición 2.15, llamamos condición de contorno de reflexión o de simetría cuando la corriente neta entrante en el punto \mathbf{x} \in \partial U es igual a cero. En este caso, por la ley de Fick debe anularse la derivada normal del flujo escalar evaluada en \mathbf{x}:

\text{grad} \big[ \phi(\mathbf{x}, E, t)\big] \cdot \hat{\mathbf{n}} = \frac{\partial \phi}{\partial n} = 0 \quad\quad \forall \mathbf{x} \in \Gamma_M \subset \partial U

Esta es una condición de tipo Neumann homogénea. Definimos el conjunto \Gamma_M \subset U como el lugar geométrico de todos los puntos \mathbf{x} \in \partial U donde imponemos esta condición de contorno.

Para el problema de difusión, a veces se suele utilizar una tercera condición de contorno basada en la idea que sigue. Si extrapolamos linealmente el flujo escalar \phi una distancia \zeta (que depende de la posición \mathbf{x} y de la energía E) en la dirección de la normal externa \hat{\mathbf{n}} en la frontera \partial U mediante una expansión de Taylor a primer orden, tenemos

\phi \big(\mathbf{x} + \zeta(\mathbf{x}, E) \cdot \hat{\mathbf{n}}, E, t \big) \Big|_{\mathbf{x} \in \partial U} \approx \phi(\mathbf{x}, E, t) + \frac{\partial \phi}{\partial n} \cdot \zeta(\mathbf{x}, E)

Si se cumple la condición de contorno de vacío dada por la definición 2.18

\phi(\mathbf{x}, E, t) + 2 \cdot D(\mathbf{x}, E) \cdot \frac{\partial \phi}{\partial n} = 0 entonces el flujo escalar extrapolado se anula en el punto

\mathbf{x}^* = \mathbf{x} + 2 \cdot D(\mathbf{x}, E) \cdot \hat{\mathbf{n}} como ilustramos en la figura 2.10.

Figura 2.10: El flujo escalar \phi(\mathbf{x}, E,t) extrapolado linealmente se anula a una distancia \zeta(\mathbf{x},E)= 2D(\mathbf{x},E) en una condición de contorno tipo vacío de la ecuación de difusión.

Si el valor numérico del coeficiente de difusión D(\mathbf{x}, E) (que tiene unidades de longitud) es mucho menor que el tamaño característico del dominio U entonces podemos aproximar \zeta \approx 0.

Definición 2.20 Llamamos condición de contorno de flujo nulo cuando el flujo escalar \phi se anula un punto \mathbf{x} \in \partial U:

\phi(\mathbf{x}, E, t) = 0 \quad\quad \forall \mathbf{x} \in \Gamma_N \subset \partial U

Definimos el conjunto \Gamma_N \subset \partial U como el lugar geométrico de todos los puntos \mathbf{x} \in \partial U donde imponemos esta condición de contorno. Matemáticamente esta condición es de tipo Dirichlet homogénea.

2.5 Esquema de solución multi-escala

La ecuación de transporte ecuación 2.29 describe completamente la interacción de neutrones con la materia y es exacta mientras

1. la población neutrónica sea lo suficientemente grande como para que podamos asumir que el flujo angular \psi es determinista, y
2. se cumplan las siete suposiciones listadas al comienzo del capítulo.

Los coeficientes tanto de la ecuación de transporte como de la ecuación de difusión son las secciones eficaces macroscópicas de los materiales presentes en el dominio U, que en principio son el producto de la sección eficaz microscópica por la densidad volumétrica de cada uno de los isótopos que componen dichos materiales.

Un neutrón nacido por fisión tiene una energía de aproximadamente 2 MeV, y cuando llega al equilibrio térmico con el medio puede alcanzar una energía de 0.02 eV. Esto es, la variable independiente E usualmente abarca ocho órdenes de magnitud. Recordando la figura 2.3, las secciones eficaces microscópicas pueden cambiar cinco o incluso seis órdenes de magnitud en este rango de energías, abarcando resonancias extremadamente difíciles de modelar matemáticamente.

Estas variaciones hace que sea prácticamente imposible resolver directamente la ecuación de transporte para obtener la dependencia del flujo angular \psi con el espacio, la dirección, la energía y eventualmente el tiempo sobre el dominio U a partir de las secciones eficaces microscópicas y de las concentraciones volumétricas de los isótopos. En la práctica se recurre a un esquema multi-escala, donde primero se evalúan y procesan las secciones eficaces microscópicas experimentales. Luego se evalúan celdas típicas de los componentes de los reactores nucleares (elementos combustibles, barras de control, etc.) para obtener secciones eficaces condensadas que finalmente son los coeficientes de la ecuación de transporte (o difusión) utilizada para realizar un cálculo a nivel de núcleo.¹²

2.5.1 Evaluación y procesamiento de secciones eficaces

Este nivel de cálculo es el punto central del trabajo de doctorado de la referencia [10]. A partir de mediciones experimentales, los datos se procesan de forma tal de que puedan ser evaluados y utilizados como bibliotecas de secciones eficaces microscópicas con las cuales realizar cálculos a nivel de celda.

2.5.2 Cálculo a nivel celda

Este nivel de cálculo es el punto central del trabajo de doctorado de la referencia [7]. A partir de bibliotecas de secciones eficaces microscópicas se procede a realizar cálculos de transporte de forma tal de calcular secciones eficaces macroscópicas a pocos grupos de energía que puedan ser usadas como los coeficientes de las ecuaciones de transporte utilizadas en el cálculo a nivel de núcleo.

2.5.3 Cálculo a nivel núcleo

Este nivel de cálculo es el punto central de esta tesis, especialmente en los capítulos 3 y 5. Las secciones eficaces macroscópicas que son los coeficientes de las ecuaciones de ordenadas discretas y difusión de neutrones multigrupo se suponen funciones conocidas del espacio.

[1]

Beckurts KH, Wirtz K, Neutron Physics. Springer-Verlag, 1964.

[2]

Brandt A, «Multi-Level Adaptive Solutions to Boundary-Value Problems», Mathematics of Computation, vol. 31, n.º 138, p. 333.390, abr. 1977.

[3]

Duderstadt JJ, Hamilton LJ, Nuclear Reactor Analysis. Wiley, New York, 1976.

[4]

Glasstone G S. Bell, Nuclear Reactor Theory. Krieger Publishing Company, 1970.

[5]

Henry AF, Nuclear Reactor Analysis. Cambridge, MIT, 1975.

[6]

Lamarsh JR, Introduction to Nuclear Reactor Theory. Addisson-Wesley, 1966.

[7]

Lestani H, «Metodología de análisis neutrónico de celdas de reactores de agua pesada», Tesis de Doctorado en Ingeniería Nuclear, Instituto Balseiro, 2014.

[8]

Lewis EE, Miller WF, Computational Methods of Neutron Transport. John Wiley; Sons, 1984.

[9]

Márquez Damián JI, «Multilevel Acceleration of Neutron Transport Calculations», mathesis, Georgia Institute of Technology, 2007.

[10]

Márquez Damián JI, «Desarrollo y aplicaciones de nuevas bibliotecas de secciones eficaces neutrónicas para H_2O, D_2O y HDO», Tesis de Doctorado en Ciencias de la Ingeniería, Instituto Balseiro, 2014.

[11]

Stammler RJG, Abbate MJ, Methods of Steady-State Reactor Physics in Nuclear Design. Academic Press, 1983.

[12]

Theler G, «Difusión de neutrones en mallas no estructuradas: comparación entre volúmenes y elementos finitos». Monografía Final de la materia «Introducción al método de elementos finitos», Universidad de Buenos Aires, 2013.

[13]

Theler G, Gómez Omil JP, Pellegrino E, «A shared-memory-based coupling scheme for modeling the behavior of a Nuclear Power Plant core», Mecánica Computacional, vol. XXXII, n.º Number 18 Multiphysics, pp. 1501-1517, 2013.

[14]

Theler G, Schivo M, «Estimación del coeficiente de reactividad por temperatura del combustible en reactores tipo Atucha mediante ajuste de modelos matematicos a mediciones experimentales», en Actas de la XL Reunión Anual de la Asociación Argentina de Tecnología Nuclear, Buenos Aires, 2013.

[15]

Theler G, Schivo M, Salom G, «Estimación del coeficiente de reactividad por temperatura del combustible de la Central Nuclear Atucha II a partir de mediciones de flujo neutrónico», en Actas de la XLI Reunión Anual de la Asociación Argentina de Tecnología Nuclear, Buenos Aires, 2014.

---

1. Pun intended.

2. Llegado el caso veremos cómo reducir el problema para casos particulares de dominios de una y dos dimensiones.

3. En inglés es cross section.

4. Se dice que durante las primeras mediciones experimentales de secciones eficaces los físicos americanos esperaban encontrar resultados del orden de las áreas transversales asociadas a los tamaños geométricos de los núcleos. Pero encontraron valores mucho más grandes, por lo que decían a modo de broma “this cross section is as big as a barn.”

5. Como ya hemos dicho, el término español “dispersión” como traducción del concepto de “scattering” no es muy feliz. A partir este punto, durante el resto de esta tesis usamos solamente la palabra scattering para referirnos a este concepto.

6. El coeficiente (2\ell+1)/2 aparece para que las expresiones que siguen sean consistentes con los usos y costumbres históricos de la evaluación de secciones eficaces (Sección 2.5.1) y de códigos de celda (Sección 2.5.2). En particular, aparece para que en la ecuación 2.5 ambos miembros tengan coeficientes unitarios. Es posible dar otras definiciones y desarrollar consistentemente la matemática para llegar a expresiones finales igualmente válidas, pero ello modificaría la definición de los coeficientes de la expansión dados por el corolario 2.1 y haría que las secciones eficaces calculadas a nivel de celda no puedan ser introducidas directamente en la entrada del código de núcleo que describimos en el capítulo 4. En particular, arribar a la ecuación 2.8 es de interés para la consistencia de las secciones eficaces entre códigos de diferente nivel. La referencia [8] utiliza otra forma de expandir el kernel de scattering que resulta en un factor dos de diferencia con respecto a la ecuación 2.4.

7. Como ya dijimos, esta nomenclatura es puramente académica. Una expresión más apropiada según la potencial aplicación industrial de los conceptos desarrollados en esta tesis sería “marco de referencia de la central nuclear”.

8. En el sentido del inglés prompt.

9. Si bien la dirección \hat{\mathbf{\Omega}}= [ \Omega_x \, \Omega_y \, \Omega_z]^T tiene tres componentes llamados cosenos dirección, sólo dos son independientes (por ejemplo las coordenadas angulares cenital \theta y azimutal \varphi) ya que debe cumplirse que \Omega_x^2 + \Omega_y^2 + \Omega_z^2 = 1.

10. Como ya hemos mencionado, no tenemos en cuenta el principio de Heisenberg.

11. Del inglés spanned.

12. En el sentido del inglés core.