4 Implementación computacional
C++ is a horrible language. It’s made more horrible by the fact that a lot of substandard programmers use it, to the point where it’s much much easier to generate total and utter crap with it. Quite frankly, even if the choice of C were to do nothing but keep the C++ programmers out, that in itself would be a huge reason to use C.
[…]
C++ leads to really really bad design choices. You invariably start using the “nice” library features of the language like STL and Boost and other total and utter crap, that may “help” you program, but causes:
infinite amounts of pain when they don’t work […]
inefficient abstracted programming models where two years down the road you notice that some abstraction wasn’t very efficient, but now all your code depends on all the nice object models around it, and you cannot fix it without rewriting your app.
[…]
So I’m sorry, but for something like git, where efficiency was a primary objective, the “advantages” of C++ is just a huge mistake. The fact that we also piss off people who cannot see that is just a big additional advantage.
Linus Torvalds, explaining why Git is written in C, 2007
C++ is a badly designed and ugly language.
It would be a shame to use it in Emacs.Richard M. Stallmann, explaining why Emacs is written in C, 2010
Hay virtualmente infinitas maneras \aleph_0 de diseñar un programa para que una computadora realice una determinada tarea. Y otras infinitas maneras \aleph_1 de implementarlas. La herramienta computacional desarrollada en esta tesis, denominada FeenoX [26] (ver Apéndice E para una explicación del nombre), fue diseñada siguiendo un patrón frecuente en la industria de software:
- el “cliente” define un documento denominado Sofware Requirements Specification, y
- el “proveedor” indica cómo cumplirá esos requerimientos en un Sofware Design Specification.
Una vez que ambas partes están de acuerdo, se comienza con el proyecto de ingeniería en sí con kick-off meetings, certificaciones de avance, órdenes de cambio, etc.
Como ya hemos mencionado, el SRS para FeenoX (apéndice A) es ficticio pero plausible. Podríamos pensarlo como un llamado a licitación por parte de una empresa, entidad pública o laboratorio nacional, para que un contratista desarrolle una herramienta computacional que permita resolver problemas matemáticos con interés práctico en aplicaciones de ingeniería. En forma muy resumida, el pliego requiere
buenas prácticas generales de desarrollo de software tales como
- trazabilidad del código fuente
- integración continua
- posibilidad de reportar errores
- portabilidad razonable
- disponibilidad de dependencias adecuadas
- documentación apropiada
que la herramienta pueda ser ejecutada en la nube
- a través de ejecución remota
- que provea mecanismos de reporte de estado
- con posibilidad de paralelización en diferentes nodos computacionales
que sea aplicable a problemas de ingeniería proveyendo
- eficiencia computacional razonable
- flexibilidad en la definición de problemas
- verificación y validación
- extensibilidad
Observación. El requerimiento de paralelización está relacionado con el tamaño de los problemas a resolver y no (tanto) con la performance. Está claro que, de tener la posibilidad, resolver ecuaciones en forma paralela es más eficiente en términos del tiempo de pared1 necesario para obtener un resultado. Pero en el SRS, la posibilidad de paralelizar el código se refiere principalmente a la capacidad de poder resolver problemas de tamaño arbitrario que no podrían ser resueltos en serie, principalmente por una limitación de la cantidad de memoria RAM.
Observación. Si bien es cierto que en teoría un algoritmo implementado en cualquier lenguaje Turing-completo podría resolver un sistema de ecuaciones algebraicas de tamaño arbitrario independientemente de la memoria RAM disponible (por ejemplo usando almacenamiento intermedio en dispositivos magnéticos o de estado sólido), no es posible obtener un resultado útil en un tiempo razonable si no se dispone de suficiente memoria RAM para evitar tener que descargar el contenido de esta memoria de alta velocidad de acceso a medios alternativos (out-of-core memory como los mencionados en el paréntesis anterior) cuya velocidad de acceso es varios órdenes de magnitud más lenta.
Observación. Este esquema de definir primero los requerimientos y luego indicar cómo se los satisface evita un sesgo común dentro de las empresas de software que implica hacer algo “fácil para el desarrollador” a costa de que el usuario tenga que hacer algo “más difícil”. Por ejemplo en la mayoría de los programas de elementos finitos para elasticidad lineal es necesario hacer un mapeo entre los grupos de elementos volumétricos y los materiales disponibles, tarea que tiene sentido siempre que haya más de un grupo de elementos volumétricos o más de un material disponible. Pero en los casos donde hay un único grupo de elementos volumétricos (usualmente porque se parte de un CAD con un único volumen) y un único juego de propiedades materiales (digamos un único valor E de módulo de Young y un único \nu para coeficiente de Poisson), el software requiere que el usuario tenga que hacer explícitamente el mapeo aún cuando éste sea único y trivial. Un claro de ejemplo del sesgo “developer-easy/user-hard” que FeenoX no tiene2, ya que el SRS pide que “problemas sencillos tengan inputs sencillos”. En caso de que haya una única manera de asociar volúmenes geométricos a propiedades materiales, FeenoX hace la asociación implícitamente simplificando el archivo de entrada.
Según el pliego, es mandatorio que el software desarrollado sea de código abierto según la definición de la Open Source Initiative. El SDS (apéndice B) comienza indicando que la herramienta FeenoX es
- al software tradicional de ingeniería y
- a las bibliotecas especializadas de elementos finitos
lo que Markdown es
- a Word y
- a LaTeX
respectivamente.
Luego explica que no sólo es de código abierto en el sentido de la OSI sino que también es libre en el sentido de la Free Software Foundation [30], como pide el SRS. La diferencia entre código abierto y software libre es más sutil que práctica, ya que las definiciones técnicas prácticamente coinciden. El punto principal de que el código sea abierto es que permite obtener mejores resultados con mejor performance mientras más personas puedan estudiar el código, escrutarlo y eventualmente mejorarlo [12]. Por otro lado, el software libre persigue un fin ético relacionado con la libertad de poder ejecutar, distribuir, modificar y distribuir las modificaciones del software recibido [17], [28]. En la Sección 4.4.1 discutimos los detalles de estas ideas.
Observación. Ninguno de los dos conceptos, código abierto o software libre, se refiere a la idea de precio. En castellano no debería haber ninguna confusión. Pero en inglés, el sustantivo adjetivado free software se suele tomar como gratis en lugar de libre. Si bien es cierto que la mayoría de las veces la utilización de software libre y abierto no implica el pago de ninguna tarifa directa al autor del programa, el software libre puede tener otros costos indirectos asociados.3 El concepto importante es libertad: la libertad de poder contratar a uno o más programadores que modifiquen el código para que el software se comporte como uno necesita.
Tal como como Unix4 [14] y C5, FeenoX es un “efecto de tercer sistema”6 [13]. De hecho, esta diferencia entre el concepto de código abierto y software libre fue discutida en la referencia [21] durante el desarrollo de la segunda versión del sistema. Una vez más, la Sección 4.4.1 provee una explicación de los conceptos fundamentales y, literalmente, de la filosofía detrás de la idea de software libre.
De las lecciones aprendidas en las dos primeras versiones, la primera un poco naíf pero funcional y la segunda más pretenciosa y compleja (apalancada en la funcionalidad de la primera), hemos convergido al diseño explicado en el SDS del apéndice B donde definimos la filosofía de diseño del software y elegimos una de estas infinitas formas de diseñar una herramienta computacional mencionadas al comienzo de este capítulo. Gran parte de este diseño está basado en la filosofía de programación Unix [13]. En el apéndice B damos ejemplos de cómo son las interfaces para definir un cierto problema y de cómo obtener los resultados. Comparamos alternativas e indicamos por qué hemos decidido diseñar el software de la forma en la que lo hemos hecho y comentamos muy superficialmente las ideas distintivas que tiene FeenoX con respecto a otros programas de elementos finitos desde el punto de vista técnico de programación. Estas características son distintivas del diseño e implementación propuestos y no son comunes. En la jerga de emprendedurismo, serían las unfair advantages del software con respecto a otras herramientas similares.
Observación. El código fuente de FeenoX está en Github en https://github.com/seamplex/feenox/ bajo licencia GPLv3+ (Sección 4.4.1). Consiste en aproximadamente cuarenta y cinco mil líneas de código .·
Observación. El Journal of Open Source Software ha publicado un artículo donde sucintamente se presentan las características distintivas de FeenoX con respecto a otras herramientas libres y abiertas ya existentes [26]. Tanto dicho artículo como esta tesis corresponden a la versión 1.0 del software, que a su vez corresponde al tag v1.0 del repositorio en Github.
4.1 Arquitectura del código
Comencemos preguntándonos qué debemos tener en cuenta para implementar una herramienta computacional que permita resolver ecuaciones en derivadas parciales con aplicación en ingeniería utilizando el método de elementos finitos. Por el momento enfoquémonos en problemas lineales7 como los analizados en los dos capítulos anteriores. Las dos tareas principales son
- construir la matriz global de rigidez \mathsf{K} y el vector \mathbf{b} (o la matriz de masa \mathsf{M}), y
- resolver el sistema de ecuaciones \mathsf{K} \cdot \mathbf{u} = \mathbf{b} (o \mathsf{K} \cdot \mathbf{u} = \lambda \cdot \mathsf{M} \cdot \mathbf{u})
- convertir \mathbf{u} en flujos \psi(\mathbf{x}) y/o \phi(\mathbf{x})
Haciendo énfasis en la filosofía Unix, tenemos que escribir un programa que haga bien una sola cosa8 que nadie más hace y que interactúe con otros que hacen bien otras cosas (regla de composición). En este sentido, nuestra herramienta se tiene que enfocar en los puntos 1 y 3. Pero tenemos que definir quién va a hacer el punto 2 para que sepamos cómo es que tenemos que construir \mathsf{K} y \mathbf{b}.
Las bibliotecas PETSc [3], [4] junto con la extensión SLEPc [7], [15] proveen exactamente lo que necesita una herramienta que satisfaga el SRS siguiendo la filosofía de diseño del SDS. De hecho, en 2010 seleccioné PETSc para la segunda versión del solver neutrónico por la única razón de que era una dependencia necesaria para resolver el problema de criticidad con SLEPc [22], [23]. Con el tiempo, resultó que PETSc proveía el resto de las herramientas necesarias para resolver numéricamente ecuaciones en derivadas parciales en forma portable y extensible.
Otra vez desde el punto de vista de la filosofía de programación Unix, la tarea 1 consiste en un cemento de contacto9 entre la definición del problema a resolver por parte del ingeniero usuario y la biblioteca matemática para resolver problemas ralos10 PETSc [11]. Cabe preguntarnos entonces cuál es el lenguaje de programación adecuado para implementar el diseño del SDS. Aún cuando ya mencionamos que cualquier lenguaje Turing-completo es capaz de resolver un sistema de ecuaciones algebraicas, está claro que no todos son igualmente convenientes. Por ejemplo Assembly o BrainFuck son interesantes en sí mismos (por diferentes razones) pero para nada útiles para la tarea que tenemos que realizar. De la misma manera, en el otro lado de la distancia con respecto al hardware, lenguajes de alto nivel como Python o R también quedan fuera de la discusión por cuestiones de eficiencia computacional. A lo sumo, estos lenguajes interpretados podrían servir para proveer clientes finos11 (ver Sección 4.4.6) a través de APIs12 que puedan llegar a simplificar la definición del (o los) problema(s) que tenga que resolver FeenoX. Para resumir una discusión mucho más compleja, los lenguajes candidatos para implementar la herramienta requerida por el SRS podrían ser
- Fortran
- C
- C++
Según la regla de representación de Unix, la implementación debería poner la complejidad en las estructuras de datos más que en la lógica. Sin embargo, en el área de mecánica computacional, paradigmas de programación demasiado orientados a objetos impactan negativamente en la performance. La tendencia es encontrar un balance, tal como persigue la filosofía desde hace más de dos mil quinientos años a través de la virtud de la prudencia, entre programación orientada a objetos y programación orientada a datos.
Observación. En los últimos años el lenguaje Rust se ha comenzado a posicionar como una alternativa a C para system programming13 debido al requerimiento intrínseco de que todos las referencias deben apuntar a una dirección de memoria virtual válida. A principios de 2023 aparecieron por primera vez líneas de código en Rust en el kernel de Linux. Pero desde el punto de vista de computación de alto rendimiento,14 Rust (o incluso Go) no tienen nada nuevo que aportar con respecto a C.
Tal como explican los autores de PETSc (y coincidentemente Eric Raymond en [13]), C es el lenguaje que mejor se presta a este paradigma:
Why is PETSc written in C, instead of Fortran or C++?
When this decision was made, in the early 1990s, C enabled us to build data structures for storing sparse matrices, solver information, etc. in ways that Fortran simply did not allow. ANSI C was a complete standard that all modern C compilers supported. The language was identical on all machines. C++ was still evolving and compilers on different machines were not identical. Using C function pointers to provide data encapsulation and polymorphism allowed us to get many of the advantages of C++ without using such a large and more complicated language. It would have been natural and reasonable to have coded PETSc in C++; we opted to use C instead.
Fortran fue diseñado en la década de 1950 y en ese momento representó un salto cualitativo con respecto a la forma de programar las incipientes computadoras digitales [9]. Sin embargo, las suposiciones que se han tenido en cuenta con respecto al hardware y a los sistemas operativos sobre los cuales estos programas deberían ejecutarse ya no son válidas. Las revisiones posteriores como Fortran 90 son modificaciones y parches que no resuelven el problema de fondo. En cambio, C fue diseñado a principios de la década 1970 suponiendo arquitecturas de hardware y de sistemas operativos que justamente son las que se emplean hoy en día, tales como
- espacio de direcciones plano15
- procesadores con registros de diferentes tamaños
- llamadas al sistema16
- entrada y salida basada en archivos
- etc.
para correr en entornos Unix, que esencialmente, es el sistema operativo de la vasta mayoría de los servidores de la nube pública, que justa y nuevamente, es lo que perseguimos en esta tesis.
Una vez más, en principio, la misma tarea puede ser implementada en cualquier lenguaje: Fortran podría implementar programación con objetos y C++ podría ser utilizado con un paradigma orientado a datos. Pero lo usual es que código escrito en Fortran sea procedural y basado en estructuras COMMON, resultando difícil de entender y depurar (y mantener y extender). El código escrito en C++ suele ser orientado a objetos y con varias capas de encapsulamiento, polimorfismo, métodos virtuales, re-definición de operadores17 y contenedores enplantillados18 resultando difícil de entender y depurar, tal como indica Linus Torvals en la cita del comienzo del capítulo. De la misma manera que el lenguaje Fortran permite realizar ciertas prácticas que bien utilizadas agregan potencia y eficiencia pero cuyo abuso lleva a código ininteligible (por ejemplo el uso y abuso de bloques COMMON), C++ permite ciertas prácticas que bien utilizadas agregan potencia pero cuyo abuso lleva a código de baja calidad (por ejemplo el uso y abuso de templates, shared_pointers, binds, moves, lambdas, wrappers sobre wrappers, objetos sobre objetos, interfaz sobre interfaz, etc.), a veces en términos de eficiencia, a veces en términos del concepto de Unix compactness [13]:
Compactness is the property that a design can fit inside a human being’s head. A good practical test for compactness is this: Does an experienced user normally need a manual? If not, then the design (or at least the subset of it that covers normal use) is compact.
y usualmente en términos de la regla de simplicidad en la filosofía de Unix:
Add complexity only where you must.
En efecto, Fortran y C++ hacen fácil agregar complejidad innecesaria. En C, no es fácil agregar complejidad innecesaria. Por lo tanto, como bien dice Linus Torvalds una vez más en la cita del comienzo del capítulo, si con esta decisión lo único que pudiésemos hacer es evitar que se pueda agregar gratuitamente complejidad al código, esa ya sería una razón suficiente para tomarla.
4.1.1 Construcción de los objetos globales
Habiendo decidido entonces construir la matriz \mathsf{K} y el vector \mathbf{b} como una “glue layer” implementada en C utilizando una estructura de datos que PETSc pueda entender, preguntémonos ahora qué necesitamos para construir estos objetos. Para simplificar el argumento, supongamos por ahora que queremos resolver la ecuación generalizada de Poisson de la Sección 3.4.1. La matriz global \mathsf{K} proviene de ensamblar las matrices elementales \mathsf{K}_i para todos los elementos volumétricos e_i según la definición 3.23. De la misma manera, el vector global \mathbf{b}_i proviene de ensamblar las contribuciones elementales \mathbf{b}_i tanto de los elementos volumétricos (definición 3.24) como de los elementos de superficie con condiciones de contorno naturales (definición 3.25).
Una posible implementación en pseudo código de alto nivel de esta construcción podría ser la ilustrada en el algoritmo . La aplicación de las condiciones de contorno de Dirichlet según la discusión de la Sección 3.4.1.2 puede ser realizada con el algoritmo o con el algoritmo . En un caso barremos sobre elementos y tenemos que encontrar el índice global asociado a cada nodo local. En otro caso barremos sobre nodos globales pero tenemos que encontrar los elementos asociados al nodo global.
La primera conclusión que podemos extraer es que para problemas escalares, la ecuación a resolver está determinada por la expresión entre llaves de los términos evaluados en cada punto de Gauss para \mathsf{K}_i y para \mathbf{b}_i. Si el problema tuviese más de una incógnita por nodo y reemplazamos las matrices \mathsf{H}_c y \mathsf{B}_i por sus versiones G-aware \mathsf{H}_{Gc} y \mathsf{B}_{Gi}, entonces otra vez la ecuación a resolver está completamente definida por la expresión entre llaves.
Por ejemplo, si quisiéramos resolver difusión de neutrones multigrupo tendríamos que reemplazar el término entre llaves \mathsf{B}_i^T(\mathbf{\xi}_q) \cdot k(\mathbf{x}_q) \cdot \mathsf{B}_i(\mathbf{\xi}_q) en la ecuación 3.49 por \mathsf{L}_i + \mathsf{A}_i - \mathsf{F}_i para obtener la ecuación 3.62
\mathsf{K}_i \leftarrow \mathsf{K}_i + \omega_q \cdot \Big|\det{\left[\mathsf{J}_i\left(\mathbf{\xi}_q\right)\right]}\Big| \cdot \left\{ \mathsf{L}_i(\mathbf{\xi}_q) + \mathsf{A}_i(\mathbf{\xi}_q) - \mathsf{F}_i(\mathbf{\xi}_q)\right\} con las matrices intermedias según la ecuación 3.63
\tag{\ref{eq-LAF}} \begin{aligned} \mathsf{L}_i &= \mathsf{B}_{Gi}^T(\mathbf{\xi}_q) \cdot \mathsf{D}_D(\mathbf{\xi}_q) \cdot \mathsf{B}_{Gi}(\mathbf{\xi}_q) \\ \mathsf{A}_i &= \mathsf{H}_{Gc}^T(\mathbf{\xi}_q) \cdot \mathsf{R}(\mathbf{\xi}_q) \cdot \mathsf{H}_{Gc}(\mathbf{\xi}_q) \\ \mathsf{F}_i &= \mathsf{H}_{Gc}^T(\mathbf{\xi}_q) \cdot \mathsf{X}(\mathbf{\xi}_q) \cdot \mathsf{H}_{Gc}(\mathbf{\xi}_q) \end{aligned} más las contribuciones a la matriz de rigidez para condiciones de Robin. Pero en principio podríamos escribir un algoritmo genérico (¿una cáscara?) que implemente el método de elementos finitos para resolver una cierta ecuación diferencial completamente definida por la expresión dentro de las llaves (¿pasadas como argumentos?).
La segunda conclusión proviene de preguntarnos qué es lo que necesitan los algoritmos , y para construir la matriz de rigidez global \mathsf{K} y el vector \mathbf{b}:
- los conjuntos de cuadraturas de gauss \omega_q, \mathbf{\xi}_q para el elemento e_i
- las matrices canónicas \mathsf{H}_{c}, \mathsf{B}_{c} y \mathsf{H}_{Gc}
- las matrices elementales \mathsf{C}_i, \mathsf{B}_{Gi},
- poder evaluar en \mathbf{x}_q
- las conductividad k(\mathbf{x}) (o las secciones eficaces para construir \mathsf{D}_D(\mathbf{\xi}_q), \mathsf{R}(\mathbf{\xi}_q) y \mathsf{X}(\mathbf{\xi}_q))
- la fuente volumétrica f(\mathbf{x}) (o las fuentes independientes isotrópicas s_{0,g}(\mathbf{\xi}_q))
- las condiciones de contorno p(\mathbf{x}) y g(\mathbf{x}) (o las correspondientes a difusión de neutrones)
Los tres primeros puntos no dependen de la ecuación a resolver. Lo único que se necesita para evaluarlos es tener disponible la topología de la malla no estructurada que discretiza el dominio U \in \mathbb{R}^D a través la posición \mathbf{x}_j \in \mathbb{R}^D de los nodos y la conectividad de cada uno de los elementos e_i.
El cuarto en principio sí depende de la ecuación, pero finalmente se reduce a la capacidad de evaluar
- propiedades de materiales
- condiciones de contorno
en una ubicación espacial arbitraria \mathbf{x}.
Para fijar ideas, supongamos que tenemos un problema de conducción de calor. La conductividad k(\mathbf{x})19 o en general, cualquier propiedad material puede depender de la posición \mathbf{x} porque
- existen materiales con propiedades discontinuas en diferentes ubicaciones \mathbf{x}, y/o
- la propiedad depende continuamente de la posición aún para el mismo material.
De la misma manera, una condición de contorno (sea ésta esencial o natural) puede depender discontinuamente con la superficie donde esté aplicada o continuamente dentro de la misma superficie a través de alguna dependencia con la posición \mathbf{x}.
Entonces, la segunda conclusión es que si nuestra herramienta fuese capaz de proveer un mecanismo para definir propiedades materiales y condiciones de contorno que puedan depender
- discontinuamente según el volumen o superficie al que pertenezca cada elemento (algunos elementos volumétricos pertenecerán al combustible y otros al moderador, algunos elementos superficiales pertenecerán a una condición de simetría y otros a una condición de vacío), y/o
- continuamente en el espacio según variaciones locales (por ejemplo cambios de temperatura y/o densidad, concentración de venenos, etc.)
entonces podríamos resolver ecuaciones diferenciales arbitrarias discretizadas espacialmente con el método de elementos finitos.
4.1.2 Polimorfismo con apuntadores a función
Según la discusión de la sección anterior, podemos diferenciar entre dos partes del código:
Una que tendrá que realizar tareas “comunes”
- en el sentido de que son las mismas para todas las PDEs tal como leer la malla y evaluar funciones en un punto \mathbf{x} arbitrario del espacio
Otra parte que tendrá que realizar tareas particulares para cada ecuación a resolver
- por ejemplo evaluar las expresiones entre llaves en el q-ésimo punto de Gauss del elemento i-ésimo
Definición 4.1 (framework) Llamamos framework a la parte del código que implementa las tareas comunes.
Por decisión de diseño, el problema que FeenoX tiene que resolver tiene que estar completamente definido en el archivo de entrada. Esto es, no se debe necesitar intervención del usuario luego de la ejecución. Entonces, este archivo de entrada debe justamente definir qué clase de ecuación se debe resolver. Como el tipo de ecuación se lee en tiempo de ejecución, el framework debe poder ser capaz de llamar a una u otra (u otra) función que le provea la información particular que necesita: por ejemplo las expresiones entre llaves para la matriz de rigidez y para las condiciones de contorno.
Una posible implementación (ingenua) sería hacer, para cada punto de Gauss de cada uno de los elementos,
De la misma manera, necesitaríamos bloques if (o switch) de este tipo para
- inicializar el problema
- evaluar condiciones de contorno
- calcular resultados derivados (por ejemplo flujos de calor a partir de las temperaturas, tensiones a partir de desplazamientos o corrientes a partir de flujos neutrónicos)
- etc.
Está claro que esto es
- feo,
- ineficiente, y
- difícil de extender
En C++, podríamos diseñar una mejor implementación mediante una jerarquía de clases donde las clases hijas implementarían métodos virtuales que el framework llamaría cada vez que necesite evaluar el término entre llaves. Si bien C no tiene “métodos virtuales”, sí tiene apuntadores a función (que es justamente lo que PETSc usa para implementar polimorfismo ) por lo que podemos usar este mecanismo para lograr una implementación superior, que explicamos a continuación.
Por un lado, sí existe un lugar del código con un bloque if según el tipo de PDE requerida en tiempo de ejecución que consideramos feo, ineficiente y difícil de extender. Pero,
este único bloque de condiciones
ifse ejecutan una sola vez en el momento de analizar gramaticalmente20 el archivo de entrada y lo que hacen es resolver un apuntador a función a la dirección de memoria de una rutina de inicialización particular que el framework debe llamar antes de comenzar a construir \mathsf{K} y \mathbf{b}:if (strcasecmp(token, "laplace") == 0) { feenox.pde.init_parser_particular = feenox_problem_init_parser_laplace; } else if (strcasecmp(token, "mechanical") == 0) { feenox.pde.init_parser_particular = feenox_problem_init_parser_mechanical; } else if (strcasecmp(token, "modal") == 0) { feenox.pde.init_parser_particular = feenox_problem_init_parser_modal; } else if (strcasecmp(token, "neutron_diffusion") == 0) { feenox.pde.init_parser_particular = feenox_problem_init_parser_neutron_diffusion; } else if (strcasecmp(token, "neutron_sn") == 0) { feenox.pde.init_parser_particular = feenox_problem_init_parser_neutron_sn; } else if (strcasecmp(token, "thermal") == 0) { feenox.pde.init_parser_particular = feenox_problem_init_parser_thermal; } else { feenox_push_error_message("unknown problem type '%s'", token); return FEENOX_ERROR; }Estas funciones de inicialización a su vez resuelven los apuntadores a función particulares para evaluar contribuciones elementales volumétricas en puntos de Gauss, condiciones de contorno, post-procesamiento, etc.
El bloque
ifmostrado en el punto anterior es generado programáticamente a partir de un script (regla de Unix de generación, Sección C.14) que analiza (parsea) el árbol del código fuente y, para cada subdirectorio ensrc/pdes, genera un bloqueifautomáticamente. Es fácil ver el patrón que siguen cada una de las líneas del listado en el punto a y escribir un script o macro para generarlo programáticamente. De hecho en la Sección 4.1.4 mostramos una implementación simplificada de dicho script.
Entonces,
Si bien ese bloque sigue siendo feo, es generado y compilado por una máquina que no tiene el mismo sentido estético que nosotros.
Reemplazamos la evaluación de n condiciones
ifpara llamar a una dirección de memoria fija para cada punto de Gauss para cada elemento por una des-referencia de un apuntador a función. En términos de eficiencia, esto es similar (tal vez más eficiente) que un método virtual de C++. Esta des-referencia dinámica no permite que el compilador pueda hacer uninlinede la función llamada, pero el gasto extra21 es muy pequeño. En cualquier caso, el mismo script que “parsea” la estructura ensrc/pdespodría modificarse para generar un binario de FeenoX para cada PDE donde en lugar de llamar a un apuntador a función se llame directamente a las funciones propiamente dichas permitiendo optimización en tiempo de vinculación22 que le permita al compilador hacer elinlinede la función particular (ver Sección 4.4.4).El script que parsea la estructura de
src/pdesen busca de los tipos de PDEs disponibles es parte del pasoautogen.sh(ver la discusión de la Sección 4.1.4) dentro del esquemaconfigure+makede Autotools. Las PDEs soportadas por FeenoX puede ser extendidas agregando un nuevo subdirectorio dentro desrc/pdesdonde ya existentomando uno de estos subdirectorios como plantilla.23 De hecho también es posible eliminar completamente uno de estos directorios en el caso de no querer que FeenoX pueda resolver alguna PDE en particular. De esta forma,
autogen.shpermite extender (o reducir) la funcionalidad del código, que es uno de los puntos solicitados en el SDS. Más aún, sería posible utilizar este mecanismo para cargar funciones particulares desde objetos compartidos24 en tiempo de ejecución (utilizando la funcióndlopenpor ejemplo), incrementando aún más la extensibilidad de la herramienta.
4.1.3 Definiciones e instrucciones
En la Sección 1.2 mencionamos (y en el apéndice B explicamos en detalle) que la herramienta desarrollada es una especie de “función de transferencia” entre uno o más archivos de entrada y cero o más archivos de salida (incluyendo la salida estándar stdout). En la figura 4.1 ilustramos nuevamente esta idea para un cierto problema particular, digamos el Benchmark 3D PWR de IAEA mencionado en el capítulo 1. Este archivo de entrada, que a su vez puede incluir otros archivos de entrada y/o hacer referencia a otros archivos de datos (incluyendo la malla en formato .msh) contiene palabras clave25 en inglés que, por decisión de diseño, deben
- definir completamente el problema de resolver
- ser lo más auto-descriptivas posible
- permitir una expresión algebraica en cualquier lugar donde se necesite un valor numérico
- mantener una correspondencia uno a uno entre la definición “humana” del problema y el archivo de entrada
- hacer que el archivo de entrada de un problema simple sea simple
Estas keywords pueden ser
definiciones26 (sustantivos)
- qué PDE hay que resolver
- propiedades materiales
- condiciones de contorno
- variables, vectores y/o funciones auxiliares
- etc.
instrucciones (verbos)
- leer la malla
- resolver problema
- asignar valores a variables
- calcular integrales o encontrar extremos sobre la malla
- escribir resultados
- etc.
Por un lado, las definiciones se realizan a tiempo de parseo. Por otro lado, Una vez que FeenoX acepta que el archivo de entrada es válido, comienza la ejecución de las instrucciones en el orden indicado en el archivo de entrada. De hecho, FeenoX tiene un apuntador a instrucción27 que recorre una lista a medida que avanza la ejecución de las instrucciones, pero teniendo en cuenta que existe palabras clave (como IF y WHILE) que permiten flujos de ejecución no triviales, especialmente en problemas iterativos, cuasi-estáticos o transitorios:
// sweep the first & last range but minding the conditional blocks
instruction_t *ip = first;
while (ip != last) {
feenox_call(ip->routine(ip->argument));
if (feenox.next_instruction != NULL) {
ip = feenox.next_instruction;
feenox.next_instruction = NULL;
} else {
ip = ip->next;
}
}Por ejemplo, en
f(x) = x^2
PRINT f(1/2) f(1) f(2)la primera línea es una definición (dada por el signo =) y la segunda es una instrucción (verbo PRINT).
En particular, la lectura del archivo de malla es una instrucción y no una definición porque
el nombre del archivo de la malla puede depender de alguna variable cuyo valor deba ser evaluado en tiempo de ejecución con una instrucción previa. Por ejemplo
INPUT_FILE surprise PATH nafems-le1%g.msh round(random(0,1)) READ_MESH surprise PRINT cells$ feenox surprise.fee 18700 $ feenox surprise.fee 18700 $ feenox surprise.fee 32492 $ feenox surprise.fee 32492 $ feenox surprise.fee 18700 $el archivo con la malla en sí puede ser creado internamente por FeenoX con una instrucción previa
WRITE_MESHy/o modificada en tiempo de ejecuciónREAD_MESH square.msh SCALE 1e-3 WRITE_MESH square_tmp.vtk INPUT_FILE tmp PATH square_tmp.vtk READ_MESH tmpen problemas complejos puede ser necesario leer varias mallas antes de resolver la PDE en cuestión, por ejemplo leer una distribución de temperaturas en una malla gruesa de primer orden para utilizarla al evaluar las propiedades de los materiales de la PDE que se quiere resolver. Ver Sección 5.1 y Sección B.3.2.2.
Comencemos con un problema sencillo para luego agregar complejidad en forma incremental. A la luz de la discusión de este capítulo, preguntémonos ahora qué necesitamos para resolver un problema de conducción de calor estacionario sobre un dominio U \in \mathbb{R}^D con un único material:
- definir que la PDE es conducción de calor en D dimensiones
- leer la malla con el dominio U \in \mathbb{R}^D discretizado
- definir la conductividad térmica k(\mathbf{x}) del material
- definir las condiciones de contorno del problema
- construir \mathsf{K} y \mathbf{b}
- resolver \mathsf{K} \cdot \mathbf{u} = \mathbf{b}
- hacer lo que nos haya pedido el usuario en el archivo de entrada con los resultados, por ejemplo
- calcular T_\text{max}
- calcular T_\text{mean}
- calcular el vector flujo de calor q^{\prime \prime}(\mathbf{x}) = -k(\mathbf{x}) \cdot \nabla T
- comparar con soluciones analíticas
- etc.
- escribir los resultados
El problema de conducción de calor más sencillo es un slab unidimensional en el intervalo x \in [0,1] con conductividad uniforme y condiciones de Dirichlet T(0)=0 y T(1)=1 en ambos extremos. Por diseño, el archivo de entrada tiene que ser sencillo (porque dijimos que el problema es sencillo, en el capítulo 5 vamos a ver problemas más complicados con inputs complicados) y tener una correspondencia uno a uno con la definición “humana” del problema:
PROBLEM thermal 1D # 1. definir que la PDE es calor 1D
READ_MESH slab.msh # 2. leer la malla
k = 1 # 3. definir conductividad uniforme igual a uno
BC left T=0 # 4. condiciones de contorno de Dirichlet
BC right T=1 # "left" y "right" son nombres en la malla
SOLVE_PROBLEM # 5. y 6. construir y resolver
PRINT T(0.5) # 7. y 8. escribir en stdout la temperatura en x=0.5En este caso sencillo, la conductividad k fue dada como una variable k con un valor igual a uno. Estrictamente hablando, la asignación fue una instrucción. Pero en el momento de resolver el problema, las funciones particulares de la PDE de conducción de calor (dentro de src/pdes/thermal) buscan una variable llamada k y toman su valor para utilizarlo idénticamente en todos los puntos de Gauss de los elementos volumétricos al calcular el término \mathsf{B}_i^T \cdot k \cdot \mathsf{B}_i.
Si la conductividad no fuese uniforme sino que dependiera del espacio por ejemplo como
k(x) = 1+x entonces el archivo de entrada sería
PROBLEM thermal 1D
READ_MESH slab.msh
k(x) = 1+x # 3. conductividad dada por una función de x
BC left T=0
BC right T=1
SOLVE_PROBLEM
PRINT T(1/2) log(1+1/2)/log(2) # 7. y 8. imprimir el valor numérico y la solución analíticaEn este caso, no hay una variable llamada k sino que hay una función de x (definida con una definición) con la expresión algebraica 1+x. Entonces la rutina particular dentro de src/pde/thermal que evalúa las contribuciones volumétricas elementales de la matriz de rigidez toma dicha función k(x) como la propiedad “conductividad” y la evalúa como \mathsf{B}_i^T(\mathbf{x}_q) \cdot k(\mathbf{x}_q) \cdot \mathsf{B}_i(\mathbf{x}_q). La salida, que por diseño está 100% definida por el archivo de entrada (reglas de Unix de silencio Sección C.11 y de economía Sección C.13) consiste en la temperatura evaluada en x=1/2 junto con la solución analítica \log(1+\frac{1}{2})/\log(2) en dicho punto.
Por completitud, mostramos que también la conductividad podría depender de la temperatura. En este caso particular el problema resulta no lineal. Mencionamos algunas particularidades sin ahondar en detalles. El parser algebraico de FeenoX sabe que k depende de T, por lo que la rutina particular de inicialización de la PDE de conducción de calor marca que el problema debe ser resuelto por PETSc con un objeto SNES en lugar de un KSP como para el caso lineal. FeenoX también calcula el jacobiano necesario para resolver el problema con un método de Newton iterativo, que incluye un término proporcional a \partial k / \partial T:
PROBLEM thermal 1D
READ_MESH slab.msh
k(x) = 1+T(x) # 3. la conductividad ahora depende de T(x)
BC left T=0
BC right T=1
SOLVE_PROBLEM
PRINT T(1/2) sqrt(1+(3*0.5))-1La ejecución de FeenoX sigue también las reglas tradicionales de Unix. Se debe proveer la ruta al archivo de entrada como principal argumento luego del ejecutable. Es un argumento y no como una opción ya que la funcionalidad del programa depende de que se indique un archivo de entrada, por lo que no es “opcional”. Sí se pueden agregar opciones siguiendo las reglas POSIX. Algunas opciones son para FeenoX (por ejemplo --progress o --elements_info y otras son pasadas a PETSc/SLEPc (por ejemplo --ksp_view o --mg_levels_pc_type=sor). Al ejecutar los tres casos anteriores, obtenemos los resultados solicitados con la instrucción PRINT en la salida estándar:
$ feenox thermal-1d-dirichlet-uniform-k.fee
0.5
$ feenox thermal-1d-dirichlet-space-k.fee
0.584945 0.584963
$ feenox thermal-1d-dirichlet-temperature-k.fee
0.581139 0.581139
$ Para el caso de conducción de calor estacionario solamente hay una única propiedad cuyo nombre debe ser k para que las rutinas particulares la detecten como la conductividad k que debe aparecer en la contribución volumétrica. Si el problema tuviese dos materiales diferentes, digamos A y B (es decir, en la malla hubiera algunos elementos asociados a la etiqueta volumétrica A y otros a la etiqueta B) entonces habría dos maneras de definir sus propiedades materiales en FeenoX:
agregando el sufijo
_Ay_Ba la variableko a la funciónk(x), es decirk_A = 1 k_B = 2si k_A = 1 y k_B=2, o
k_A(x) = 1+2*x k_B(x) = 3+4*xsi k_A(x) = 1+2x y k_B(x) = 3+4x.
utilizando una palabra clave
MATERIAL(definición) para ´cada material, del siguiente modoMATERIAL A k=1 MATERIAL B k=2o
MATERIAL A k=1+2*x MATERIAL B k=3+4*x
De esta forma, el framework implementa las dos posibles dependencias de las propiedades de los materiales discutidas:
- continua con el espacio a través de expresiones algebraicas que pueden involucrar funciones definidas por puntos en interpoladas como discutimos en la Sección 4.3, y
- discontinua según el material al que pertenece el elemento.
Con respecto a las condiciones de contorno, la lógica es similar pero ligeramente más complicada. Mientras que a partir del nombre de la propiedad material (incluyendo las fuentes volumétricas) las rutinas particulares pueden evaluar las contribuciones volumétricas, sean a la matriz de rigidez \mathsf{K} a través de la conductividad k o al vector \mathbf{b} a través de la fuente de calor por unidad de volumen q, para las condiciones de contorno se necesita un poco más de información. Supongamos que una superficie tiene una condición de “simetría” y que queremos que la línea del archivo de entrada que la defina sea
BC left symmetrydonde left es el nombre de la entidad superficial definida en la malla y symmetry es una palabra clave que indica qué tipo de condición de contorno tienen los elementos que pertenecen a left. La forma de implementar numéricamente (e incluso físicamente) esta condición de contorno depende de la PDE que estamos resolviendo. No es lo mismo poner una condición de simetría en las ecuaciones de
- poisson generalizada
- elasticidad lineal
- difusión de neutrones
- transporte por S_N
Entonces, si bien las propiedades de materiales pueden ser parseadas por el framework y aplicadas por las rutinas particulares, las condiciones de contorno deben ser parseadas y aplicadas por las rutinas particulares. De todas maneras, la lógica es similar: las rutinas particulares proveen puntos de entrada28 que el framework llama en los momentos pertinentes durante la ejecución de las instrucciones.
Para terminar de ilustrar la idea, consideremos el problema de Reed (discutido en detalle en la Sección 5.2) que propone resolver con S_N un slab uni-dimensional compuesto por varios materiales, algunos con una fuente independiente, otros sin fuente e incluso un material de vacío:
#
# | | | | | |
# m | src= 50 | 0 | 0 | 1 | 0 | v
# i | | | | | | a
# r | tot= 50 | 5 | 0 | 1 | 1 | c
# r | | | | | | u
# o | scat=0 | 0 | 0 | 0.9| 0.9 | u
# r | | | | | | m
# | | | | | |
# | 1 | 2 | 3 | 4 | 5 |
# | | | | | |
# +---------+----+---------+----+---------+-------> x
# x=0 x=2 x=3 x=5 x=6 x=8
PROBLEM neutron_sn DIM 1 GROUPS 1 SN $1
READ_MESH reed.msh
MATERIAL source_abs S1=50 Sigma_t1=50 Sigma_s1.1=0
MATERIAL absorber S1=0 Sigma_t1=5 Sigma_s1.1=0
MATERIAL void S1=0 Sigma_t1=0 Sigma_s1.1=0
MATERIAL source_scat S1=1 Sigma_t1=1 Sigma_s1.1=0.9
MATERIAL reflector S1=0 Sigma_t1=1 Sigma_s1.1=0.9
BC left mirror
BC right vacuum
SOLVE_PROBLEM
FUNCTION ref(x) FILE reed-ref.csv INTERPOLATION steffen
PRINT sqrt(integral((ref(x)-phi1(x))^2,x,0,8))/8La primera línea es una definición (
PROBLEMes un sustantivo) que le indica a FeenoX que debe resolver las ecuaciones S_N en D=1 dimensión con G=1 grupo de energías y utilizando una discretización angular N dada por el primer argumento $1 de la línea de comando luego del nombre del archivo de entrada. De esta manera se pueden probar diferentes discretizaciones con el mismo archivo de entrada, digamosreed.fee$ feenox reed 2 # <- S2 [...] $ feenox reed 4 # <- S4 [...]La segunda línea es una instrucción (el verbo
READ) que indica que FeenoX debe leer la malla donde resolver problema del archivoreed.msh. Si el archivo de entrada se llamarareed.fee, esta línea podría haber sidoREAD_MESH $0.msh. En caso de leer varias mallas, la que define el dominio de la PDE es- la primera de las instrucciones
READ_MESH, o - la definida explícitamente con la palabra clave
MAIN_MESH
- la primera de las instrucciones
El bloque de palabras clave
MATERIALdefinen (con un sustantivo) las secciones eficaces macroscópicas (Sigma) y las fuentes independientes (S). En este caso todas las propiedades son uniformes dentro de cada material.Las siguientes dos líneas definen las condiciones de contorno (
BCes la abreviación boundary condition que es un sustantivo adjetivado): la superficielefttiene una condición de simetría (o espejo) y la superficierighttiene una condición de vacío.La instrucción
SOLVE_PROBLEMle pide a FeenoX que- construya la matriz global \mathsf{K} y el vector \mathbf{b} (pidiéndole a su vez el integrando a las rutinas específicas del subdirectorio
src/pdes/neutron_sn) - que le pida a su vez a PETSc que resuelva el problema \mathsf{K} \cdot \mathbf{u} = \mathbf{b} (como hay fuentes independientes entonces la rutina de inicialización del problema
neutron_snsabe que debe resolver un problema lineal, si no hubiese fuentes y sí secciones eficaces de fisión se resolvería un problema de autovalores con la biblioteca SLEPc) - que extraiga los valores nodales de la solución \mathbf{u} y defina las funciones del espacio \psi_{mg}(x) y \phi_{g}(x). Si
$1fuese2entonces las funciones con la solución seríanpsi1.1(x)psi1.2(x)phi1(x)
$1fuese4entonces seríanpsi1.1(x)psi1.2(x)psi1.3(x)psi1.4(x)phi1(x)
WRITE_MESH, como parte de otras expresiones intermedias, etc. - Si el problema fuese de criticidad, entonces esta instrucción también pondría el valor del factor de multiplicación efectivo k_\text{eff} en una variable llamada
keff.
- construya la matriz global \mathsf{K} y el vector \mathbf{b} (pidiéndole a su vez el integrando a las rutinas específicas del subdirectorio
La siguiente línea define una función auxiliar de la variable espacial x a partir de un archivo de columnas de datos. Este archivo contiene una solución de referencia del problema de Reed. La función
ref(x)puede ser evaluada en cualquier punto x utilizando una interpolación monotónica cúbica de tiposteffen[18].La última línea imprime en la salida estándar una representación ASCII (por defecto utilizando el formato
%gde la instrucciónprintf()de C) del error L_2 cometido por la solución calculada con FeenoX con respecto a la solución de referencia, es decir
\frac{1}{8} \cdot \sqrt{\int_0^8 \left[ \text{ref}(x) - \phi_1(x) \right]^2}
La ejecución de FeenoX con este archivo de entrada para S_2, S_4, S_6 y S_8 da como resultado
$ feenox reed.fee 2
0.0505655
$ feenox reed.fee 4
0.0143718
$ feenox reed.fee 6
0.010242
$ feenox reed.fee 8
0.0102363
$ 4.1.4 Puntos de entrada
La compilación del código fuente usa el procedimiento recomendado por GNU donde el script configure genera los archivos de make29 según
- la arquitectura del hardware (Intel, ARM, etc.)
- el sistema operativo (GNU/Linux, otras variantes, etc.)
- las dependencias disponibles (MPI, PETSc, SLEPc, GSL, etc.)
A su vez, para generar este script configure se suele utilizar el conjunto de herramientas conocidas como Autotools. Estas herramientas generan, a partir de un conjunto de definiciones reducidas dadas en el lenguaje de macros M4, no sólo el script configure sino también otros archivos relacionados al proceso de compilación tales como los templates para los makefiles. Estas definiciones reducidas (que justamente definen las arquitecturas y sistemas operativos soportados, las dependencias, etc.) usualmente se dan en un archivo de texto llamado configure.ac y los templates que indican dónde están los archivos fuente que se deben compilar en archivos llamados Makefile.am ubicados en uno o más subdirectorios. Éstos últimos se referencian desde configure.ac de forma tal que Autoconf y Automake trabajen en conjunto para generar el script configure, que forma parte de la distribución del código fuente de forma tal que un usuario arbitrario pueda ejecutarlo y luego compilar el código con el comando make, que lee el Makefile generado por configure.
Para poder implementar la idea de extensibilidad según la cual FeenoX podría resolver diferentes ecuaciones en derivadas parciales, le damos una vuelta más de tuerca a esta idea de generar archivos a partir de scripts. Para ello empleamos la idea de bootstrapping (figura 4.2), en la cual el archivo configure.ac y/o las plantillas Makefile.am son generadas a partir de un script llamado autogen.sh (algunos autores prefieren llamarlo bootstrap).

bootstrap (también llamado autogen.sh).Este script autogen.sh detecta qué subdirectorios hay dentro del directorio src/pdes y, para cada uno de ellos, agrega unas líneas a un archivo fuente llamado src/pdes/parse.c que hace apuntar un cierto apuntador a función a una de las funciones definidas dentro del subdirectorio. En forma resumida,
for pde in *; do
if [ -d ${pde} ]; then
if [ ${first} -eq 0 ]; then
echo -n " } else " >> parse.c
else
echo -n " " >> parse.c
fi
cat << EOF >> parse.c
if (strcasecmp(token, "${pde}") == 0) {
feenox.pde.parse_problem = feenox_problem_parse_problem_${pde};
EOF
first=0
fi
doneEsto generaría el bloque de ifs feo que ya mencionamos en parse.c:
if (strcasecmp(token, "laplace") == 0) {
feenox.pde.parse_problem = feenox_problem_parse_problem_laplace;
} else if (strcasecmp(token, "mechanical") == 0) {
feenox.pde.parse_problem = feenox_problem_parse_problem_mechanical;
} else if (strcasecmp(token, "modal") == 0) {
feenox.pde.parse_problem = feenox_problem_parse_problem_modal;
} else if (strcasecmp(token, "neutron_diffusion") == 0) {
feenox.pde.parse_problem = feenox_problem_parse_problem_neutron_diffusion;
} else if (strcasecmp(token, "neutron_sn") == 0) {
feenox.pde.parse_problem = feenox_problem_parse_problem_neutron_sn;
} else if (strcasecmp(token, "thermal") == 0) {
feenox.pde.parse_problem = feenox_problem_parse_problem_thermal;
} else {
feenox_push_error_message("unknown problem type '%s'", token);
return FEENOX_ERROR;
}Estas instrucciones son llamadas desde el parser general luego de haber leído la definición PROBLEM. Por ejemplo, si en el archivo de entrada se encuentra esta línea
PROBLEM laplaceentonces el apuntador a función feenox.pde.parse_problem declarado en feenox.h como
int (*parse_problem)(const char *token);apuntaría a la función feenox_problem_parse_problem_laplace() declarada en src/pdes/laplace/methods.h y definida en src/pdes/laplace/parser.c. De hecho, esta función es llamada con el parámetro token conteniendo cada una de las palabras que está a continuación del nombre del problema que el parser general no entienda. En particular, para la línea
PROBLEM neutron_sn DIM 3 GROUPS 2 SN 8lo que sucede en tiempo de parseo es
La palabra clave primaria
PROBLEMes leída (y entendida) por el parser general.El argumento
neutron_snes leído por el bloque generado porautogen.sh. El apuntador a la función globalfeenox.pde.parse_problemse hace apuntar entonces a la función provista ensrc/pdes/neutron_snllamadafeenox_problem_parse_problem_neutron_sn().La palabra clave secundaria
DIMes leída por el parser general. Como es una palabra clave secundaria asociada a la primariaPROBLEMy el parser general la entiende (ya que el framework tiene que saber la dimensión espacial de la ecuación diferencial en derivadas parciales que tiene que resolver, entonces la parsea). Seguidamente, lee el siguiente argumento3(que puede ser una expresión como comentamos más adelante) y sabe que tiene que resolver una ecuación diferencial sobre tres dimensiones espaciales. Esto implica, por ejemplo, definir que las propiedades de los materiales y las soluciones serán funciones de tres argumentos: x, y y z.La palabra clave secundaria
GROUPSes leída por el parser general. Como no es una palabra clave secundaria asociada a la primaraPROBLEM, entonces se llama afeenox.pde.parse_problem(que apunta afeenox_problem_parse_problem_neutron_sn()) con el argumentotokenapuntando aGROUPS.Como el parser particular dentro de
src/pdes/neutron_snsí entiende que la palabra claveGROUPSdefine la cantidad de grupos de energía, lee el siguiente token2(que también puede ser una expresión, ver Sección 4.2), lo entiende como tal y lo almacena en la estructura de datos particular de las rutinas correspondientes aneutron_sn.El control vuelve al parser principal que lee la siguiente palabra clave secundaria
SN. Como tampoco la entiende, vuelve a llamar al parser particular que entiende que debe utilizar las direcciones y pesos de S_8.Una vez más el control vuelve al parser principal, que llega al final de la línea. En este momento, vuelve a llamar al parser específico
feenox_problem_parse_problem_neutron_sn()pero pasandoNULLcomo argumento. En este punto, se considera que el parser específico ya tiene toda la información necesaria para inicializar (al menos una parte) de sus estructuras internas y de las variables o funciones que deben estar disponibles para otras palabras claves genéricas. Por ejemplo, si el problema es neutrónico entonces inmediatamente después de haber parseado completamente la líneaPROBLEMdebe definirse la variablekeffy las funciones con los flujos escalares (y angulares si correspondiere) de forma tal que las siguientes líneas, que serán interpretadas por el parser genérico, entiendan quekeffes una variable y quephi1(x,y,z),psi1.1(x,y,z)ypsi2.8(x,y,z)son expresiones válidas:PRINT "keff = " keff PRINT " rho = " (1-keff)/keff PRINT psi1.1(0,0,0) psi8.2(0,0,0) profile(x) = phi1(x,x,0) PRINT_FUNCTION profile phi1(x,0,0) MIN 0 MAX 20 NSTEPS 100
Dentro de las inicializaciones en tiempo de parseo, cada implementación específica debe resolver el resto de los apuntadores a función que definen los puntos de entrada específicos que el framework principal necesita llamar para
parsear partes específicas del archivo de entrada
- condiciones de contorno
- la palabra clave
WRITE_RESULTSque escribe “automáticamente” los resultados en un archivo de post-procesamiento en formato.msho.vtk. Esto es necesario ya que las rutinas que escriben los resultados son parte del framework general pero dependiendo de la PDE a resolver e incluso de los detalles de la PDE (por ejemplo la cantidad de grupos de energía en un problema neutrónico o la cantidad de modos calculadas en un problema de análisis de modos naturales de oscilación mecánicos).
inicializar estructuras internas
reservar la memoria virtual necesaria con una llamada al sistema operativo30 y construir las matrices y los vectores globales
resolver las ecuaciones discretizadas con PETSc (o SLEPc) según el tipo de problema resultante:
- problema lineal en estado estacionario \mathsf{K} \cdot \mathbf{u} = \mathbf{b} (PETSc KSP)
- problema generalizado de autovalores \mathsf{K} \cdot \mathbf{u} = \lambda \cdot \mathsf{M} \cdot \mathbf{u} (SLEPc EPS)
- problema no lineal en estado estacionario \mathbf{F}(\mathbf{u}) = 0 (PETSc SNES)
- problema transitorio \mathbf{G}(\mathbf{u}, \dot{\mathbf{u}}, t) = 0 (PETSc TS)
calcular campos secundarios a partir de los primarios (ver Sección 4.1.4.5), por ejemplo
- flujos escalares a partir de flujos angulares
- corrientes a partir de flujos neutrónicos
- flujos de calor a partir de temperaturas
- tensiones a partir de deformaciones
- etc.
// parse
int (*parse_problem)(const char *token);
int (*parse_write_results)(mesh_write_t *mesh_write, const char *token);
int (*parse_bc)(bc_data_t *bc_data, const char *lhs, char *rhs);
// init
int (*init_before_run)(void);
int (*setup_pc)(PC pc);
int (*setup_ksp)(KSP ksp);
int (*setup_eps)(EPS eps);
int (*setup_ts)(TS ksp);
// build
int (*element_build_volumetric)(element_t *e);
int (*element_build_volumetric_at_gauss)(element_t *e, unsigned int q);
// solve
int (*solve)(void);
// post
int (*solve_post)(void);
int (*gradient_fill)(void);
int (*gradient_nodal_properties)(element_t *e, mesh_t *mesh);
int (*gradient_alloc_nodal_fluxes)(node_t *node);
int (*gradient_add_elemental_contribution_to_node)(node_t *node, element_t *e, unsigned int j, double rel_weight);
int (*gradient_fill_fluxes)(mesh_t *mesh, size_t j_global);4.1.4.1 Parseo
Cuando se termina la línea de PROBLEM, el parser general llama a parse_problem(NULL) que debe
terminar de rellenar los apuntadores específicos
// virtual methods feenox.pde.parse_bc = feenox_problem_bc_parse_neutron_diffusion; feenox.pde.parse_write_results = feenox_problem_parse_write_post_neutron_diffusion; feenox.pde.init_before_run = feenox_problem_init_runtime_neutron_diffusion; feenox.pde.setup_eps = feenox_problem_setup_eps_neutron_diffusion; feenox.pde.setup_ksp = feenox_problem_setup_ksp_neutron_diffusion; feenox.pde.setup_pc = feenox_problem_setup_pc_neutron_diffusion; feenox.pde.element_build_volumetric = feenox_problem_build_volumetric_neutron_diffusion; feenox.pde.element_build_volumetric_at_gauss = feenox_problem_build_volumetric_gauss_point_neutron_diffusion; feenox.pde.solve_post = feenox_problem_solve_post_neutron_diffusion;inicializar lo que necesita el parser para poder continuar leyendo el problema específico, incluyendo
la definición de variables especiales (por ejemplo los flujos escalares
phi_1,phi_2, etc. y angularespsi_1.1,psi_1.2, ,psi_2.12y las variableskeffysn_alpha) para que estén disponibles para el parser algebraico (ver Sección 4.2)// NOTE: it is more natural to put first the group and then the direction // while in the doc we use $\psi_{mg}$ for (unsigned int g = 0; g < neutron_sn.groups; g++) { for (unsigned int m = 0; m < neutron_sn.directions; m++) { feenox_check_minusone(asprintf(&feenox.pde.unknown_name[sn_dof_index(m,g)], "psi%u.%u", g+1, m+1)); } } // the scalar fluxes phi feenox_check_alloc(neutron_sn.phi = calloc(neutron_sn.groups, sizeof(function_t *))); for (unsigned int g = 0; g < neutron_sn.groups; g++) { char *name = NULL; feenox_check_minusone(asprintf(&name, "phi%u", g+1)); feenox_call(feenox_problem_define_solution_function(name, &neutron_sn.phi[g], FEENOX_SOLUTION_NOT_GRADIENT)); feenox_free(name); } neutron_sn.keff = feenox_define_variable_get_ptr("keff"); neutron_sn.sn_alpha = feenox_define_variable_get_ptr("sn_alpha"); feenox_var_value(neutron_sn.sn_alpha) = 0.5;la colocación de opciones por defecto (¿qué pasa si no hay keywords
GROUPSoSN?)// default is 1 group if (neutron_sn.groups == 0) { neutron_sn.groups = 1; } // default is N=2 if (neutron_sn.N == 0) { neutron_sn.N = 2; } if (neutron_sn.N % 2 != 0) { feenox_push_error_message("number of ordinates N = %d has to be even", neutron_sn.N); return FEENOX_ERROR; } // stammler's eq 6.19 switch(feenox.pde.dim) { case 1: neutron_sn.directions = neutron_sn.N; break; case 2: neutron_sn.directions = 0.5*neutron_sn.N*(neutron_sn.N+2); break; case 3: neutron_sn.directions = neutron_sn.N*(neutron_sn.N+2); break; } // dofs = number of directions * number of groups feenox.pde.dofs = neutron_sn.directions * neutron_sn.groups;la inicialización de direcciones \hat{\mathbf{\Omega}}_m y pesos w_m para S_N
Cuando una línea contiene la palabra clave principal BC tal como
BC left mirror
BC right vacuumentonces el parser principal lee el token siguiente, left y right respectivamente, que intentará vincular con un grupo físico en la malla del problema. Los siguientes tokens, en este caso sólo uno para cada caso, son pasados al parser específico feenox.pde.parse_bc que sabe qué hacer con las palabras mirror y vacuum. Este parser de condiciones de contorno a su vez resuelve uno de los dos apuntadores
int (*set_essential)(bc_data_t *, element_t *, size_t j_global);
int (*set_natural)(bc_data_t *, element_t *, unsigned int q);dentro de la estructura asociada a la condición de contorno según corresponda al tipo de condición.
4.1.4.2 Inicialización
Luego de que el parser lee completamente el archivo de entrada, FeenoX ejecuta las instrucciones en el orden adecuado, opcional y/o posiblemente siguiendo lazos de control y bucles.31 Al llegar a la instrucción SOLVE_PROBLEM, llama al punto de entrada init_before_run() donde
Se leen las expresiones que definen las propiedades de los materiales, que no estaban disponibles en el momento de la primera inicialización después de leer la línea
PROBLEM. Estas propiedades de materiales en general y las secciones eficaces macroscópicas en particular pueden estar dadas por- variables
- funciones del espacio
- la palabra clave
MATERIAL
En este momento de la ejecución todas las secciones eficaces deben estar definidas con nombres especiales. Por ejemplo,
- \Sigma_{tg} =
"Sigma_t%d" - \Sigma_{ag} =
"Sigma_a%d" - \nu\Sigma_{fg} =
"nuSigma_f%d" - \Sigma_{s_0 g \rightarrow g^\prime} =
"Sigma_s%d.%d" - \Sigma_{s_1 g \rightarrow g^\prime} =
"Sigma_s_one%d.%d" - S_g =
"S%d"
Dependiendo de si hay fuentes de fisión y/o fuentes independientes se determina si hay que resolver un problema lineal o un problema de autovalores generalizado. En el primer caso se hace
feenox.pde.math_type = math_type_linear; feenox.pde.solve = feenox_problem_solve_petsc_linear; feenox.pde.has_mass = 0; feenox.pde.has_rhs = 1;y en el segundo
feenox.pde.math_type = math_type_eigen; feenox.pde.solve = feenox_problem_solve_slepc_eigen; feenox.pde.has_mass = 1; feenox.pde.has_rhs = 0;
Luego de esta segunda inicialización, se llama al apuntador feenox.pde.solve que para neutrónica es o bien
feenox_problem_solve_petsc_linear()que construye \mathsf{K} y \mathbf{b} y resuelve \mathsf{K} \cdot \mathbf{u} = \mathbf{b}, ofeenox_problem_solve_slepc_eigen()que construye \mathsf{K} y \mathsf{M} y resuelve \mathsf{K} \cdot \mathbf{u} = \lambda \cdot \mathsf{M} \cdot \mathbf{u}.
Antes de construir y resolver las ecuaciones, se llama a su vez a los apuntadores a función que correspondan
feenox_pde.setup_pc(PC pc)feenox.pde.setup_ksp(KSP kps)feenox.pde.setup_eps(EPS eps)
donde cada problema particular configura el pre-condicionador, el solver lineal y el solver de autovalores en caso de que el usuario no haya elegido algoritmos explícitamente en el archivo de entrada. Si el operador diferencial es elíptico y simétrico (por ejemplo para conducción de calor o elasticidad lineal) tal vez convenga usar por defecto un solver iterativo basado en gradientes conjugados pre-condicionado con multi-grilla geométrica-algebraica32 [2]. En cambio para un operador hiperbólico no simétrico (por ejemplo S_N multigrupo) es necesario un solver más robusto como por ejemplo LU.
4.1.4.3 Construcción
Para construir las matrices globales \mathsf{K} y/o \mathsf{M} y/o el vector global \mathbf{b}, el framework general hace un bucle sobre todos los elementos volumétricos (locales a cada proceso) y, para cada uno de ellos, primero llama al punto de entrada feenox.pde.element_build_volumetric() que toma un apuntador al elemento como único argumento. Cada elemento es una estructura tipo element_t definida en feenox.h como
struct element_t {
size_t index;
size_t tag;
double quality;
double volume;
double area;
double size;
double gradient_weight; // this weight is used to average the contribution of this element to nodal gradients
double *w; // weights of the gauss points time determinant of the jacobian
double **x; // coordinates fo the gauss points
double *normal; // outward normal direction (only for 2d elements)
// matrix with the coordinates (to compute the jacobian)
gsl_matrix *C;
element_type_t *type; // pointer to the element type
physical_group_t *physical_group; // pointer to the physical group this element belongs to
node_t **node; // pointer to the nodes, node[j] points to the j-th local node
cell_t *cell; // pointer to the associated cell (only for FVM)
};Luego el framework general hace un sub-bucle sobre el índice q de los puntos de Gauss y llama a feenox.pde.element_build_volumetric_at_gauss() que toma el apuntador al elemento y el índice q como argumentos:
// if the specific pde wants, it can loop over gauss point in the call
// or it can just do some things that are per-element only and then loop below
if (feenox.pde.element_build_volumetric) {
feenox_call(feenox.pde.element_build_volumetric(this));
}
// or, if there's an entry point for gauss points, then we do the loop here
if (feenox.pde.element_build_volumetric_at_gauss != NULL) {
int Q = this->type->gauss[feenox.pde.mesh->integration].Q;
for (unsigned int q = 0; q < Q; q++) {
feenox_call(feenox.pde.element_build_volumetric_at_gauss(this, q));
}
}Estos dos métodos son responsables de devolver los objetos elementales volumétricos \mathsf{K}_i, \mathsf{M}_i como matrices densas en formato de la GNU Scientific Library gsl_matrix y el vector elemental \mathbf{b}_i como gsl_vector almacenados en los apuntadores globales dentro de la estructura feenox.fem:
// elemental (local) objects
gsl_matrix *Ki; // elementary stiffness matrix
gsl_matrix *Mi; // elementary mass matrix
gsl_matrix *JKi; // elementary jacobian for stiffness matrix
gsl_matrix *Jbi; // elementary jacobian for RHS vector
gsl_vector *bi; // elementary right-hand side vectorObservación. Las matrices jacobianas son necesarias para problemas no lineales resueltos con SNES.
Para el caso de difusión de neutrones, las dos funciones que construyen los objetos elementales son
int feenox_problem_build_volumetric_neutron_diffusion(element_t *e) {
if (neutron_diffusion.space_XS == 0) {
feenox_call(feenox_problem_neutron_diffusion_eval_XS(feenox_fem_get_material(e), NULL));
}
return FEENOX_OK;
}
int feenox_problem_build_volumetric_gauss_point_neutron_diffusion(element_t *e, unsigned int q) {
if (neutron_diffusion.space_XS != 0) {
double *x = feenox_fem_compute_x_at_gauss(e, q, feenox.pde.mesh->integration);
feenox_call(feenox_problem_neutron_diffusion_eval_XS(feenox_fem_get_material(e), x));
}
// elemental stiffness for the diffusion term B'*D*B
double wdet = feenox_fem_compute_w_det_at_gauss(e, q, feenox.pde.mesh->integration);
gsl_matrix *B = feenox_fem_compute_B_G_at_gauss(e, q, feenox.pde.mesh->integration);
feenox_call(feenox_blas_BtCB(B, neutron_diffusion.D_G, neutron_diffusion.DB, wdet, neutron_diffusion.Li));
// elemental scattering H'*A*H
gsl_matrix *H = feenox_fem_compute_H_Gc_at_gauss(e, q, feenox.pde.mesh->integration);
feenox_call(feenox_blas_BtCB(H, neutron_diffusion.R, neutron_diffusion.RH, wdet, neutron_diffusion.Ai));
// elemental fission matrix
if (neutron_diffusion.has_fission) {
feenox_call(feenox_blas_BtCB(H, neutron_diffusion.X, neutron_diffusion.XH, wdet, neutron_diffusion.Fi));
}
if (neutron_diffusion.has_sources) {
feenox_call(feenox_blas_Atb_accum(H, neutron_diffusion.s, wdet, feenox.fem.bi));
}
// for source-driven problems
// Ki = Li + Ai - Xi
// for criticallity problems
// Ki = Li + Ai
// Mi = Xi
feenox_call(gsl_matrix_add(neutron_diffusion.Li, neutron_diffusion.Ai));
if (neutron_diffusion.has_fission) {
if (neutron_diffusion.has_sources) {
feenox_call(gsl_matrix_scale(neutron_diffusion.Fi, -1.0));
feenox_call(gsl_matrix_add(neutron_diffusion.Li, neutron_diffusion.Fi));
} else {
feenox_call(gsl_matrix_add(feenox.fem.Mi, neutron_diffusion.Fi));
}
}
feenox_call(gsl_matrix_add(feenox.fem.Ki, neutron_diffusion.Li));
return FEENOX_OK;
}Luego de hacer el bucle sobre cada punto de Gauss q de cada elemento volumétrico e_i, el framework general se encarga de ensamblar los objetos globales \mathsf{K}, \mathsf{M} y/o \mathbf{b} en formato PETSc a partir de los objetos locales \mathsf{K}_i, \mathsf{M}_i y/o \mathbf{b}_i en formato GSL. En forma análoga, el framework hace otro bucle sobre los elementos superficiales que contienen condiciones de borde naturales y llama al apuntador a función set_natural() que toma como argumentos
un apuntador a una estructura
bc_data_tdefinida comostruct bc_data_t { char *string; enum { bc_type_math_undefined, bc_type_math_dirichlet, bc_type_math_neumann, bc_type_math_robin, bc_type_math_multifreedom } type_math; int type_phys; // problem-based flag that tells which type of BC this is // boolean flags int space_dependent; int nonlinear; int disabled; int fills_matrix; unsigned int dof; // -1 means "all" dofs expr_t expr; expr_t condition; // if it is not null the BC only applies if this evaluates to non-zero int (*set_essential)(bc_data_t *, element_t *, size_t j_global); int (*set_natural)(bc_data_t *, element_t *, unsigned int q); bc_data_t *prev, *next; // doubly-linked list in ech bc_t };que es “rellenada” por el parser específico de condiciones de contorno,
un apuntador al elemento
el índice q del punto de Gauss
Por ejemplo, la condición de contorno natural tipo vacuum de difusión de neutrones es
int feenox_problem_bc_set_neutron_diffusion_vacuum(bc_data_t *this, element_t *e, unsigned int q) {
feenox_fem_compute_x_at_gauss_if_needed_and_update_var(e, q, feenox.pde.mesh->integration, this->space_dependent);
double coeff = (this->expr.items != NULL) ? feenox_expression_eval(&this->expr) : 0.5;
double wdet = feenox_fem_compute_w_det_at_gauss(e, q, feenox.pde.mesh->integration);
gsl_matrix *H = feenox_fem_compute_H_Gc_at_gauss(e, q, feenox.pde.mesh->integration);
feenox_call(feenox_blas_BtB_accum(H, wdet*coeff, feenox.fem.Ki));
return FEENOX_OK;
}Observación. La condición de contorno tipo mirror en difusión, tal como en la ecuación de Laplace o en conducción de calor, consiste en “no hacer nada”.
Las condiciones de contorno esenciales se ponen en el problema luego de haber ensamblado la matriz global \mathsf{A} para transformarla en la matriz de rigidez \mathsf{K} según el procedimiento discutido en la Sección 3.4.1.5. Para ello debemos hacer un bucle sobre los nodos, bien con el algoritmo o con el algoritmo , y poner un uno en la diagonal de la matriz de rigidez y el valor de la condición de contorno en el nodo en el vector del miembro derecho, en la fila correspondiente al grado de libertad global.
Observación. En un problema de autovalores, sólo es posible poner condiciones de contorno homogéneas. En este caso, se puede
- poner un uno en la diagonal de \mathsf{K} y un cero en la diagonal de \mathsf{M}, ó
- poner un uno en la diagonal de \mathsf{M} y un cero en la diagonal de \mathsf{K}
Cuál de las dos opciones es la más conveniente depende del algoritmo seleccionado para la transformación espectral del problema de autovalores a resolver.
La forma de implementar esto en FeenoX para una PDE arbitraria es que para cada nodo que contiene una condición de Dirichlet, el framework llama al apuntador a función set_essential() que toma como argumentos
- un apuntador a la estructura
bc_data_t - un apuntador al elemento (estructura
element_t) - el índice j global del nodo
Para difusión, la condición null se implementa sencillamente como
int feenox_problem_bc_set_neutron_diffusion_null(bc_data_t *this, element_t *e, size_t j_global) {
for (unsigned int g = 0; g < feenox.pde.dofs; g++) {
feenox_call(feenox_problem_dirichlet_add(feenox.pde.mesh->node[j_global].index_dof[g], 0));
}
return FEENOX_OK;
}En S_N, la condición vacuum es ligeramente más compleja ya que debemos verificar que la dirección sea entrante:
int feenox_problem_bc_set_neutron_sn_vacuum(bc_data_t *this, element_t *e, size_t j_global) {
double outward_normal[3];
feenox_call(feenox_mesh_compute_outward_normal(e, outward_normal));
for (unsigned m = 0; m < neutron_sn.directions; m++) {
if (feenox_mesh_dot(neutron_sn.Omega[m], outward_normal) < 0) {
// if the direction is inward set it to zero
for (unsigned int g = 0; g < neutron_sn.groups; g++) {
feenox_call(feenox_problem_dirichlet_add(
feenox.pde.mesh->node[j_global].index_dof[sn_dof_index(m,g)], 0)
);
}
}
}
return FEENOX_OK;
}La condición de contorno mirror es más compleja aún porque implica condiciones multi-libertad33, que deben ser puestas en la matriz de rigidez usando
- Eliminación directa
- Método de penalidad
- Multiplicadores de Lagrange
En su versión actual, FeenoX utiliza el método de penalidad [6]. El framework provee una llamada genérica feenox_problem_multifreedom_add() donde las rutinas particulares deben “registrar” sus condiciones multi-libertad:
int feenox_problem_bc_set_neutron_sn_mirror(bc_data_t *this, element_t *e, size_t j_global) {
double outward_normal[3];
double reflected[3];
double Omega_dot_outward = 0;
double eps = feenox_var_value(feenox.mesh.vars.eps);
feenox_call(feenox_mesh_compute_outward_normal(e, outward_normal));
for (unsigned m = 0; m < neutron_sn.directions; m++) {
if ((Omega_dot_outward = feenox_mesh_dot(neutron_sn.Omega[m], outward_normal)) < 0) {
// if the direction is inward then we have to reflect it
// if Omega is the incident direction with respect to the outward normal then
// reflected = Omega - 2*(Omega dot outward_normal) * outward_normal
for (int d = 0; d < 3; d++) {
reflected[d] = neutron_sn.Omega[m][d] - 2*Omega_dot_outward * outward_normal[d];
}
unsigned int m_prime = 0;
for (m_prime = 0; m_prime < neutron_sn.directions; m_prime++) {
if (fabs(reflected[0] - neutron_sn.Omega[m_prime][0]) < eps &&
fabs(reflected[1] - neutron_sn.Omega[m_prime][1]) < eps &&
fabs(reflected[2] - neutron_sn.Omega[m_prime][2]) < eps) {
break;
}
}
if (m_prime == neutron_sn.directions) {
feenox_push_error_message("cannot find a reflected direction for m=%d (out of %d in S%d) for node %d", m, neutron_sn.directions, neutron_sn.N, feenox.pde.mesh->node[j_global].tag);
return FEENOX_ERROR;
}
double *coefficients = NULL;
feenox_check_alloc(coefficients = calloc(feenox.pde.dofs, sizeof(double)));
for (unsigned int g = 0; g < neutron_sn.groups; g++) {
coefficients[sn_dof_index(m,g)] = -1;
coefficients[sn_dof_index(m_prime,g)] = +1;
}
feenox_call(feenox_problem_multifreedom_add(j_global, coefficients));
feenox_free(coefficients);
}
}
return FEENOX_OK;
}Éstas son luego multiplicadas por un factor de penalidad y sumadas a la matriz de rigidez por el framework general.
4.1.4.4 Solución
Una vez construidos los objetos globales \mathsf{K} y/o \mathsf{M} y/o \mathbf{b}, el framework llama a feenox.pde.solve() que puede apuntar a
feenox_problem_solve_petsc_linear()feenox_problem_solve_petsc_nonlinear()feenox_problem_solve_slepc_eigen()feenox_problem_solve_petsc_transient()
según el inicializador particular de la PDE haya elegido. Por ejemplo, si la variable end_time es diferente de cero, entonces en thermal se llama a trasient(). De otra manera, si la conductividad k depende de la temperatura T, se llama a nonlinear() y si no depende de T, se llama a linear(). En el caso de neutrónica, tanto difusión como S_N, la lógica depende de si existen fuentes independientes o no:
feenox.pde.math_type = neutron_diffusion.has_sources ? math_type_linear : math_type_eigen;
feenox.pde.solve = neutron_diffusion.has_sources ? feenox_problem_solve_petsc_linear : feenox_problem_solve_slepc_eigen;
feenox.pde.has_stiffness = 1;
feenox.pde.has_mass = !neutron_diffusion.has_sources;
feenox.pde.has_rhs = neutron_diffusion.has_sources;4.1.4.5 Post-procesamiento
Luego de resolver el problema discretizado y de encontrar el vector global solución \mathbf{u}, debemos dejar disponibles la solución para que las instrucciones que siguen a SOLVE_PROBLEM, tales como las palabras clave PRINT o WRITE_RESULTS, puedan operar con ellas.
Definición 4.2 (campos principales) Las funciones del espacio que son solución de la ecuación a resolver y cuyos valores nodales provienen de los elementos del vector solución \mathbf{u} se llaman campos principales.
Definición 4.3 (campos secundarios) Las funciones del espacio que dan información sobre la solución del problema cuyos valores nodales provienen de operar algebraica, diferencial o integralmente sobre el vector solución \mathbf{u} se llaman campos secundarios.
| Problema | Campo principal | Campos secundarios |
|---|---|---|
| Conducción de calor | Temperatura | Flujos de calor |
| Elasticidad (formulación u) | Desplazamientos | Tensiones y deformaciones |
| Difusión de neutrones | Flujos escalares | Corrientes |
| Ordenadas discretas | Flujos angulares | Flujos escalares y corrientes |
La tabla 4.1 lista los campos principales y secundarios de algunos tipos de problemas físicos. Los campos principales son “rellenados” por el framework general mientras que los campos secundarios necesitan más puntos de entrada específicos para poder ser definidos.
En efecto, el framework sabe cómo “rellenar” las funciones solución a partir de \mathbf{u} mediante los índices que mapean los grados de libertad de cada nodo espacial con los índices globales. Para ello, como ya vimos, cada inicializador debe “registrar” la cantidad y el nombre de las soluciones según la cantidad de grados de libertad por nodo dado en feenox.pde.dofs.
Por ejemplo, para un problema escalar como thermal, hay un único grado de libertad por nodo por lo que debe haber una única función solución de la ecuación que el inicializador “registró” en el framework como
// thermal is a scalar problem
feenox.pde.dofs = 1;
feenox_check_alloc(feenox.pde.unknown_name = calloc(feenox.pde.dofs, sizeof(char *)));
feenox_check_alloc(feenox.pde.unknown_name[0] = strdup("T"));En difusión de neutrones, la cantidad de grados de libertad por nodo es la cantidad G de grupos de energía, leído por el parser específico en la palabra clave GROUPS. Las funciones solución son phi1, phi2, etc:
// default is 1 group
if (neutron_diffusion.groups == 0) {
neutron_diffusion.groups = 1;
}
// dofs = number of groups
feenox.pde.dofs = neutron_diffusion.groups;
feenox_check_alloc(feenox.pde.unknown_name = calloc(neutron_diffusion.groups, sizeof(char *)));
for (unsigned int g = 0; g < neutron_diffusion.groups; g++) {
feenox_check_minusone(asprintf(&feenox.pde.unknown_name[g], "phi%u", g+1));
}En S_N, la cantidad de grados de libertad por nodo es el producto entre M y G. Las funciones, como mostramos en la Sección 4.1.4.1, son psi1.1, psi2.1, etc. donde el primer índice es g y el segundo es m.
4.2 Expresiones algebraicas
Una característica distintiva de FeenoX es que en cada lugar del archivo de entrada donde se espere un valor numérico, desde la cantidad de grupos de energía después de la palabra clave GROUPS hasta las propiedades de los materiales, es posible escribir una expresión algebraica. Por ejemplo
PROBLEM neutron_diffusion DIMENSIONS 1+2 GROUPS sqrt(4)
MATERIAL fuel nuSigma_f1=1+T(x,y,z) nuSigma_f2=10-1e-2*(T(x,y,z)-T0)^2Esto obedece a una de las primeras decisiones de diseño del código. Parafraseando la idea de Unix “todo es un archivo”, para FeenoX “todo es una expresión”. La explicación se basa en la historia misma de por qué en algún momento de mi vida profesional es que decidí escribir la primera versión de este código, cuya tercera implementación es FeenoX Apéndice D. Luego de la tesis de grado [19] y de la de maestría [20], en el año 2009 busqué en StackOverflow cómo implementar un parser PEMDAS (Parenthesis Exponents Multiplication Division Addition Subtraction) en C. Esa primera implementación solamente soportaba constantes numéricas, por lo que luego agregué la posibilidad de incorporar variables y funciones matemáticas estándar (trigonométricas, exponenciales, etc.) cuyos argumentos son, a su vez, expresiones algebraicas. Finalmente funciones definidas por el usuario (Sección 4.3) e incluso funcionales que devuelven un número real a partir de una expresión (implementadas con la GNU Scientific Library) como por ejemplo
derivación
VAR t' f'(t) = derivative(f(t'),t',t)integración
# this integral is equal to 22/7-pi piapprox = 22/7-integral((x^4*(1-x)^4)/(1+x^2), x, 0, 1)sumatoria
# the abraham sharp sum (twenty-one terms) piapprox = sum(2*(-1)^i * 3^(1/2-i)/(2*i+1), i, 0, 20)búsqueda de extremos en un dimensión
PRINT %.7f func_min(cos(x)+1,x,0,6)búsqueda de raíces en una dimensión
VECTOR kl[5] kl[i] = root(cosh(t)*cos(t)+1, t, 3*i-2,3*i+1)
La forma en la que FeenoX maneja expresiones es la siguiente:
El parser toma una cadena de caracteres y la analiza (parsea, por eso es un parser) para generar un árbol de sintaxis abstracto34 que consiste en una estructura
expr_t// algebraic expression struct expr_t { expr_item_t *items; double value; char *string; // just in case we keep the original string // lists of which variables and functions this expression depends on var_ll_t *variables; function_ll_t *functions; expr_t *next; };que tiene una lista simplemente vinculada35 de estructuras
expr_item_t// individual item (factor) of an algebraic expression struct expr_item_t { size_t n_chars; int type; // defines #EXPR_ because we need to operate with masks size_t level; // hierarchical level size_t tmp_level; // for partial sums size_t oper; // number of the operator if applicable double constant; // value of the numerical constant if applicable double value; // current value // vector with (optional) auxiliary stuff (last value, integral accumulator, rng, etc) double *aux; builtin_function_t *builtin_function; builtin_vectorfunction_t *builtin_vectorfunction; builtin_functional_t *builtin_functional; var_t *variable; vector_t *vector; matrix_t *matrix; function_t *function; vector_t **vector_arg; var_t *functional_var_arg; // algebraic expression of the arguments of the function expr_t *arg; // lists of which variables and functions this item (and its daughters) var_ll_t *variables; function_ll_t *functions; expr_item_t *next; };que pueden ser
- un operador algebraico (
+,-,*,/o^) - una constante numérica (
12.34o1.234e1) - una variable (
tox) - un elemento de un vector (
v[1]op[1+i]) - un elemento de una matriz (
A(1,1)oB(1+i,1+j)) - una función interna como por ejemplo (
sin(w*pi*t)oexp(-x)oatan2(y,x)) - un funcional interno como por ejemplo (
integral(x^2,x,0,1)oroot(cos(x)-x,x,0,1)) - una función definida por el usuario (
f(x,y,z)og(t))
- un operador algebraico (
Cada vez que se necesita el valor numérico de la expresión, se recorre la lista
itemsevaluando cada uno de los factores según su orden de procedencia jerárquica PEMDAS.
Observación. Algunas expresiones como por ejemplo la cantidad de grupos de energía deben poder evaluarse en tiempo de parseo. Si bien FeenoX permite introducir expresiones en el archivo de entrada, éstas no deben depender de variables o de funciones ya que éstas necesitan estar en modo ejecución para tener valores diferentes de cero (tal como las constexpr de C++).
Observación. Los índices de elementos de vectores o matrices y los argumentos de funciones y funcionales son expresiones, que deben ser evaluadas en forma recursiva al recorrer la lista de ítems de una expresión base.
Observación. Los argumentos en la línea de comando $1, $2, etc. se expanden como si fuesen cadenas antes de parsear la expresión.
Esta funcionalidad, entre otras cosas, permite comparar resultados numéricos con resultados analíticos. Como muchas veces estas soluciones analíticas están dadas por series de potencias, el funcional sum() es muy útil para realizar esta comparación. Por ejemplo, en conducción de calor transitoria:
# example of a 1D heat transient problem
# from https://www.math.ubc.ca/~peirce/M257_316_2012_Lecture_20.pdf
# T(0,t) = 0 for t < 1
# A*(t-1) for t > 1
# T(L,t) = 0
# T(x,0) = 0
READ_MESH slab-1d-0.1m.msh DIMENSIONS 1
PROBLEM thermal
end_time = 2
# unitary non-dimensional properties
k = 1
rhocp = 1
alpha = k/rhocp
# initial condition
T_0(x) = 0
# analytical solution
# example 20.2 equation 20.25
A = 1.23456789
L = 0.1
N = 100
T_a(x,t) = A*(t-1)*(1-x/L) + 2*A*L^2/(pi^3*alpha^2) * sum((exp(-alpha^2*(i*pi/L)^2*(t-1))-1)/i^3 * sin(i*pi*x/L), i, 1, N)
# boundary conditions
BC left T=if(t>1,A*(t-1),0)
BC right T=0
SOLVE_PROBLEM
IF t>1 # the analytical solution overflows t<1
PRINT %.7f t T(0.5*L) T_a(0.5*L,t) T(0.5*L)-T_a(0.5*L,t)
ENDIF$ feenox thermal-slab-transient.fee
1.0018730 0.0006274 0.0005100 0.0001174
1.0047112 0.0021005 0.0021442 -0.0000436
1.0072771 0.0036783 0.0037210 -0.0000427
1.0097632 0.0052402 0.0052551 -0.0000150
1.0131721 0.0073607 0.0073593 0.0000014
1.0192879 0.0111393 0.0111345 0.0000048
1.0315195 0.0186881 0.0186849 0.0000032
1.0500875 0.0301491 0.0301466 0.0000025
1.0872233 0.0530725 0.0530700 0.0000025
1.1614950 0.0989193 0.0989167 0.0000026
1.3100385 0.1906127 0.1906102 0.0000026
1.6071253 0.3739997 0.3739971 0.0000026
2.0000000 0.6165149 0.6165123 0.0000026
$4.3 Evaluación de funciones
Tal como las expresiones de la sección anterior, el concepto de funciones es central para FeenoX como oposición y negación definitiva de la idea de “tabla” para dar dependencias no triviales de las secciones eficaces con respecto a
- temperaturas
- quemados
- concentración de venenos
- etc.
según lo discutido en la referencia [21] sobre la segunda versión del código.
Una función está completamente definida por
- un nombre único f,
- la cantidad n de argumentos que toma, y
- por la forma de evaluar el número real f(\mathbf{x}) : \mathbb{R}^n \mapsto \mathbb{R} que corresponde a los argumentos \mathbf{x} \in \mathbb{R}^n.
Las funciones en FeenoX pueden ser
- algebraicas, o
- definidas por puntos
4.3.1 Funciones definidas algebráicamente
En el caso de funciones algebraicas, los argumentos de la definición tienen que ser variables que luego aparecen en la expresión que define la función. El valor de la función proviene de
- asignar a las variables de los argumentos los valores numéricos de la invocación, y luego
- evaluar la expresión algebraica que la define.
Por ejemplo
f(x) = 1/2*x^2
PRINT f(1) f(2)Al evaluar f(1) FeenoX pone el valor de la variable x igual a 1 y luego evalúa la expresión 1/2*x^2 dando como resultado 0.5. En la segunda evaluación, x vale 2 y la función se evalúa como 2.
Si en la expresión aparecen otras variables que no forman parte de los argumentos, la evaluación de la función dependerá del valor que tengan estas variables (que se toman como parámetros) al momento de la invocación. Por ejemplo,
VAR v0
v(x0,t) = x0 + v0*t
PRINT v(0,1)
v0 = 1
PRINT v(0,1)en la primera evaluación obtendremos 0 y en la segunda 1.
Observación. La figura 2.7 que ilustra los primeros armónicos esféricos fue creada por la herramienta de post-procesamiento tridimensional Paraview a partir de un archivo VTK generado por FeenoX con el siguiente archivo de entrada:
READ_MESH sphere.msh
Y00(x,y,z) = sqrt(1/(4*pi))
Y1m1(x,y,z) = sqrt(3/(4*pi)) * y
Y10(x,y,z) = sqrt(3/(4*pi)) * z
Y1p1(x,y,z) = sqrt(3/(4*pi)) * x
Y2m2(x,y,z) = sqrt(15/(4*pi)) * x*y
Y2m1(x,y,z) = sqrt(15/(4*pi)) * y*z
Y20(x,y,z) = sqrt(5/(16*pi)) * (-x^2-y^2+2*z^2)
Y2p1(x,y,z) = sqrt(15/(4*pi)) * z*x
Y2p2(x,y,z) = sqrt(15/(16*pi)) * (x^2-y^2)
WRITE_MESH harmonics.vtk Y00 Y1m1 Y10 Y1p1 Y2m2 Y2m1 Y20 Y2p1 Y2p24.3.2 Funciones definidas por puntos sin topología
Por otro lado, las funciones definidas por puntos pueden ser uni-dimensionales o multi-dimensionales. Las multi-dimensionales pueden tener o no topología. Y todas las funciones definidas por puntos pueden provenir de datos
- dentro del archivo de entrada
- de otro archivo de datos por columnas
- de archivos de mallas (
.msho.vtk) - de vectores de FeenoX (posiblemente modificados en tiempo de ejecución)
De hecho, aunque no provengan estrictamente de vectores (podrían hacerlo con la palabra clave FUNCTION VECTOR), FeenoX provee acceso a los vectores que contienen tanto los valores independientes (puntos de definición) como los valores dependientes (valores que toma la función).
Las funciones definidas por puntos que dependen de un único argumento tienen siempre una topología implícita. Para estos casos, FeenoX utiliza el framework de interpolación unidimensional gsl_interp de la GNU Scientific Library. En principio, en este tipo de funciones el nombre de los argumentos no es importante. Pero el siguiente ejemplo ilustra que no es lo mismo definir f(x) que f(y) ya que de otra manera la instrucción PRINT_FUNCTION daría idénticamente sin(y), con el valor que tuviera la variable y al momento de ejecutar la instrucción PRINT_FUNCTION en lugar del perfil sin(x) que es lo que se busca:
FUNCTION f(x) DATA {
-0.8 sin(-0.8)
0.2 sin(0.2)
1.2 sin(1.2)
2.2 sin(2.2)
3.2 sin(3.2)
}
f_a = vecmin(vec_f_x)
f_b = vecmax(vec_f_x)
PRINT_FUNCTION f f(x)-sin(x) MIN f_a MAX f_b NSTEPS 100Este pequeño archivo de entrada—que además muestra que una función definida por puntos puede usar expresiones algebraicas—fue usado para generar la figura 4.3.
Como mencionamos, las funciones definidas por puntos de varias dimensiones pueden tener o no una topología asociada. Si no la tienen, la forma más simple de interpolar una función de k argumentos f(\mathbf{x}) con \mathbf{x} \in \mathbb{R}^k de estas características es asignar al punto de evaluación \mathbf{x} \in \mathbb{R}^k el valor f_i del punto de definición \mathbf{x}_i más cercano a \mathbf{x}.
Observación. La determinación de cuál es el punto de definición \mathbf{x}_i más cercano a \mathbf{x} se realiza en orden O(\log N) con un árbol k-dimensional36 conteniendo todos los puntos de definición \mathbf{x}_i \in \mathbb{R}^k para i=1,\dots,N. La implementación del k-d tree no es parte de FeenoX sino de una biblioteca externa libre y abierta tipo “header only”.
Observación. La noción de “punto más cercano” involucra una métrica del espacio de definición \mathbb{R}^k. Si las k componentes tienen las mismas unidades, se puede emplear la distancia euclidiana usual. Pero por ejemplo si una componente es una temperatura y otra una presión, la métrica euclidiana depende de las unidades en la que se expresan las componentes por lo que deja de ser apropiada.
Una segunda forma de evaluar la función es con una interpolación tipo Shepard [16], original o modificada. La primera consiste en realizar una suma pesada con alguna potencia p de la distancia del punto de evaluación \mathbf{x} a todos los N puntos de definición de la función
f(\mathbf{x}) = \frac{\sum_{i=1}^N w_i(\mathbf{x}) \cdot f_i}{\sum_{i=1}^N w_i(\mathbf{x})} donde
w_i(\mathbf{x}) = \frac{1}{|\mathbf{x} - \mathbf{x}_i|^p}
La versión modificada consiste en sumar solamente las contribuciones correspondientes a los puntos de definición que se encuentren dentro de una hiper-bola de radio R alrededor del punto de evaluación \mathbf{x} \in \mathbb{R}^k.
Observación. La determinación de qué puntos \mathbf{x}_i están dentro de la hiper-bola de centro \mathbf{x} y de radio R también se realiza con un árbol k-d.
4.3.3 Funciones definidas por puntos con topología implícita
Si los puntos de definición están en una grilla multidimensional estructurada rectangularmente (no necesariamente con incrementos uniformes), entonces FeenoX puede detectar la topología implícita y realizar una interpolación local a partir de los vértices del hiper-cubo que contiene el punto de evaluación \mathbf{x} \in \mathbb{R}^k. Esta interpolación local es similar a la explicada a continuación para el caso de topología explícita mediante una generalización de las funciones de forma para los elementos producto-tensor de primer orden a una dimensión arbitraria k.
Por ejemplo, si tenemos el siguiente archivo con tres columnas
- x_i
- y_i
- f_i = f(x_i,y_i)
-1 -1 -1
-1 0 0
-1 +2 2
0 -1 0
0 0 0
0 +2 0
+3 -1 -3
+3 0 0
+3 +2 +6donde no hay una topología explícita pero sí una rectangular implícita, entonces podemos comparar las tres interpolaciones con el archivo de entrada
FUNCTION f(x,y) FILE hyperbolic-paraboloid.dat INTERPOLATION nearest
FUNCTION g(x,y) FILE hyperbolic-paraboloid.dat INTERPOLATION shepard
FUNCTION h(x,y) FILE hyperbolic-paraboloid.dat INTERPOLATION rectangular
PRINT_FUNCTION f g h MIN -1 -1 MAX 3 2 NSTEPS 40 30para obtener la figura 4.4.
nearest)

nearest)shepard)
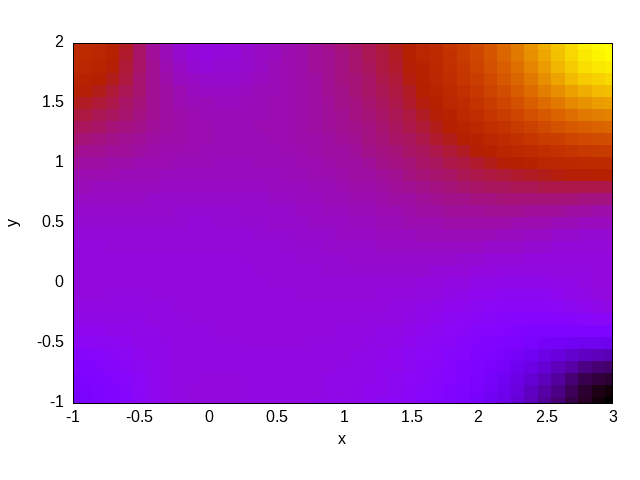
shepard)rectangular)
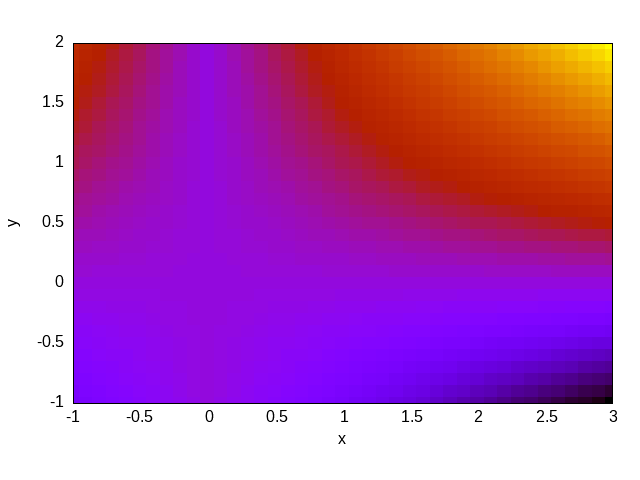
rectangular)4.3.4 Funciones definidas por puntos con topología explícita
Otra forma de definir y evaluar funciones definidas por puntos es cuando existe una topología explícita. Esto es, cuando los puntos de definición forman parte de una malla no estructurada con una conectividad conocida. En este caso, dada una función f(\mathbf{x}), el procedimiento para evaluarla en \mathbf{x} \in \mathbb{R}^2 o \mathbf{x} \in \mathbb{R}^3 es el siguiente:
- Encontrar el elemento e_i que contiene al punto \mathbf{x}
- Encontrar las coordenadas locales \mathbf{\xi} del punto \mathbf{x} en e_i
- Evaluar las J funciones de forma 0 \leq h_j(\mathbf{\xi}) \leq 1 del elemento e_i en el punto \mathbf{\xi}
- Calcular f(\mathbf{x}) a partir de los J valores nodales de definición f_j como
f(\mathbf{x}) = \sum_{j=1}^J h_j(\mathbf{\xi}) \cdot f_j
La forma particular de implementar los puntos 1 y 2 (especialmente el 1) es crucial en términos de performance. FeenoX busca el elemento e_i con una combinación de un k-d tree para encontrar el nodo más cercano al punto \mathbf{x} y una lista de elementos asociados a cada nodo. Una vez encontrado el elemento e_i, resuelve un sistema de ecuaciones de tamaño k (posiblemente no lineal) para encontrar las coordenadas locales \mathbf{\xi} \in \mathbb{R}^k.
De esta manera, si en lugar de tener los puntos de definición completamente estructurado tuviésemos la misma información pero en lugar de incluir el punto de definición f(0,0)=0 tuviésemos f(0.5,0.5)=0.25 pero con la topología asociada (figura 4.5), entonces todavía podemos evaluar f(\mathbf{x}) en cualquier punto arbitrario \mathbf{x} \in [0,1] \times [0,1] para obtener la figura 4.6:
READ_MESH 2d-interpolation-topology.msh DIM 2 READ_FUNCTION f
PRINT_FUNCTION f MIN -1 -1 MAX 3 2 NSTEPS 40 30
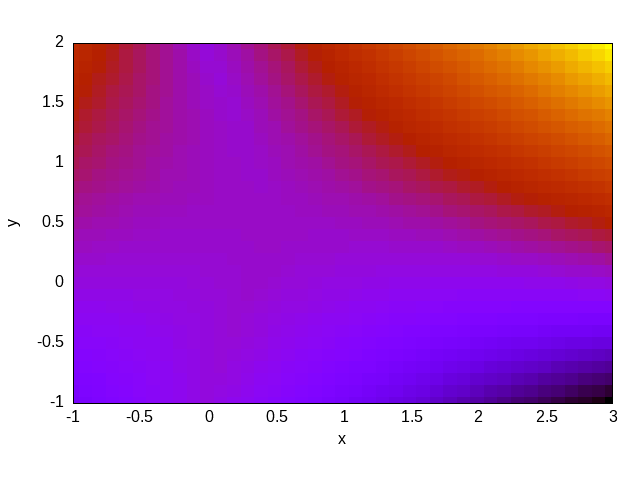
Esta funcionalidad permite realizar lo que se conoce como “mapeo de mallas no conformes” (ver Sección 5.1). Es decir, utilizar una distribución de alguna propiedad espacial (digamos la temperatura) dada por valores nodales en una cierta malla (de un solver térmico) para evaluar propiedades de materiales (digamos la sección eficaz de fisión) en la malla de cálculo. En este caso en particular, los puntos \mathbf{x} donde se requiere evaluar la función definida en la otra malla de definición corresponden a los puntos de Gauss de los elementos de la malla de cálculo. En el caso de estudio de la Sección 5.1 (y en la Sección B.3.2.2 del SDS) profundizamos este concepto.
Observación. Como mencionamos antes, es importante remarcar que para todas las funciones definidas por puntos, FeenoX utiliza un esquema de memoria en la cual los datos numéricos tanto de la ubicación de los puntos de definición \mathbf{x}_j como de los valores f_j de definición están disponibles para lectura y/o escritura como vectores accesibles como expresiones en tiempo de ejecución. Esto quiere decir que esta herramienta puede leer la posición de los nodos de un archivo de malla fijo y los valores de definición de alguna otra fuente que provea un vector del tamaño adecuado, como por ejemplo un recurso de memoria compartida o un socket TCP [24], [25], [29]. Por ejemplo, podemos modificar el valor de definición f(0.5,0.5)=0.25 a f(0.5,0.5)=40 en tiempo de ejecución como
READ_MESH 2d-interpolation-topology.msh DIM 2 READ_FUNCTION f
# modificamos el valor de f(0.5,0.5) de 0.25 a 40
vec_f[5] = 40
PRINT_FUNCTION f MIN -1 -1 MAX 3 2 NSTEPS 40 30para obtener la figura 4.7.
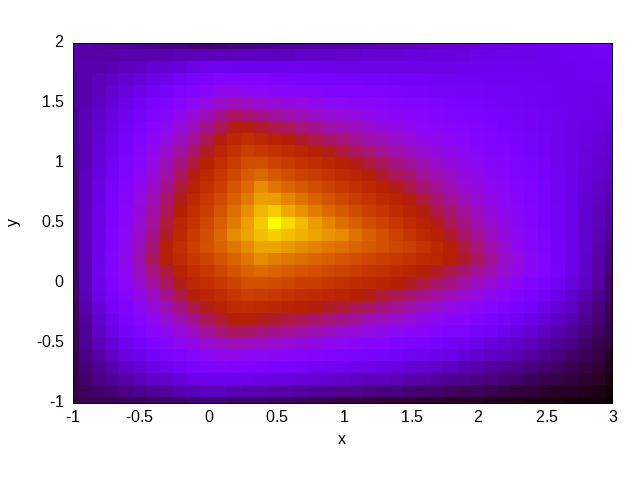
4.4 Otros aspectos
Finalizamos este capítulo pasando revista a algunos aspectos de diversa importancia.
Observación. Hay varios otros aspectos de la implementación que, por cuestiones de límite de espacio y tiempo no explicamos. Por ejemplo, quedan fuera de la discusión que resta
- la forma de calcular campos secundarios con puntos de entrada para diferentes PDEs, incluyendo los algoritmos de extrapolación desde los puntos de Gauss a los nodos y promediado sobre nodos
- detalles de cómo se construyen los objetos algebraicos globales
- la forma de poner las diferentes condiciones de contorno
- la creación de las matrices jacobianas para problemas no lineales
- etc.
4.4.1 Licencia libre y abierta
Quisiera enfatizar en esta sección la importancia del software libre y abierto en general y del relacionado a cálculos de ingeniería en particular. Lo primero que hay que decir es que “software libre” o “código abierto” no implica necesariamente el concepto de gratuidad. Afortunadamente, a diferencia de lo que sucede en inglés, en español los conceptos “libre” y “gratis” se denotan con palabras diferentes. Por lo tanto no debería haber tanta ambigüedad como la hay con el término free software. Sin embargo, más de una docena de años de experiencia me indican que esta diferencia no está suficientemente explicada, especialmente en el ambiente de la ingeniería mecánica donde también se confunden los conceptos de “elementos finitos” con “resolución de las ecuaciones de elasticidad con el método de elementos finitos”.
Si bien estrictamente hablando los conceptos de “software libre” y “código abierto” provienen de etimologías e ideologías diferentes, prácticamente hablando hacen referencia a los mismos conceptos. Y dentro de todos los conceptos asociados, el más importante es el de libertad (freedom en inglés): la licencia de un cierto software es libre y abierta si le otorga al usuario las cuatro libertades fundamentales [28]:37
- The freedom to run the program as you wish, for any purpose (freedom 0).
- The freedom to study how the program works, and change it so it does your computing as you wish (freedom 1). Access to the source code is a precondition for this.
- The freedom to redistribute copies so you can help others (freedom 2).
- The freedom to distribute copies of your modified versions to others (freedom 3). By doing this you can give the whole community a chance to benefit from your changes. Access to the source code is a precondition for this.
Es decir, la importancia del software libre es que los usuarios, que justamente hacen uso del software para que una o más computadoras hagan una cierta tarea—en particular resolver una ecuación diferencial en derivadas parciales—tienen la posibilidad de ver exactamente cómo es que ese software resuelve dichas ecuaciones. E incluso tienen la posibilidad de modificar el código para que las resuelva como ellos quieren. Y acá viene el punto central de la idea. Por más que esos usuarios no tengan los conocimientos necesarios para modificar o incluso para entender el código fuente, tienen la libertad de contratar a alguien para que lo haga por ellos. Es por eso que la idea de libertad es central: en el concepto “free software” la palabra free se debe entender como en “free speech” y no como en “free beer” [30].
Observación. Las libertades dos y tres son esencialmente importantes en el ámbito académico.
Relacionado al movimiento de software libre, que tiene raíces en ideas éticas [17], viene el concepto de código abierto que se basa en consideraciones más bien prácticas: “given enough eyeballs all bugs are shallow” [12]. De hecho esta idea aplica también perfectamente al software de ingeniería: la calidad de un solver open source debería ser, objetivamente hablando, superior a cualquier otra herramienta privativa (en el sentido de que priva a los usuarios de las libertades básicas).
Una vez explicados las bases del software libre y del código abierto, quiero volver a aclarar por qué aquellos que deciden usar este tipo de programas basándose en consideraciones de precios están equivocados. El argumento es que pueden usar solvers “gratuitos” que “hacen lo mismo” que solvers comerciales por los que hay que pagarle una licencia para poder usarlos al desarrollador o, peor aún, a un re-vendedor. Esto hace que este tipo de software, que elimina directamente la libertad básica cero sea clasificado como privativo, como ya explicamos en el párrafo anterior. Pero esto no quiere decir que
- haya que aceptar cualquier tipo de software libre
- el software libre no pueda ser “comercial”
Observación. Como explica técnicamente muy bien pero comunicacionalmente muy mal la Free Software Foundation, el software libre puede tener un modelo de negocios por detrás y ser efectivamente comercial. No hay ningún conflicto ético entre intentar obtener rédito económico escribiendo software y la filosofía de libertad que subyace bajo los ideales del software libre. Luego, es incorrecto usar la palabra “comercial” como antónimo de “software libre”.
Observación. El gerente de ingeniería de una compañía americana que fabrica aleaciones de aluminio especiales con coeficiente de expansión negativo se contactó conmigo porque FeenoX le parecía una herramienta muy interesante para su empresa. Hasta ese momento, FeenoX solamente podía realizar cálculos con un único coeficiente de expansión térmica isotrópico. Pero esta compañía necesitaba realizar cálculos con coeficientes de expansión ortotrópicos. Luego de una propuesta de consultoría, agregué la funcionalidad requerida a cambio de un cierto pago a satisfacción del cliente, con la condición de que el código resultante fuese incorporado a la base de FeenoX con licencia GPLv3+. En forma similar, el autor de la tesis de doctorado [29] me obsequió una botella de cachaça a cambio de haber distribuido el software milonga (la versión anterior de FeenoX) bajo una licencia abierta. Por lo tanto, de primera mano puedo afirmar que el software libre no es incompatible con la idea de software “comercial”.
Observación. Si un programa viene con su código fuente pero el desarrollador original pide que los usuarios firmen un NDA para poder ejecutarlo o impide que personas de cierta nacionalidad puedan usarlo, entonces puede llegar a ser de código abierto pero no es software libre ya que limita la libertad número cero.
Observación. Si un programa de cálculo viene con su código fuente pero éste está escrito en un dialecto de Fortran 77 ininteligible para alguien que haya nacido después de 1980, entonces no es software libre porque limita la libertad número uno.
Para redondear la idea, quisiera citar—una vez más—a Lucio Séneca, que ya nos explicaba la relación entre gratuidad y libertad hace dos mil años durante la Roma Imperial en una carta a su discípulo Lucilio:
“A veces pensamos que sólo se compran las cosas por las que pagamos dinero y llamamos gratuitas a aquellas por las que terminamos sacrificando nuestras personas. Los productos que no estaríamos dispuestos a comprar si a cambio de ellos tuviéramos que entregar nuestra casa o un campo apacible o productivo, estamos muy resueltos a conseguirlos a costa de llenarnos de inquietudes, de peligros, de perder el honor, de perder nuestra libertad y nuestro tiempo; … actuemos, pues, en todos nuestros proyectos y asuntos igual que solemos hacerlo siempre que acudimos a un negocio: consideremos a qué precio se ofrece el objeto que deseamos. Con frecuencia tiene el máximo costo aquel por el que no se paga ningún precio. Podría mostrarte muchos regalos cuya adquisición y aceptación nos ha arrebatado la libertad. Seríamos dueños de nosotros si ellos no fueran nuestros.”
Hay mucho (más de lo que debería) software de cálculo distribuido bajo licencias compatibles con el software libre pero cuya calidad deja mucho que desear y que, sin embargo, es usado por ingenieros con el equivocado concepto de gratuidad. Dejo entonces dos frases populares Argentinas para que cada uno de los amables lectores elija de qué lado se acuesta (con respecto al software libre):
- A caballo regalado no se le miran los dientes.
- Cuando la limosna es grande, hasta el santo desconfía.
Observación. El software FeenoX se distribuye bajo licencia GNU General Public License versión tres o, a elección del usuario, cualquier versión posterior que esté disponible al momento de recibir el software. Esto implica que además de las cuatro libertades, el usuario que recibe una copia del software tiene una restricción: no puede re-distribuir el software si modifica la licencia. Todas las re-distribuciones, tanto con o sin modificaciones, deben ser realizadas bajo la misma licencia con la que fue recibida el software. Este concepto, denominado copyleft (que es otro juego de palabras como lo son Unix, Bash, GNU, less, etc.) hace que el dueño del copyright (en este caso este que escribe) justamente lo use para evitar que alguien que no lo tenga pueda transformar FeenoX en software privativo.
Observación. Siguiendo la recomendación de la organización GNU, al ejecutar feenox con la opción -v (o --version) no solamente se reporta la versión sino también el mensaje de derechos de copia y un resumen de la licencia:
$ feenox -v
FeenoX v1.0.8-g731ca5d
a cloud-first free no-fee no-X uniX-like finite-element(ish) computational engineering tool
Copyright © 2009--2024 Seamplex, https://seamplex.com/feenox
GNU General Public License v3+, https://www.gnu.org/licenses/gpl.html.
FeenoX is free software: you are free to change and redistribute it.
There is NO WARRANTY, to the extent permitted by law.
$ 4.4.2 Filosofía Unix
Por diseño, FeenoX ha sido escrito desde cero teniendo encuentra las ideas de la filosofía de programación Unix resumida en las 17 reglas discutidas el libro “The Art of Unix Programming”38 [13] que explicamos brevemente en el Apéndice C. Los autores originales de Unix explican sus ideas en la referencia [14]. En particular, son de especial aplicación a FeenoX las reglas de
- composición (Sección C.3)
- separación (Sección C.4)
- simplicidad (Sección C.5)
- parsimonia (Sección C.6)
- transparencia (Sección C.7)
- mínima sorpresa (Sección C.10)
- silencio (Sección C.11)
- economía (Sección C.13)
- generación (Sección C.14)
- diversidad (Sección C.16)
En particular, se hace especial énfasis en que el problema a resolver esté completamente definido en un archivo de texto tipo ASCII que pueda ser seguido con un sistema de control de versiones tipo Git. Las mallas, que no son amenas a Git, no son parte del archivo de entrada de FeenoX sino que son referenciadas a través de una ruta a un archivo separado. La idea es que la malla sea generada a partir de otro archivo ameno a Git, como por ejemplo los archivos de entrada de Gmsh o líneas de código en alguno de los lenguajes para los cuales Gmsh provee una API: Python, Julia, C o C++.
Otro ejemplo de ideas de Unix implementadas en FeenoX es la posibilidad de realizar estudios paramétricos leyendo parámetros por la línea de comandos, como explicamos en la Sección 4.4.3 y que utilizamos extensivamente en el capítulo 5. Esto permite que los parámetros a evaluar puedan ser generados por scripts de Bash (que es lo que mayormente usamos en esta tesis) pero también en Python (ver Sección 5.8.3).
La decisión de utilizar bibliotecas numéricas libres, abiertas y bien establecidas también—de alguna manera—responde a una de las ideas de la filosofía Unix: do not repeat yourself! No tiene ningún sentido ponerse a programar los métodos numéricos necesarios para resolver las ecuaciones algebraicas discretizadas desarrolladas en el capítulo 3. No sólo el trabajo ya está hecho y disponible en forma libre y abierta sino que es muy poco probable que el código propio sea más eficiente que el código de PETSc y SLEPc que involucra varios años-hombre de matemáticos y programadores profesionales. Más aún, si algún investigador (que tal vez es uno de estos mismos matemáticos o programadores) descubre algún método o algoritmo más eficiente, una actualización de la biblioteca proveería al solver neutrónico con estos nuevos métodos incrementando su performance casi automáticamente.
Observación. El autor del precondicionador GAMG de PETSc implementó en la versión 3.20 un nuevo esquema de coarsening que, para algunos problemas con ciertas opciones de optimización en el compilador, es más rápido que en la versión 3.19.
Observación. Justamente, las versiones 3.20 y 3.21 de PETSc incluyen contribuciones (corrección de bugs y tests de nuevos features) por parte autor de esta tesis (figura 4.8).
Observación. Al ejecutar feenox sin ninguna opción ni archivo de entrada, éste reportará en la terminal su versión—que incluye el hash del último commit del repositorio Git usado para compilar el ejecutable:
$ feenox
FeenoX v0.3.264-ge4ee9c5
a cloud-first free no-fee no-X uniX-like finite-element(ish) computational engineering tool
usage: feenox [options] inputfile [replacement arguments] [petsc options]
-h, --help display options and detailed explanations of commmand-line usage
-v, --version display brief version information and exit
-V, --versions display detailed version information
--pdes list the types of PROBLEMs that FeenoX can solve, one per line
--elements_info output a document with information about the supported element types
Run with --help for further explanations.
$ Si se incluye la opción -V o --versions entonces se muestra más información sobre el ejecutable propiamente dicho y sus dependencias:
gtheler@chalmers:~$ feenox -V
FeenoX v0.3.267-g07ffa9e
a cloud-first free no-fee no-X uniX-like finite-element(ish) computational engineering tool
Last commit date : Thu Oct 26 12:47:53 2023 -0300
Build date : Mon Oct 30 09:27:21 2023 -0300
Build architecture : linux-gnu x86_64
Compiler version : gcc (Debian 12.2.0-14) 12.2.0
Compiler expansion : gcc -Wl,-z,relro -I/usr/include/x86_64-linux-gnu/mpich -L/usr/lib/x86_64-linux-gnu -lmpich
Compiler flags : -O3 -flto=auto -no-pie
Builder : gtheler@tom
GSL version : 2.7.1
SUNDIALS version : N/A
PETSc version : Petsc Release Version 3.20.0, Sep 28, 2023
PETSc arch : double-int32-release
PETSc options : --download-eigen --download-hdf5 --download-hypre --download-metis --download-mumps --download-parmetis --download-scalapack --download-slepc --with-64-bit-indices=no --with-debugging=no --with-precision=double --with-scalar-type=real COPTFLAGS=-O3 CXXOPTFLAGS=-O3 FOPTFLAGS=-O3
SLEPc version : SLEPc Development GIT revision: v3.19.2-150-g8cd5b338c GIT Date: 2023-09-28 12:25:19 +00004.4.3 Simulación programática
Personalmente no me gusta el término “simulación”,39 pero el concepto de “simulación programática” es lo que se utiliza en la industria para indicar la posibilidad de realizar cálculos de ingeniería sin necesidad de una interfaz gráfica. En el mundo de software de ingeniería, esto involucra que los solvers provean
- una interfaz en lenguaje de alto nivel, o
- una entrada completamente definida en un archivo ASCII
En la mayoría de los programas industriales el camino para proveer “simulación programática” es agregar abstracciones e interfaces a software existente, muchas veces diseñados e implementados hace varias décadas. En FeenoX, esta idea está embebida en el diseño y se provee la “simulación programática” de forma nativa. De hecho en el año 2018 se ha desarrollado un proyecto industrial con la versión 2 del código en el cual un fabricante de implantes de cadera personalizados necesitaba incluir un paso de cálculo mecánico en su workflow automatizado sin intervención manual para definir el problema. La base de diseño del solver fue perfectamente adecuada para poder implementar dicho proyecto con una extrema satisfacción del cliente, acostumbrado a usar programas de cálculo tipo “point and click”.
El hecho de diseñar el software comenzando por la idea de simulación programática en lugar de una interfaz gráfica hace que desarrollar una o más interfaces gráficas sea mucho más sencillo que el camino inverso tomado por las compañías de software de cálculo que se han dado cuenta de las ventajas de la “simulación programática”. Más aún, dado que FeenoX está diseñado para correr en la nube (Sección 4.4.6), es posible entonces desarrollar interfaces web en forma mucho más natural que si no se hubiesen tenido en cuenta todas estas consideraciones. La interfaz, web o desktop, tiene que hacer lo que haría un script programático (tal vez creando la malla y el archivo de entrada .fee) pero en forma interactiva.
Observación. La plataforma CAEplex lanzada en 2017 provee una interfaz web para una versión anterior de FeenoX que permite resolver problemas termo-mecánicos y modales en la nube directamente desde el navegador. Está 100% integrada en la plataforma CAD Onshape, tiene varios miles de usuarios registrados y al momento de la escritura de esta tesis contiene más de diez mil casos resueltos por los usuarios.
Observación. En la lista de trabajos futuros se incluye el desarrollo de interfaces para poder realizar definiciones y ejecutar instrucciones de FeenoX desde lenguajes de scripting, tal como hace Gmsh para Python y Julia.
4.4.4 Performance
Lo primero que hay que decir es que hay mucho “room for improvement” como dicen en inglés, especialmente en temas de performance. En general hay un balance entre requerimientos de CPU y memoria, y cada caso debe ser tratado en forma particular. Por ejemplo, si se almacenan todas las matrices elementales B_{gi} en cada uno de los puntos de Gauss entonces la recuperación de campos secundarios es más rápida a costa de incrementar (tal vez significativamente) la cantidad de memoria RAM necesaria.
Una de las premisas básicas de la optimización de código computacional es medir antes de intentar optimizar. Usando la biblioteca benchmark de Google40 es posible realizar mediciones de secciones del código de FeenoX para comparar diferentes propuestas de optimización como trabajos a futuro:
- efecto de la posibilidad de que el compilar haga inlining de funciones usando link-time optimizations
- eficiencia de acceso a memoria para reducir la cantidad de cache misses
- re-diseñar estructuras de datos siguiendo los paradigmas del diseño orientado a datos (data-oriented design)
- estudiar pros y contras de usar el framework DMPlex [10] de PETSc para manejar la topología de las mallas no estructuradas
Otro de los balances que involucra a la performance de un código es la generalidad vs. la particularidad. Por ejemplo, la posibilidad de seleccionar en tiempo de ejecución cuál de todas las PDEs disponibles se quiere resolver involucra el esquema de apuntadores a función y de puntos de entrada discutidos en la Sección 4.1.4. Esta generalidad hace que no se pueda hacer inlining de estas funciones ya que no se conocen en tiempo de compilación. Es por eso que tal vez se puede mejorar la eficiencia del código si la selección del tipo de PDE se pueda hacer en tiempo de compilación con macros apropiados que puedan optimizar para
- velocidad de ejecución
- memoria
- etc.
por ejemplo generando diferentes ejecutables de FeenoX para particularizaciones de
- el tipo de problema (para evitar apuntadores a función)
- la dimensión del problema (para poder usar arreglos de tamaño fijo en lugar de recurrir a reserva dinámica de memoria)
- mallas con todos los tipos de elementos iguales (para evitar tener que pedir memoria dinámica elemento por elemento)
- tamaño de variables de coma flotante (simple o doble precisión para optimizar memoria)
- etc.
Hay algunos estudios que muestran que para problemas de elasticidad lineal, FeenoX es tan o más rápido que otros programas de código abierto similares, incluso con todo el “room for improvement” de la versión actual.
Es preciso mencionar también que el tema de performance definido como “tiempo de ejecución requerido para resolver un cierto problema” es, por lo menos, ambiguo y difícil de cuantificar. Por ejemplo, consideremos el sistema de templates de C++. Estrictamente hablando, es un lenguaje Turing completo en sí mismo. Por lo tanto, es posible—al menos en teoría—escribir un solver para un problema particular (con la malla y condiciones de contorno embebidos en los templates) implementado 100% como templates de C++. En este caso inverosímil, el tiempo de ejecución sería cero ya que toda la complejidad numérica estaría puesta en la compilación y no en la ejecución.
Si bien este experimento pensado es extremo, hay algunos puntos a tener en cuenta en casos reales. Consideremos el caso de solver algebraicos tipo multi-grid. El tiempo de CPU necesario para resolver un sistema de ecuaciones algebraicas depende fuertemente de la calidad de la malla. Entonces cabe preguntarse: ¿vale la pena “gastar” tiempo de CPU optimizando la calidad de la malla para que el solver converja más rápido? La respuesta va a depender de varias cuestiones, en particular si la misma malla va a ser usada una sola vez o hay varios problemas con diferentes condiciones de contorno que usan la misma malla. Una re-formulación de la conocida conclusión de que no existe el “one size fits all”.
Por sobre este guiso de consideraciones, tenemos la salsa de la regla de economía de Unix. ¿Vale la pena emplear una cantidad x de horas de ingeniería para obtener un beneficio y en términos de recursos computacionales? Pregunta mucho más difícil de responder pero mucho más valiosa y apropiada. En la Sección B.2 ilustramos brevemente esta idea. ¿Cuál es la combinación de herramientas que minimiza el costo total de resolver un laberinto arbitrario (figura B.7) en términos de tiempo de ingeniería más computación?
En relación directa a este concepto de economía de horas de ingeniería por horas de CPU está una de las ideas básicas del diseño de FeenoX. Estrictamente hablando es la regla del silencio de Unix pero fue una de las primeras lecciones aprendidas por este que escribe al trabajar en la industria nuclear con códigos escritos en la década de 1970. Como ya discutimos en el capítulo 1, en esos años cada hora de CPU era mucho más cara que cada hora del ingeniero a cargo de un cálculo. Es por eso que la regla de diseño de esos códigos de cálculo era “escribir en la salida todo lo que se calcula” ya que de necesitar un resultado calculado que no formara parte de la salida obligaría al ingeniero a volver a ejecutar el costoso cálculo. Hoy en día la lógica es completamente opuesta y, en general, es mucho más conveniente volver a realizar un cálculo que tener que buscar agujas en pajares ASCII de varios megabytes de tamaño. Es por eso que en FeenoX la salida está 100% definida en el archivo de entrada. Y de no haber ninguna instrucción tipo PRINT o WRITE_RESULTS, no habrá ninguna salida para el ingeniero.
Observación. Debido a que “todo es una expresión”, FeenoX puede saber luego de parsear el archivo de entrada cuáles de los resultados obtenidos son usados en alguna salida. De esta manera puede tomar decisiones sobre si necesita calcular ciertos parámetros secundarios o no. Por ejemplo, si la función Jx1 no aparece en ninguna expresión (incluyendo instrucciones de salida directa tales como PRINT o WRITE_MESH pero también instrucciones sin salidas directas como INTEGRATE o FIND_EXTREMA) entonces no llamará a las funciones relacionadas al cálculo de corrientes en difusión. Lo mismo sucede para los flujos de calor en el problema térmico y para las tensiones y deformaciones en elasticidad. En este caso la diferencia es aún más importante porque se distinguen los seis componentes del tensor simétrico de Cauchy y las tres tensiones principales \sigma_1, \sigma_2 y \sigma_3 que son los autovalores de dicho tensor. Si el usuario necesita las tensiones principales, sigma1, sigma2 o sigma3 aparecerán en al menos una expresión del archivo de entrada. Si no aparecen (y el parser de FeenoX lo sabe perfectamente) entonces no se desperdician ciclos de CPU calculando resultados que no se utilizan.
De todas maneras, no está de más estudiar detalladamente las formas de reducir el consumo de recursos computacionales para resolver un cierto problema de ingeniería, especialmente si el código va a ser usado masivamente en la nube. A la larga, esto repercutirá en menores costos y en menor consumo energético. Algunos puntos para continuar estudiando:
El algoritmo de construcción de las matrices elementales para S_N es de lo más naïve y replica las ecuaciones algebraicas desarrolladas en el capítulo 3, lo que no suele ser una buena opción desde el punto de vista de análisis de algoritmos [8]. El tamaño de dichas matrices aumenta rápido con N y son, a la vez, esencialmente ralas.
Aún cuando personalmente no comparta la idea de escribir nuevo código de cálculo en Fortran 77, debo reconocer que ésta tiene un punto interesante que debemos considerar. Dado que el modelo de memoria de Fortran 77 es muy limitado, el compilador puede hacer buenas optimizaciones automáticamente porque está seguro de que no habrá apuntadores apuntando a lugares inapropiados o de que no puede haber ciertas condiciones que, aunque poco probables, no permitan emplear algoritmos rápidos o utilizar eficientemente los registros del procesador. Esto en C no sucede automáticamente y es responsabilidad del programador emplear apropiadamente palabras clave reservadas como
constyrestrictpara lograr el mismo nivel de optimización. Se deja también este análisis parte de los trabajos futuros.Para ciertos tipo de problemas matemáticos es conocido que el empleo de GPUs en lugar de CPUs puede reducir costos de ejecución ya que, bien empleadas, las GPUs proveen un factor de reducción de tiempos de cálculo mayor al factor de incremento de costos operacionales. Al utilizar PETSc, FeenoX puede correr los solvers algebraicos en GPU usando opciones en tiempo de ejecución. Si bien este concepto ha sido probado con éxito, se necesita más investigación para poder optimizar la ejecución en GPUs (o incluso en las nuevas APUs de reciente introducción en el mercado).
Las bibliotecas de álgebra de bajo nivel tipo BLAS pueden ganar mucha eficiencia si son capaces de aprovechar las instrucciones tipo SIMD de los procesadores. Para ello es necesario configurar y compilar correctamente PETSc y sus dependencias según la arquitectura sobre la cual se va a ejecutar FeenoX (que no siempre es la arquitectura donde se compila). Hay varias implementaciones de bibliotecas tipo BLAS que PETSc puede usar (por ejemplo OpenBLAS, ATLAS, Netlib, MKL, etc.) cada una con diferentes opciones de compilación y características de optimización.
4.4.5 Escalabilidad
La idea de la escalabilidad de FeenoX viene de la posibilidad de resolver problemas arbitrariamente grandes mediante la paralelización con el estándar MPI [5], [27]. Tal como mostramos y discutimos en el capítulo 5, el hecho de que la ejecución en paralelo haga que el tiempo real (llamado también “tiempo de pared”) necesario para obtener los resultados de resolver una ecuación en derivadas parciales es secundario con respecto al hecho de que la memoria por proceso MPI disminuye a medida que aumenta la cantidad de procesos para un problema de tamaño fijo.
Dicho esto, hay mucho trabajo por hacer en relación a la optimización de las ejecuciones en paralelo y en la interacción con bibliotecas de descomposición de dominios. Pero, como también mostramos en el capítulo 5, la funcionalidad básica de ejecución en paralelo se encuentra disponible en la versión actual de FeenoX.
Observación. Siguiendo las recomendaciones (tanto escritas como orales) de los desarrolladores de PETSc, no se considera en ningún momento la implementación de paralelización basada en OpenMP41. Por un lado no hay evidencia de que este tipo de paralelización basada en threads provea una mejor performance que la paralelización de MPI basada en procesos. Por otro lado, el incremento de la cantidad de threads de OpenMP nunca va a redundar en una disminución de la memoria necesaria para resolver un problema de tamaño fijo ya que los threads son locales y no pueden ser separados en diferentes hosts con diferentes características de memoria RAM.
A modo de ilustración de las características de ejecución con MPI de FeenoX, consideremos el siguiente archivo de entrada (que es parte de los tests de FeenoX):
PRINTF_ALL "Hello MPI World!"La instrucción PRINTF_ALL hace que todos los procesos escriban en la salida estándar los datos formateados con los especificadores de printf las variables indicadas, prefijando cada línea con la identificación del proceso y el nombre del host. Al ejecutar FeenoX con este archivo de entrada con mpiexec en un servidor de AWS apropiadamente configurado para que pueda conectarse a otro y repartir la cantidad de procesos MPI obtendríamos por ejemplo:
ubuntu@ip-172-31-44-208:~/mpi/hello$ mpiexec --verbose --oversubscribe --hostfile hosts -np 4 ./feenox hello_mpi.fee
[0/4 ip-172-31-44-208] Hello MPI World!
[1/4 ip-172-31-44-208] Hello MPI World!
[2/4 ip-172-31-34-195] Hello MPI World!
[3/4 ip-172-31-34-195] Hello MPI World!
ubuntu@ip-172-31-44-208:~/mpi/hello$ Esto es, el host ip-172-31-44-208 crea dos procesos de feenox y a su vez le pide a ip-172-31-34-195 que cree otros dos procesos. Estos podrán entonces resolver un problema en paralelo donde la carga de CPU y la memoria RAM se repartirán entre dos servidores diferentes.
t21 de Gmsh: dos cuadrados mallados con triángulos y descompuestos en 6 particiones.Podemos utilizar el tutorial t21 de Gmsh en el que se ilustra el concepto de DDM (descomposición de dominio o partición de la malla42) para mostrar otro aspecto de cómo funciona la paralelización por MPI en FeenoX. En efecto, consideremos la malla de la figura 4.9 que consiste en dos cuadrados adimensionales de tamaño 1 \times 1 y supongamos que queremos integrar la constante 1 sobre la superficie para obtener como resultado el valor numérico 2:
READ_MESH t21.msh
INTEGRATE 1 RESULT two
PRINTF_ALL "%g" twoEn este caso, la instrucción INTEGRATE se calcula en paralelo donde cada proceso calcula una integral local y antes de pasar a la siguiente instrucción, todos los procesos hacen una operación de reducción mediante la cual se suman todas las contribuciones y todos los procesos obtienen el valor global en la variable two:
$ mpiexec -n 2 feenox t21.fee
[0/2 tom] 2
[1/2 tom] 2
$ mpiexec -n 4 feenox t21.fee
[0/4 tom] 2
[1/4 tom] 2
[2/4 tom] 2
[3/4 tom] 2
$ mpiexec -n 6 feenox t21.fee
[0/6 tom] 2
[1/6 tom] 2
[2/6 tom] 2
[3/6 tom] 2
[4/6 tom] 2
[5/6 tom] 2
$ Para ver lo que efectivamente está pasando, modificamos temporalmente el código fuente de FeenoX para que cada proceso muestre la sumatoria parcial:
$ mpiexec -n 2 feenox t21.fee
[proceso 0] mi integral parcial es 0.996699
[proceso 1] mi integral parcial es 1.0033
[0/2 tom] 2
[1/2 tom] 2
$ mpiexec -n 3 feenox t21.fee
[proceso 0] mi integral parcial es 0.658438
[proceso 1] mi integral parcial es 0.672813
[proceso 2] mi integral parcial es 0.668749
[0/3 tom] 2
[1/3 tom] 2
[2/3 tom] 2
$ mpiexec -n 4 feenox t21.fee
[proceso 0] mi integral parcial es 0.505285
[proceso 1] mi integral parcial es 0.496811
[proceso 2] mi integral parcial es 0.500788
[proceso 3] mi integral parcial es 0.497116
[0/4 tom] 2
[1/4 tom] 2
[2/4 tom] 2
[3/4 tom] 2
$ mpiexec -n 5 feenox t21.fee
[proceso 0] mi integral parcial es 0.403677
[proceso 1] mi integral parcial es 0.401883
[proceso 2] mi integral parcial es 0.399116
[proceso 3] mi integral parcial es 0.400042
[proceso 4] mi integral parcial es 0.395281
[0/5 tom] 2
[1/5 tom] 2
[2/5 tom] 2
[3/5 tom] 2
[4/5 tom] 2
$ mpiexec -n 6 feenox t21.fee
[proceso 0] mi integral parcial es 0.327539
[proceso 1] mi integral parcial es 0.330899
[proceso 2] mi integral parcial es 0.338261
[proceso 3] mi integral parcial es 0.334552
[proceso 4] mi integral parcial es 0.332716
[proceso 5] mi integral parcial es 0.336033
[0/6 tom] 2
[1/6 tom] 2
[2/6 tom] 2
[3/6 tom] 2
[4/6 tom] 2
[5/6 tom] 2
$ Observación. En los casos con M=4 y M=5 procesos, la cantidad de particiones P no es múltiplo de la cantidad de procesos N. De todas maneras, FeenoX es capaz de distribuir la carga entre los N procesos requeridos aunque la eficiencia es menor que en los otros casos.
Al construir los objetos globales \mathsf{K} y \mathsf{M} o \mathbf{b}, FeenoX utiliza un algoritmo similar para seleccionar qué procesos calculan las matrices elementales de cada elemento. Una vez que cada proceso ha terminado de barrer los elementos locales, se le pide a PETSc que ensamble la matriz global enviando información no local a través de mensajes MPI de forma tal de que cada proceso tenga filas contiguas de los objetos globales.
Observación. Cada fila de la matriz global \mathsf{K} corresponde a un grado de libertad asociado a un nodo de la malla.
4.4.6 Ejecución en la nube
Observación. Esta sección podría ser una tesis académica completa (tal vez en el ámbito de tecnologías de informática y comunicaciones) o un informe técnico industrial en sí misma.
FeenoX es una herramienta computacional que ha sido diseñada, haciendo una analogía con el diseño web, como cloud-first (también llamados API-first en la industria del software) y no solamente como cloud-friendly (ver Sección B.1 para una discusión más detallada sobre la diferencia entre este conceptos). Lo segundo quiere decir que la herramienta pueda ser ejecutada en servidores remotos de una forma más o menos sencilla. Pero la primera idea implica conceptos y decisiones de diseño más profundas, que explicamos en esta sección.
Lo primero que hay que decir es que cuando nos referimos a la “nube”, desde un punto de vista de computación de alta performance, estamos haciendo referencia a que en principio disponemos de infinitos recursos computacionales. Haciendo una analogía que termina muy rápido, comparar recursos computacionales on premise con la nube equivale a comparar la generación eléctrica mediante máquinas propias (¿un generador Diesel?) con la posibilidad de tomar energía de la red eléctrica. Esto es, para la mayoría de las aplicaciones, recurrir a recursos computacionales cloud debería ser la primera opción tanto desde el punto de vista técnico como económico.
Para poder usufructuar las ventajas que este tipo de hardware provee, es mandatorio que el software pueda ejecutarse no sólo en forma remota sino que también sea capaz de correr en forma distribuida. Entonces, hay que
- tener todos los hosts en una red particular
- configurar sistemas de nombres de dominios
- diseñar sistemas de archivos de red compartidos
- etc.
En lugar de tener que hacer todo este set-up en forma manual cada vez que se necesite realizar un cálculo de ingeniería, una implementación cloud completa implicaría el desarrollo de una serie de scripts encargados de lanzar y configurar las instancias necesarias para ejecutar dicha simulación. Estos scripts se suelen conocer como “thin clients”, podrían simplemente encargarse de
- lanzar y configurar instancias remotas
- subir archivos de entrada a dichas instancias
- ejecutar las herramientas computacionales (Gmsh, FeenoX, etc.)
- bajar los resultados
Pero también podrían diseñarse clientes (y servidores) más complejos que incluyan llamadas a APIs tipo REST relacionadas a la simulación en sí. Por ejemplo, que manejen temas como
- autenticación
- facturación de horas de CPU
- estimación de los recursos que deben ser lanzados en función del tipo y tamaño del problema a resolver
- estudios paramétricos
- lazos de optimización
- simulaciones condicionalmente encadenadas
- etc.
Si bien esta tesis no abarca a estos clientes (que queda como trabajo a futuro), el diseño de FeenoX es tal que su desarrollo es perfectamente posible y eficiente. De hecho nos referimos a “clientes” en plural porque, tal como pide la regla de Unix de diversidad (Sección C.16), no hay un único tipo de cliente posible sino que hay muchas dependiendo del tipo de problema a resolver. Y como FeenoX justamente es lo suficientemente flexible como para resolver no solamente diferentes PDEs sino también diferentes clases de problema (acoplados, paramétricos, de optimización, etc.) en diferentes entornos (muchos cálculos pequeños, pocos grandes, uno inmenso, etc.) bajo diferentes condiciones (en la industria por una sola persona, en la academia por un equipo, como una plataforma pública as a service, etc.) entonces es de esperar que no haya un cliente que pueda manejar todas las combinaciones en forma óptima. Pero sí lo que se ha tenido en cuenta en el diseño del código computacional de cálculo es que, una vez más siguiendo la filosofía Unix planteada implícitamente durante la década de 1970 [14] pero que sigue siendo extremadamente importante en la década de 2020 a la luz de la arquitectura que “la nube” fue tomando, se debe separar el back end de las capas de abstracción necesarias para llegar a los distintos front ends (figura 4.10) necesarios para su aplicación (regla de separación, Sección C.4) .

Observación. Este párrafo no es trivial. Conozco de primera mano los esfuerzos realizados por una de las empresas de software de cálculo más grandes del mundo (con facturación superior a los 2 mil millones de dólares en 2022 y comprada por 38 mil millones en 2024) que ha intentado agregar esta capa de abstracción a sus solvers existentes con una tasa de suceso tan baja que ha debido comprar una startup que estaba en mejores condiciones de hacerlo por más de cien millones de dólares. En una presentación del gerente encargado de la compra al comité de directores de la empresa (los famosos CxOs), una filmina43 decía literalmente
Desktop solvers design is opposed to API-first solvers.
¿Qué implica todo esto de API-first para un solver neutrónico? Que además de leer uno o más archivos de entrada (o instrucciones en un lenguaje de alto nivel como Python a través de una API) que definan el problema a resolver como suele suceder en la mayoría de los solvers de uso masivo, hay que tener en cuenta que durante la ejecución propiamente dicha se debe poder interactuar con distintas clases de entidades, como por ejemplo
- una interfaz de usuario web
- un sistema de logueo distribuido y compartido
- un reportero de estado bajo demanda por email, sms, whatsapp, telegram, etc.
Luego el back-end debe ser lo suficientemente flexible como para poder reportar su estado y sus eventos con un horizonte de observabilidad mucho mayor que el que se necesitaba en 1970 cuando se diseñaron muchas de las herramientas de uso nuclear (y no nuclear) industrial.
Especialmente importante es el manejo y reporte de errores. Mi experiencia profesional dice que los usuarios hacen gala de su denominación y usan el software de formas que no pueden ser tenidas en cuenta ni por un único desarrollador ni por un equipo de programadores profesionales. Algunas de estas formas tienen sentido y deben ser manejadas por el software. Pero la gran mayoría simplemente son entradas que no tienen sentido (y que justamente por eso no han sido tenidas en cuenta por los desarrolladores). Por lo tanto constantemente aparecen nuevos errores que deben ser reportados en forma humanamente entendible. Entonces tanto el back-end como la capa de abstracción deben ser, una vez más, lo suficientemente flexibles para manejar casos inesperados.
Para terminar, resaltamos que una de las varias maneras de hacer el deployment involucra utilizar la tecnología de contenedores. FeenoX es completamente Docker-friendly en el sentido de que el código puede ser
- obtenido desde el repositorio
- compilado (con las opciones particulares de optimización apropiadas para el hardware donde se va a terminar ejecutando el binario) y
- ejecutado
con líneas de comando estándar de Unix como mostramos en la Sección 4.4.8.
4.4.7 Extensibilidad
Uno de los requerimientos del Sofware Design Requirements del apéndice B es que la herramienta computacional desarrollada pueda ser extensible. El esquema por el cual es posible agregar nuevas ecuaciones diferenciales en derivadas parciales a resolver con el método de elementos finitos con apuntadores a función ya ha sido explicado durante este capítulo. Esta es una característica distintiva que no es común en el mundo del software de elementos finitos, excepto en aquellas herramientas avanzadas como FEniCSx que permiten dar la forma débil de la ecuación a resolver en el archivo de entrada [1].
De todas maneras, si bien FeenoX tiene funcionalidades que no han sido discutidas en detalle en esta tesis (por ejemplo el hecho de poder resolver sistemas de ecuaciones algebraicas-diferenciales que mostramos brevemente en la Sección 5.11), hay muchas otras características que serían deseables en una herramienta de este tipo que no están implementadas. Pero, en principio, la arquitectura del código permite que el desarrollo de temas como
- solución de PDEs discretizadas espacialmente con volúmenes finitos en lugar de elementos finitos
- esquemas espaciales de alto orden
- manejo de elementos estructurales (beam, truss, shell, plate) para resolver problemas de elasticidad
- análisis modales con amortiguación que pueden dar lugar a soluciones complejas
- neutrónica cinético-espacial
Observación. El Ing. Nuclear Ramiro Vignolo ha desarrollado
- una prueba de concepto para resolver neutrónica a nivel de celda con el método de probabilidad de colisiones y
- un solver de redes termohidráulicas 1D en estado estacionario
en la segunda versión del código, mostrando que ya era posible la extensibilidad en la arquitectura anterior aún cuando todavía no era éste uno de los puntos de la base de diseño.
En las conclusiones del capítulo 6 hacemos un listado extensivo de posibles características que podrían ser implementadas sin necesidad de realizar grandes refactorizaciones al código base.
Observación. Como ya hemos explicado en la Sección 4.4.1, FeenoX se distribuye bajo licencia GPLv3 o posterior. Técnicamente hablando (en el sentido leguleyo), el “o posterior” es por extensibilidad (Sección C.17).
4.4.8 Integración continua
Una de las tantas prácticas que se han puesto de moda en la última década en la industria del software que realmente agrega calidad al código resultante (al contrario que las otras modas como el sustantivo scrum y el adjetivo agile) es la llamada integración continua. Esta práctica involucra primero generar y luego automatizar muchos pasos de prueba del código antes de liberar públicamente las versiones.

Como ya mencionamos, el desarrollo de FeenoX se realiza en un repositorio Git alojado en Github (figura 4.11), pero que puede ser clonado y replicado libremente (siguiendo la licencia GPLv3+). Cada commit al repositorio tiene un hash asociado que, como también ya hemos mencionado, es reportado por el binario feenox tanto si se ejecuta sin argumentos como si se ejecuta con la opción -v (o --version). Más aún, la opción -V (o --versions) da no sólo el hash sino también la fecha y hora del último commit del repositorio utilizado para compilar el binario. De esta forma es posible vincular un ejecutable cualquiera encontrado “en la naturaleza”44 con el estado instantáneo del código fuente a través del hash (ayudándose de la fecha reportada por -V).
Observación. A lo largo de la historia del desarrollo de las tres versiones del código hemos utilizado los siguientes sistemas de control de versiones
- Subversion
svn - Bazaar
bzr - Mercurial
hg
Al comienzo del desarrollo (2009) estuvimos a punto de emplear CVS, pero nos decidimos por svn por considerar que cvs era muy anticuado.45
Además del target all en el Makefile que compila el ejecutable, existe un target check que ejecuta una serie de scripts que corresponden al paso de testeo siguiendo el esquema de Autotools. Éste consiste en un conjunto de casos de prueba. Cada uno de ellos ejecuta feenox con diferentes archivos de entrada y compara la salida con resultados pre-definidos. Si la comparación no es exitosa (o si hay algún problema en tiempo de ejecución como por ejemplo una falta de segmentación) entonces el test se marca como fallado. Muchos de estos casos de prueba resuelven problemas cuyo resultado es conocido, sea porque tiene solución analítica o porque su solución numérica está bien establecida. Pero otros casos son arbitrarios y el resultado “de referencia” se utiliza para saber si alguna modificación posterior a la introducción de dicho test hace que el código arroje un resultado diferente. En el caso de que uno de estos casos—conocidos como “tests de regresión”46—falle, se debe
- identificar el commit que hace que el test falle (el procedimiento usual es usar la facilidad de “bisección” de Git)
- analizar si la falla del test es debido a un error en el commit o debido a que el resultado de referencia era incorrecto
- modificar el código o el resultado de referencia
- volver a ejecutar el target
check
Empleando la característica “Actions” de Github, cuando cada uno de las ramas secundarias se une (¿mergea?) a la rama principal (main branch) se crea un servidor virtual básico con Ubuntu (porque no hay imágenes de Debian disponibles) y luego, en forma automática,
se clona el repositorio
git clone https://github.com/seamplex/feenoxse instalan las dependencias necesarias desde Apt
sudo apt-get install -y libgsl-dev libsundials-dev petsc-dev slepc-dev gmshse hace el bootstrapping (figura 4.2), configuración y compilación del código
./autogen.sh && ./configure && makese ejecuta el conjunto de tests y, en caso de al menos uno falle, se reporta el archivo de log
make check || (cat ./test-suite.log && exit 1)
De esta manera, cualquier persona del mundo puede ver a través de la interfaz de Github los commits en los cuales al menos unos de los tests ha fallado (figura 4.12). Pero además, en caso de que algún commit en el branch main no pase los tests, la plataforma le envía un correo electrónico a los administradores del proyecto avisándole de esta situación para que se puedan tomar las decisiones apropiadas.
Si bien el comando make check ejecuta más de 350 casos, el código aún no está instrumentado para medir cuántas líneas son efectivamente “cubiertas” por los tests. Este trabajo de implementar lo que se conoce como medir el “code coverage” en la jerga de integración continua queda como trabajo a futuro (capítulo 6). De la misma manera, también queda como trabajo a futuro diseñar un conjunto de tests que corran bajo la herramienta de desarrollo valgrind para detectar sistemáticamente potenciales problemas con el manejo de memoria, incluyendo
- escrituras en direcciones de memoria no reservadas,
- des-referenciación de punteros inválidos, y/o
- pérdidas de memoria.47
4.4.9 Documentación
El 100% de la documentación, incluyendo
- el sitio web seamplex.com/feenox
- el README del repositorio Git
- el manual descriptivo (en formato Texinfo)
- la referencia completa (en formato HTML y PDF)
- la página de manual de Unix (figura 4.13)
- el Sofware Requirements Specification
- el Sofware Design Specification
- los ejemplos
- esta misma tesis
provienen de texto escrito en Markdown. Luego mediante scripts específicamente diseñados, se crean los distintos documentos en los formatos apropiados con la herramienta Pandoc.
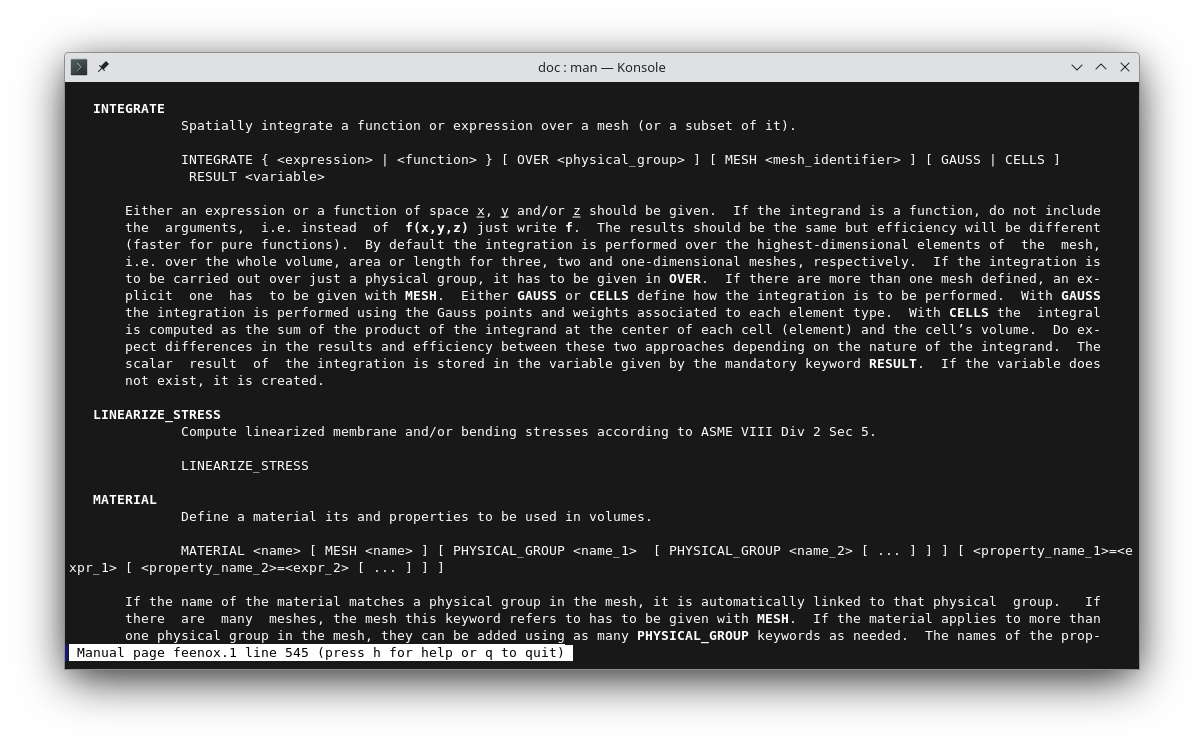
man feenoxToda la documentación en Markdown (aún el fuente del sitio web, incluyendo ejemplos, tutoriales, etc.) forma parte del repositorio de FeenoX. El script que genera los archivos finales en HTML y en PDF inserta en el pie de cada página el hash y la fecha del último commit. De esta manera, si aparece un PDF en Scribd, uno puede saber cabalmente a qué versión de FeenoX se refiere.
El manual de referencia que indica los argumentos que toman las palabras clave, las variables especiales de cada PDE, las funciones internas, etc. provienen de comentarios especiales en el código fuente que comienzan con tres barras hacia adelante (en lugar de los comentarios regulares que usan dos barras). Estos comentarios incluyen meta-datos en un cierto formato que luego un script parsea y genera automáticamente texto en Markdown que luego es compilado al formato final. Por ejemplo,

INTEGRATE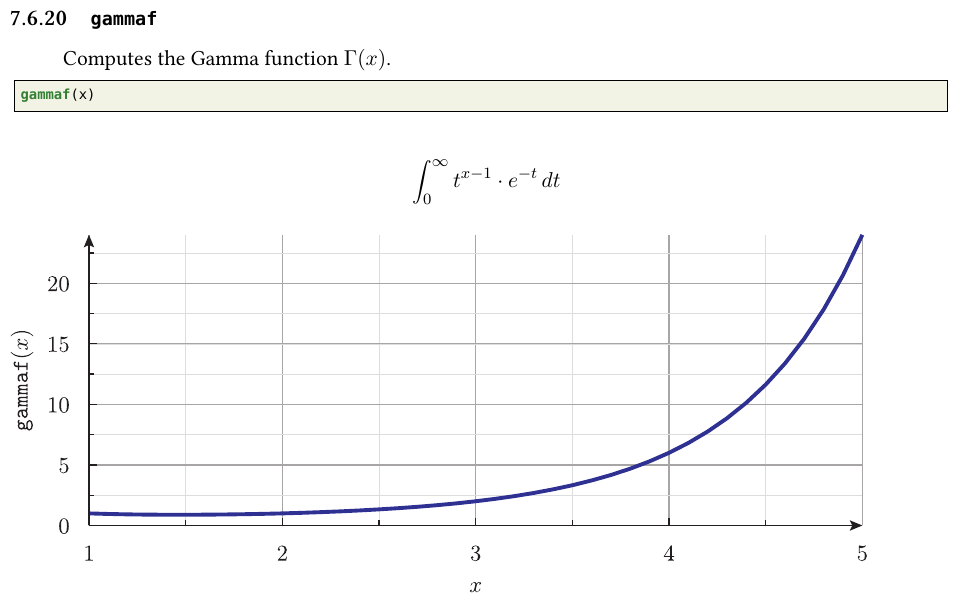
gammaf
derivative
keff y sn_alphapalabras clave
///kw_pde+INTEGRATE+usage { <expression> | <function> } ///kw_pde+INTEGRATE+detail Either an expression or a function of space $x$, $y$ and/or $z$ should be given. ///kw_pde+INTEGRATE+detail If the integrand is a function, do not include the arguments, i.e. instead of `f(x,y,z)` just write `f`. ///kw_pde+INTEGRATE+detail The results should be the same but efficiency will be different (faster for pure functions). char *token = feenox_get_next_token(NULL); if ((mesh_integrate->function = feenox_get_function_ptr(token)) == NULL) { feenox_call(feenox_expression_parse(&mesh_integrate->expr, token)); }funciones internas
///fn+gammaf+desc Computes the Gamma function $\Gamma(x)$. ///fn+gammaf+usage gammaf(x) ///fn+gammaf+math \int_0^\infty t^{x-1} \cdot e^{-t} \, dt ///fn+gammaf+plotx 1 5 1e-1 1 5 1 0 25 5 0.5 2.5 double feenox_builtin_gammaf(expr_item_t *f) { double x = feenox_expression_eval(&f->arg[0]); return (x <= 0) ? 1 : gsl_sf_gamma(x); }funcionales
///fu+derivative+usage derivative(f(x), x, a, [h], [p]) ///fu+derivative+desc Computes the derivative of the expression $f(x)$ ///fu+derivative+desc given in the first argument with respect to the variable $x$ ///fu+derivative+desc given in the second argument at the point $x=a$ given in ///fu+derivative+desc the third argument using an adaptive scheme. ///fu+derivative+desc The fourth optional argument $h$ is the initial width ///fu+derivative+desc of the range the adaptive derivation method starts with. ///fu+derivative+desc The fifth optional argument $p$ is a flag that indicates ///fu+derivative+desc whether a backward ($p < 0$), centered ($p = 0$) or forward ($p > 0$) ///fu+derivative+desc stencil is to be used. ///fu+derivative+desc This functional calls the GSL functions ///fu+derivative+desc `gsl_deriv_backward`, `gsl_deriv_central` or `gsl_deriv_forward` ///fu+derivative+desc according to the indicated flag $p$. ///fu+derivative+desc Defaults are $h = (1/2)^{-10} \approx 9.8 \times 10^{-4}$ and $p = 0$. ///fu+derivative+math \left. \frac{d}{dx} \Big[ f(x) \Big] \right|_{x = a} double feenox_builtin_derivative(expr_item_t *a, var_t *var_x) {variables especiales de S_N
///va_neutron_sn+keff+desc The effective multiplication factor\ $k_\text{eff}$. neutron_sn.keff = feenox_define_variable_get_ptr("keff"); ///va_neutron_sn+sn_alpha+desc The stabilization parameter\ $\alpha$ for $S_N$. neutron_sn.sn_alpha = feenox_define_variable_get_ptr("sn_alpha"); feenox_var_value(neutron_sn.sn_alpha) = 0.5;
dan lugar a la documentación final en PDF ilustrada en la figura 4.14.
Como algunos párrafos de documentación aparecen en más de un único lugar en la documentación entonces hay un esquema de inclusión de archivos de Markdown manejado por un filtros escritos en Lua. Un pequeño ejemplo puede aparecer
- en el README
- en la descripción en Texinfo
- en el SDS
- en el manual de referencia
- etc.
Por ejemplo, las instrucciones para clonar el repositorio y hacer el bootstrapping, la configuración y la compilación están en
- el README principal (que a su vez es el index de la página web),
- en las instrucciones de compilación detalladas, y
- en la sección de “downloads” de la página web.
Observación. La documentación de FeenoX se distribuye bajo los términos de la GNU Free Documentation License v1.3, o cualquier versión posterior.
Del inglés wall time.↩︎
Sabiendo que esta afirmación tiene los sesgos de confirmación, disponibilidad y supervivencia del autor.↩︎
El gerente de sistemas de una empresa de ingeniería y construcción me dijo que por un tema de costos ellos preferían usar un servidor SQL privativo antes que uno libre: “es más caro pagarle al que sabe dónde poner el punto y coma en el archivo de configuración que pagar la licencia y configurarlo con el mouse”.↩︎
A principios de 1960, los Bell Labs en EEUU llegaron a desarrollar un sistema operativo que funcionaba bien, así que decidieron encarar MULTICS (MULTiplexed Information and Computing Service). Como terminó siendo una monstruosidad, empezaron UNIX (UNiplexed Information and Computing System) que es lo que quedó bien.↩︎
A fines de 1960, también en los Bell Labs, llegaron a desarrollar un un lenguaje de programación A que funcionaba bien, así que decidieron encarar B. Como terminó siendo una monstruosidad, empezaron C que es lo que quedó bien.↩︎
Del inglés third-system effect.↩︎
Si el problema fuese no lineal o incluso transitorio, la discusión de esta sección seguiría siendo válida para la construcción de la matriz jacobiana global necesaria para aplicar cada iteración del algoritmo de Newton-Raphson (o similar).↩︎
Do only one thing but do it well.↩︎
En el sentido del inglés glue layer.↩︎
Del inglés sparse.↩︎
Del inglés thin clients.↩︎
Del inglés Application Programming Interface.↩︎
No hay traducción de este término. En el año 2008, se propuso una materia en el IB con este nombre en inglés. El consejo académico decidió traducirla y nombrarla como “programación de sistemas”. Ni el nombre elegido ni el ligeramente más correcto “programación del sistema” tienen la misma denotación que el concepto original system programming↩︎
Del inglés high-performance computing (HPC).↩︎
Del inglés flat address space.↩︎
Del inglés system calls.↩︎
Del inglés operator overloading.↩︎
Del inglés templated containers.↩︎
Si la conductividad dependiera de la temperatura T el problema sería no lineal. Pero en el paso k e la iteración de Newton tendríamos k(\mathbf{T}_k(\mathbf{x})=k_k(\mathbf{x}) por lo que la discusión sigue siendo válida.↩︎
Del inglés parse.↩︎
Del inglés overhead.↩︎
Del inglés link-time optimization.↩︎
Del inglés template↩︎
Del inglés shared objects↩︎
Del inglés keywords.↩︎
La etimología de la palabra “definición” proviene de “dar fin”, es decir, “dar límite” o delimitar qué es lo que queda dentro de la definición y qué no.↩︎
Del inglés instruction pointer.↩︎
Del inglés entry points.↩︎
Del inglés make files.↩︎
Del inglés allocate with a system call.↩︎
Del inglés loop↩︎
Del inglés geometric algebraic multi-grid.↩︎
Del inglés multi-freedom.↩︎
Del inglés abstract syntax tree.↩︎
Del inglés single-linked list.↩︎
Del inglés k-dimensional tree.↩︎
Cita textual de “What is Free Software?” de la Free Software Foundation que nos hace acordar a la explicación de la ley cero de la termodinámica: The reason they are numbered 0, 1, 2 and 3 is historical. Around 1990 there were three freedoms, numbered 1, 2 and 3. Then we realized that the freedom to run the program needed to be mentioned explicitly. It was clearly more basic than the other three, so it properly should precede them. Rather than renumber the others, we made it freedom 0.↩︎
Este título es un juego de palabras donde Eric Raymond le responde a la obra clásica (e inconclusa al momento de la escritura de esta tesis) de Donald Knuth “The Art of Computer Programming” [8].↩︎
Buscar online el blog post “Say modeling not simulation” de 2017 para una explicación.↩︎
Ver repositorio https://github.com/seamplex/feenox-benchmark.↩︎
No confundir con OpenMPI que es una de las varias implementaciones del estándar MPI y que sí es soportada por FeenoX.↩︎
Del inglés mesh partitioning.↩︎
Por supuesto que “filmina” es un anacronismo deliberado. Fue una presentación hecha en un software privativo que no quisiera nombrar para no alentar a nadie a que lo use. Pero justamente, mi opinión personal es que el hecho de que la política de la compañía era usar este software privativo para hacer presentaciones es el que la ha impedido lograr desarrollar la capa de abstracción por la que han debido comprar una startup que hacía sus presentaciones con los macros Beamer de LaTeX.↩︎
Del inglés in the wild.↩︎
El autor de esta tesis llegó a usar CVS en el siglo pasado.↩︎
Del inglés regression tests.↩︎
Del inglés memory leaks↩︎