5 Resultados

FeenoX has releases with a proper tarball! It has INSTALL, ./configure and just compiles. Wow. Yeah, these are free software basics, but majority of the sim software (some discrete circuit simulators included!) I’ve tried fail on most of these points. So thanks for making quality software!

Tibor ‘Igor2’ Palinkas, maintainer of the open source PCB editor pcb-rnd

Es el “tocate una que sepamos todos” de S_N.

Dr. Ignacio Márquez Damián, sobre el problema de Reed (2023)

En este capítulo mostramos diez problemas resueltos con la herramienta computacional FeenoX descripta en el capítulo 4 que ilustran algunas de sus características particulares. Cada uno de estos diez problemas no puede ser resuelto con un solver neutrónico a nivel núcleo que no soporte alguno de los cuatro puntos distintivos de FeenoX:

Filosofía Unix, integración en scripts y simulación programática
Mallas no estructuradas
Ordenadas discretas (además de difusión)
Paralelización en varios nodos de cálculo con MPI

Problema	a	b	c	d
Mapeo en mallas no conformes (5.1)	●	●		◓
El problema de Reed (5.2)	○	◓	●
Benchmark PWR IAEA (5.3)	◓	●		◓
El problema de Azmy (5.4)	●	●	●	○
Benchmarks de Los Alamos (5.5)	●	◓	●
Slab a dos zonas (5.6)	●	●
Reactor cubo-esfera (5.7)	●	●
El problema de los pescaditos (5.8)	●	●	○
MMS con el Stanford bunny (5.9)	●	●	○	○
PHWR vertical con barras inclinadas (5.10)	●	●	●	●

●

requerido

◓

recomendado

○

opcional

Observación. Excepto el primer problema de la Sección 5.1, este capítulo se centra en resolver neutrónica a nivel de núcleo tanto con difusión como con ordenadas discretas. En el documento Software Design Specification del apéndice B se pueden encontrar otro tipo de problemas que ilustran cómo FeenoX resuelve los requerimientos del apéndice A. En la página web de FeenoX, en particular en el apartado de ejemplos, se pueden encontrar más problemas resueltos divididos por tipo de ecuación en derivadas parciales (conducción de calor, elasticidad lineal, análisis modal, neutrónica por difusión, neutrónica por ordenadas discretas).

Observación. Todos los archivos necesarios para reproducir los resultados mostrados en este capítulo, junto con el fuente original de esta tesis en Markdown y los archivos de metadata necesarios para compilar a PDF y/o HTML a través de LaTeX, están disponibles en https://github.com/gtheler/thesis bajo licencia CC-BY. Todas las herramientas utilizadas, incluyendo el sistema operativo, el mallador, el propio solver FeenoX, los post-procesadores, los graficadores, los generadores de documentación (y todas las bibliotecas de las cuales todo este software depende) son libres y/o de código abierto.

Observación. Las mallas de los problemas resueltos en este capítulo (incluso la malla uniforme del caso i de la Sección 5.6) han sido generadas con la herramienta de mallado Gmsh [7] y las vistas de post-procesamiento han sido creadas con la herramienta ParaView [1]. Ambas son libres, abiertas y amenas a la simulación programática.

5.1 Mapeo en mallas no conformes

TL;DR: Sobre la importancia de que FeenoX siga la filosofía Unix.

Este primer caso no resuelve ninguna PDE pero sirve para ilustrar…

las ideas de la filosofía Unix [17], [19], en particular programas que…
- hagan una cosa y que la hagan bien
- trabajen juntos
- manejen flujos¹ de texto porque esa es una interfaz universal.
la capacidad de FeenoX de leer distribuciones espaciales definidas sobre los nodos de una cierta malla no estructurada y de evaluarla en posiciones \mathbf{x} arbitrarias.

Una aplicación de esta segunda característica es leer una distribución espacial de temperaturas calculadas por un solver térmico (el mismo FeenoX podría servir) y utilizarlas para construir la matriz de rigidez de otro problema (por ejemplo elasticidad lineal para problemas termo-mecánicos o transporte o difusión de neutrones para neutrónica realimentada con termohidráulica). En este caso, los puntos de evaluación son los puntos de Gauss de los elementos de la segunda malla.

En este problema comenzamos escribiendo una función f(x,y,z) definida algebráicamente en los nodos de un cubo unitario [0,1]\times[0,1]\times[0,1] creado en Gmsh con la instrucción Box que llama a la primitiva apropiada del núcleo² OpenCASCADE:

SetFactory("OpenCASCADE");
Box(1) = {0, 0, 0, 1, 1, 1};

Realizamos el mallado con un algoritmo completamente no estructurado utilizando una cierta cantidad n_1 de elementos por lado. Luego, leemos esa malla de densidad c_1 con los valores nodales de f(\mathbf{x}) y los interpolamos en la posición de los nodos del mismo cubo mallado con otra densidad n_2. Como hemos partido de una función algebraica, podemos evaluar el error cometido en la interpolación en función de las densidades n_1 y n_2.

Observación. Este procedimiento no es exactamente el necesario para realizar cálculos acoplados ya que la evaluación en la segunda malla es sobre los nodos y no sobre los puntos de Gauss, pero el concepto es el mismo: interpolar valores nodales en puntos arbitrarios.

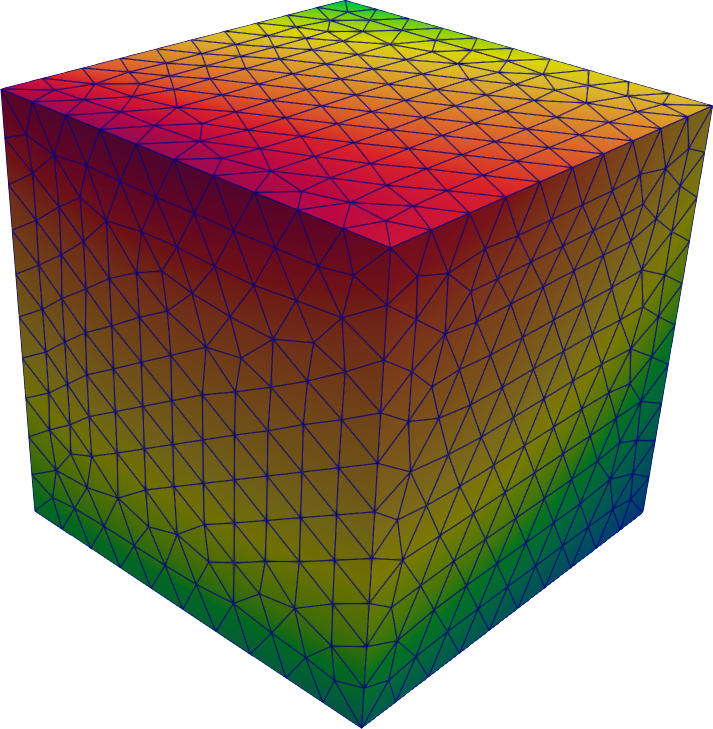
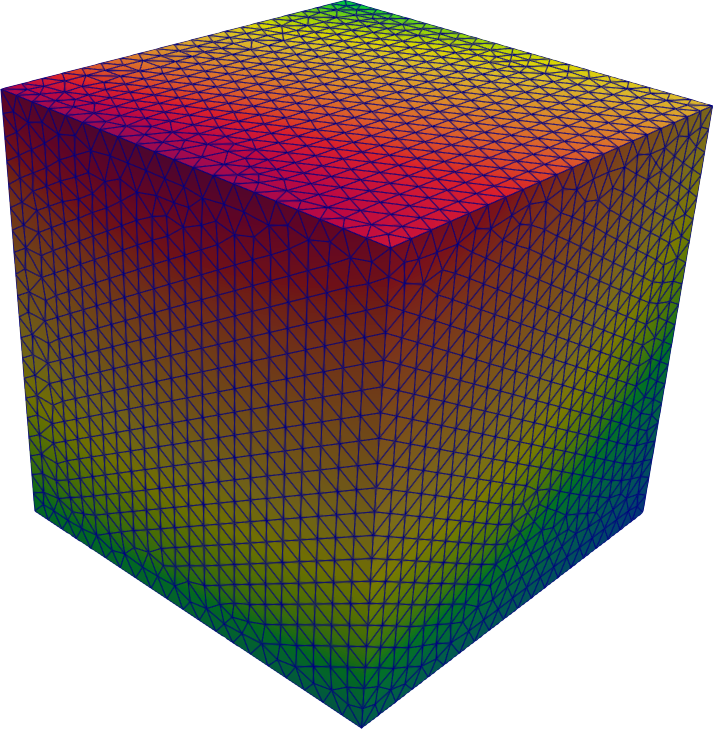
El script run.sh realiza una inicialización (0) y tres pasos (1–3):

Lee como un string el primer argumento $1 en la línea de comandos después del archivo de entrada³ la función f(x,y,z). Si no se provee ningún argumento, utiliza como default

f(x,y,z) = 1 + x \cdot \sqrt{y} + 2 \cdot \log(1+y+z) + \cos(x z) \cdot e^{y \cdot z}
Llama a Gmsh con el archivo de entrada cube.geo para crear cinco mallas con n=10, 20, 30, 40, 50 elementos por lado a partir del cubo base con diferentes valores del parámetro -clscale:
```
SetFactory("OpenCASCADE");
Box(1) = {0, 0, 0, 1, 1, 1};
```
Cada una de estas cinco mallas cube-n.msh (donde n es 10, 20, 30, 40 o 50) es leída por FeenoX y se crea un archivo nuevo llamado cube-n-src.msh con un campo escalar f definido sobre los nodos según el argumento pasado por run.sh a FeenoX en $1 (figura 5.1):
```
READ_MESH cube-$2.msh
f(x,y,z) = $1
WRITE_MESH cube-$2-src.msh f
```
Para cada combinación n_1=10,\dots,50 y n_2=10,\dots,50, lee la malla cube-n1-src.msh con el campo escalar f y define una función f(x,y,z) definida por puntos en los nodos de la malla de entrada. Entonces escribe un archivo de salida VTK llamado cube-n1-n2-dst.vtk con dos campos escalares nodales sobre la malla de salida cube-$3.msh:
1. la función f(x,y,z) de la malla de entrada interpolada en la malla de salida
2. el valor absoluto de la diferencia entre la f(x,y,z) interpolada y la expresión algebraica original de referencia:
```
READ_MESH cube-$2-src.msh DIM 3 READ_FUNCTION f
READ_MESH cube-$3.msh
WRITE_MESH cube-$2-$3-dst.vtk f NAME error "abs(f(x,y,z)-($1))" MESH cube-$3.msh
```
Finalmente, para cada archivo VTK, lee el campo escalar como f_msh y calcula el error L_2 como

e_2 = \bigintss \sqrt{ \Big[f_\text{msh}(\mathbf{x}) - f(\mathbf{x})\Big]^2} \, d^3\mathbf{x}

y el error L_\infty como

e_\infty = \max \Big| f_\text{msh}(\mathbf{x}) - f(\mathbf{x})\Big|

e imprime una línea con un formato adecuado para que el script run.sh pueda escribir una tabla Markdown que pueda ser incluida en un archivo de documentación con control de versiones Git, tal como esta tesis de doctorado.
```
READ_MESH cube-$2-src.msh DIM 3 READ_FUNCTION f
READ_MESH cube-$3.msh
WRITE_MESH cube-$2-$3-dst.vtk f NAME error "abs(f(x,y,z)-($1))" MESH cube-$3.msh
```

La tabla 5.1 muestra el tiempo necesario para generar lo datos. La tabla 5.2 muestra los errores y el tiempo necesario para interpolar los datos.

(a)
n	elementos	nodos	tiempo de mallado [s]	tiempo de rellenado [s]
10	4.979	1.201	0,09	0,01
20	37.089	7.411	0,41	0,05
30	123.264	22.992	1,19	0,26
40	289.824	51.898	3,23	0,87
50	560.473	98.243	7,04	1,85

Tabla 5.1: Tiempo necesario para generar los datos.

(a)
n_1	n_2	error L_2	error L_\infty	tiempo [s]
10	10	1.3 \times 10^{-2}	6.2 \times 10^{-6}	0.02
10	20	1.3 \times 10^{-2}	9.0 \times 10^{-2}	0.08
10	30	1.3 \times 10^{-2}	9.6 \times 10^{-2}	0.32
10	40	1.3 \times 10^{-2}	9.4 \times 10^{-2}	1.01
10	50	1.3 \times 10^{-2}	9.8 \times 10^{-2}	1.94
20	10	1.3 \times 10^{-2}	4.1 \times 10^{-3}	0.06
20	20	6.2 \times 10^{-3}	6.9 \times 10^{-6}	0.11
20	30	6.4 \times 10^{-3}	6.4 \times 10^{-2}	0.40
20	40	6.2 \times 10^{-3}	6.7 \times 10^{-2}	0.98
20	50	6.1 \times 10^{-3}	6.7 \times 10^{-2}	2.30
30	10	1.3 \times 10^{-2}	1.7 \times 10^{-3}	0.29
30	20	6.4 \times 10^{-3}	6.4 \times 10^{-3}	0.36
30	30	4.2 \times 10^{-3}	7.1 \times 10^{-6}	0.57
30	40	4.3 \times 10^{-3}	4.7 \times 10^{-2}	1.48
30	50	4.2 \times 10^{-3}	5.3 \times 10^{-2}	2.78
40	10	1.3 \times 10^{-2}	1.2 \times 10^{-3}	0.99
40	20	6.3 \times 10^{-3}	5.3 \times 10^{-3}	1.06
40	30	4.3 \times 10^{-3}	1.3 \times 10^{-2}	1.44
40	40	3.1 \times 10^{-3}	7.4 \times 10^{-6}	1.95
40	50	3.2 \times 10^{-3}	3.6 \times 10^{-2}	3.79
50	10	1.3 \times 10^{-2}	6.0 \times 10^{-4}	2.07
50	20	6.2 \times 10^{-3}	2.1 \times 10^{-3}	2.31
50	30	4.2 \times 10^{-3}	3.9 \times 10^{-3}	2.62
50	40	3.2 \times 10^{-3}	2.4 \times 10^{-2}	3.74
50	50	2.5 \times 10^{-3}	7.3 \times 10^{-6}	4.26

Tabla 5.2: Errores y tiempos necesarios para interpolar los datos.

Observación. El cálculo del error L_\infty se hace sobre los nodos y sobre los puntos de Gauss. Recordar la figura 4.3.

Observación. Si f(\mathbf{x}) fuese lineal o incluso polinómica, los errores serían mucho menores.

Para finalizar este primer caso, las tablas 5.3 (a) y 5.3 (b) muestran los errores y los tiempos necesarios para realizar el mismo mapeo entre FeenoX y una biblioteca que forma parte de una solución comercial⁴ vendida por unas de las empresas de software de elementos finitos con mayor participación el el mercado mundial.

(a) De n_1 = 50 (98.243 nodos) a n_2 = 100 (nodos 741.243 nodos)
	Otro	FeenoX
Tiempo	33.4 seg	7.24 seg
Error L_2	2.859 \times 10^{-5}	2.901 \times 10^{-5}
Dif. más negativa	-2.509 \times 10^{-4}	-5.544 \times 10^{-3}
Dif. más positiva	+1.477 \times 10^{-4}	+7.412 \times 10^{-4}

(b) De n_1 = 100 (741.243 nodos) a n_2 = 50 (98.243 nodos)
	Otro	FeenoX
Tiempo	54.2 seg	1.63 seg
Error L_2	6.937 \times 10^{-6}	6.797 \times 10^{-6}
Dif. más negativa	-6.504 \times 10^{-5}	-5.164 \times 10^{-5}
Dif. más positiva	+2.605 \times 10^{-5}	+3.196 \times 10^{-5}

Tabla 5.3: Comparación de tiempos de mapeo entre FeenoX y otra alternativa

En el repositorio https://github.com/gtheler/feenox-non-conformal-mesh-interpolation se pueden encontrar más detalles sobre el análisis del mapeo no conforme propuesto por FeenoX.

5.2 El problema de Reed

TL;DR: Este problema tiene más curiosidad histórica que numérica. Es uno de los problemas más sencillos no triviales que podemos encontrar y sirve para mostrar que para tener en cuenta regiones vacías no se puede utilizar una formulación de difusión.

Este caso, que data de 1971 [18], es de los más sencillos que FeenoX puede resolver. Por lo tanto, por base de diseño, el archivo de entrada también debe ser sencillo. Aprovechamos, entonces, la sencillez de este primer problema para explicar en detalle cómo generar la malla con Gmsh y cómo preparar este archivo de entrada en forma apropiada.

El problema de Reed consiste en una geometría tipo slab adimensional para 0 < x < 8 con cinco zonas, cada una con secciones eficaces macroscópicas adimensionales uniformes (figura 5.2):

0 < x < 2 \mapsto Source 1
2 < x < 3 \mapsto Absorber
3 < x < 5 \mapsto Vacuum
5 < x < 6 \mapsto Source 2
6 < x < 8 \mapsto Reflector

Las fuentes de neutrones son independientes y no hay materiales físiles (ni fisionables), por lo que el problema a resolver es un sistema lineal de ecuaciones (KSP) y no un problema de autovalores (EPS)
El material “vacuum´” tiene secciones eficaces nulas, lo que implica que no puede utilizarse la aproximación de difusión ya que el coeficiente D(x) estaría mal definido.
Se espera que haya gradientes espaciales grandes en las interfaces entre materiales, por lo que vamos a refinar localizadamente alrededor de los puntos x=2, x=3, x=5 y x=6.
Como mencionamos en la definición 3.26, la ecuación de transporte es hiperbólica y necesita un término de estabilización en el término convectivo. FeenoX implementa un método tipo SUPG (definición 3.26) controlado por un factor \alpha que puede ser definido explícitamente en el archivo de entrada a través de la variable especial sn_alpha. Por defecto, \alpha = 1/2.
La condición de contorno en x=0 es tipo simetría, lo que implica que FeenoX utilice el método de penalidad para implementarla. Es posible elegir el peso en el archivo de entrada con la variable especial penalty_weight. Valores altos implican mayor precisión en la condición de contorno pero peor condicionamiento de la matriz global de rigidez \mat{K}.
La condición de contorno en x=8 es vacío, lo que corresponde a una condición de Dirichlet para las direcciones entrantes.

Podemos generar la geometría y la malla del problema reed.msh (que luego será leída por FeenoX) con el siguiente archivo de entrada de Gmsh:

//
//     |         |    |         |    |         |
//  m  | src= 50 | 0  |    0    | 1  |    0    |    v
//  i  |         |    |         |    |         |    a
//  r  | tot= 50 | 5  |    0    | 1  |    1    |    c
//  r  |         |    |         |    |         |    u
//  o  | scat=0  | 0  |    0    | 0.9|   0.9   |    u
//  r  |         |    |         |    |         |    m
//     |         |    |         |    |         |
//     |    1    | 2  |    3    | 4  |    5    |
//     |         |    |         |    |         |
//     +---------+----+---------+----+---------+-------> x
//    x=0       x=2  x=3       x=5  x=6       x=8   

lc0 = 0.25;   // tamaño de elemento base
f = 0.1;      // factor de refinamiento

// puntos en extremos de interfaces
Point(1) = {0, 0, 0, lc0};
Point(2) = {2, 0, 0, f*lc0};
Point(3) = {3, 0, 0, f*lc0};
Point(4) = {5, 0, 0, f*lc0};
Point(5) = {6, 0, 0, f*lc0};
Point(6) = {8, 0, 0, lc0};

// puntos medios de cada zona
Point(11) = {1,   0, 0, lc0};
Point(12) = {2.5, 0, 0, lc0};
Point(13) = {4,   0, 0, lc0};
Point(14) = {5.5, 0, 0, lc0};
Point(15) = {7,   0, 0, lc0};

// líneas geométricas
Line(1) = {1, 11};
Line(11) = {11, 2};
Line(2) = {2, 12};
Line(12) = {12, 3};
Line(3) = {3, 13};
Line(13) = {13, 4};
Line(4) = {4, 14};
Line(14) = {14, 5};
Line(5) = {5, 15};
Line(15) = {15, 6};

// líneas físicas
Physical Line("source1")   = {1,11};
Physical Line("absorber")  = {2,12};
Physical Line("void")      = {3,13};
Physical Line("source2")   = {4,14};
Physical Line("reflector") = {5,15};

// puntos físicos
Physical Point("left")  = {1};
Physical Point("right") = {6};

lo que da lugar a 81 nodos distribuidos heterogéneamente como ilustramos en la figura 5.3.

Figura 5.3: 81 nodos y 80 elementos tipo línea para el problema de Reed.

Estamos entonces en condiciones de preparar el archivo de entrada para FeenoX:

# ordenadas discretas en una dimensión a un grupo de energías
# leer N de la línea de comandos
PROBLEM neutron_sn DIM 1 GROUPS 1 SN $1

# leer la malla de este archivo
READ_MESH reed.msh
 
# propiedades de materiales (todas uniformes por zona)
MATERIAL source1       S1=50 Sigma_t1=50 Sigma_s1.1=0
MATERIAL absorber      S1=0  Sigma_t1=5  Sigma_s1.1=0
MATERIAL void          S1=0  Sigma_t1=0  Sigma_s1.1=0
MATERIAL source2       S1=1  Sigma_t1=1  Sigma_s1.1=0.9
MATERIAL reflector     S1=0  Sigma_t1=1  Sigma_s1.1=0.9

# condiciones de contorno
BC left  mirror
BC right vacuum

# resolver el problema = construir matrices y resolver el sistema
SOLVE_PROBLEM

# escribir la funcion phi1(x) en dos columnas ASCII
PRINT_FUNCTION phi1

Este (sencillo) archivo de entrada tiene 6 secciones bien definidas:

Definición (PROBLEM es un sustantivo) de
1. el tipo de PDE a resolver (neutron_sn)
2. la dimensión del dominio (DIM 1)
3. la cantidad de grupos de energía (GROUPS 1)
4. el orden N en S_N (SN $1) a leer como el primer argumento en la línea de comando de invocación del ejecutable feenox luego del archivo de entrada reed.fee.
Instrucción para leer la malla (READ_MESH es un verbo seguido de un sustantivo).
Definición de los nombres y propiedades de los materiales (MATERIAL es un sustantivo). Si los nombres de los materiales en el archivo de entrada de FeenoX coinciden con el nombre de las entidades físicas cuya dimensión es la del problema (líneas físicas en este caso unidimensional) entonces éstas se asocian implícitamente a los materiales. En cualquier caso, se puede hacer una asociación explícita con tantas palabras clave LABEL como sea necesario para cada material.
Definición de condiciones de contorno (BC es sigla de boundary condition que es un sustantivo adjetivado). De la misma manera, si el nombre de la condición de contorno coincide con el nombre de entidades físicas de dimensión menor a la dimensión del problema en la malla, la asociación se hace implícitamente. En forma similar, se pueden agregar palabras clave LABEL.
Instrucción para indicar que FeenoX debe resolver el problema (SOLVE_PROBLEM es un verbo). En este caso sencillo esta instrucción debe venir luego de leer la malla y antes de escribir el resultado. En casos ligeramente más complejos como estudiamos a continuación donde cambiamos los valores por defecto de las variables sn_alpha y penalty_weight, la instrucción SOLVE_PROBLEM debe venir luego de estas instrucciones de asignación.
Instrucción para escribir en la salida estándar una columna con la posición de los nodos (en este caso un único valor para x) y el flujo escalar \phi evaluado en x. Podríamos haber pedido los flujos angulares \psi_{mg} a continuación para obtener más columnas de datos, pero dado que el parámetro N se lee desde la línea de comandos no podemos saber al momento de preparar el archivo de entrada cuántos flujos angulares van a estar definidos. Por ejemplo, si $1 es 2 entonces psi1.1 y psi1.2 están definidas pero psi1.3 no lo estará por lo que la línea
```
PRINT_FUNCTION psi1 psi1.1 psi1.2 psi1.3 psi1.4
```
dará un error de parseo si $1 es 2 (pero funcionará bien si $1 es 4 ). En problemas multidimensionales, la instrucción WRITE_RESULTS se hará cargo del problema porque escribirá automáticamente en el archivo de salida (en formato Gmsh o VTK) la cantidad correcta de flujos angulares definidos. Otra forma de tener como salida los flujos angulares es reemplazar la instrucción PRINT_FUNCTION por
```
INCLUDE print-$1.fee
```
y preparar diferentes archivos print-2.fee, print-4.fee, print-6.fee, etc. cada uno conteniendo la instrucción PRINT_FUNCTION con la cantidad apropiada de argumentos para cada N.

La ejecución propiamente dicha de este problema involucra entonces invocar a Gmsh para generar la malla reed.msh a partir de reed.geo y luego invocar a FeenoX con el archivo de entrada reed.fee y el valor de N deseado a continuación. Como queremos construir un gráfico con el perfil de flujo escalar, redireccionamos cada una de las salidas estándar de las diferentes ejecuciones de FeenoX a diferentes archivos ASCII:

$ gmsh -1 reed.geo
Info    : Running 'gmsh -1 reed.geo' [Gmsh 4.12.0-git-01ed7170f, 1 node, max. 1 thread]
Info    : Started on Thu Oct 19 19:31:42 2023
Info    : Reading 'reed.geo'...
Info    : Done reading 'reed.geo'
Info    : Meshing 1D...
Info    : [  0%] Meshing curve 1 (Line)
Info    : [ 10%] Meshing curve 2 (Line)
Info    : [ 20%] Meshing curve 3 (Line)
Info    : [ 30%] Meshing curve 4 (Line)
Info    : [ 40%] Meshing curve 5 (Line)
Info    : [ 50%] Meshing curve 11 (Line)
Info    : [ 60%] Meshing curve 12 (Line)
Info    : [ 70%] Meshing curve 13 (Line)
Info    : [ 80%] Meshing curve 14 (Line)
Info    : [ 90%] Meshing curve 15 (Line)
Info    : Done meshing 1D (Wall 0.0142831s, CPU 0.010774s)
Info    : 81 nodes 91 elements
Info    : Writing 'reed.msh'...
Info    : Done writing 'reed.msh'
Info    : Stopped on Thu Oct 19 19:31:42 2023 (From start: Wall 0.0161955s, CPU 0.010992s)
$ feenox reed.fee 2 > reed-s2.csv
$ feenox reed.fee 4 > reed-s4.csv
$ feenox reed.fee 8 > reed-s8.csv

Podemos darle una vuelta de tuerca más a la filosofía Unix y reemplazar las últimas tres llamadas explícitas a feenox por un bucle de Bash. Incluso aprovechamos para ordenar las líneas en orden creciente según la primera columna para poder graficar “con líneas”:

$ for N in 2 4 8; do feenox reed.fee $N | sort -g > reed-s$N.csv; done
$

La figura 5.4 muestra el flujo escalar calculado por FeenoX y una comparación con resultados independientes obtenidos con una implementación de un solver 1D ad-hoc en una herramienta matemática privativa y publicados en un blog académico.⁵ Esta solución independiente utiliza una malla uniforme con la misma cantidad (81) de nodos que FeenoX.

Figura 5.4: Perfil de flujo angular \phi(x) para el problema de Reed

5.2.1 Efecto del factor de estabilización

Estudiemos brevemente el efecto de modificar el factor de estabilización \alpha mediante la variable sn_alpha. Para ello generamos una malla un poco más gruesa con la opción -clscale de Gmsh y reducimos el número de nodos de 81 a 53:

$ gmsh -1 reed.geo -clscale 2 -o reed-coarse.msh
[...]
Info    : Done meshing 1D (Wall 0.0160784s, CPU 0.011781s)
Info    : 53 nodes 63 elements
Info    : Writing 'reed-coarse.msh'...
Info    : Done writing 'reed-coarse.msh'
Info    : Stopped on Thu Oct 19 20:20:01 2023 (From start: Wall 0.019359s, CPU 0.015746s)
$

Agregamos entonces la posibilidad de leer otro argumento en la línea de comandos $2 y lo asignamos a dicha variable antes de pedir la instrucción SOLVE_PROBLEM. Además ahora le pedimos directamente a FeenoX que escriba la función \phi_1(x) en un archivo de texto cuyo nombre es $0-$1-$2.csv donde $0 es el nombre del archivo de entrada sin la extensión .fee:

PROBLEM neutron_sn DIM 1 GROUPS 1 SN $1
READ_MESH reed-coarse.msh
MATERIAL source1       S1=50 Sigma_t1=50 Sigma_s1.1=0
MATERIAL absorber      S1=0  Sigma_t1=5  Sigma_s1.1=0
MATERIAL void          S1=0  Sigma_t1=0  Sigma_s1.1=0
MATERIAL source2       S1=1  Sigma_t1=1  Sigma_s1.1=0.9
MATERIAL reflector     S1=0  Sigma_t1=1  Sigma_s1.1=0.9
BC left  mirror
BC right vacuum

sn_alpha = $2

SOLVE_PROBLEM
PRINT_FUNCTION phi1 FILE $0-$1-$2.csv

Con dos bucles de Bash anidados probamos todas las combinaciones posibles de N=2,4,8 y \alpha = 0.01,0.25,1:

$ for N in 2 4 8; do for alpha in 0.01 0.25 1; do feenox reed-alpha.fee $N $alpha ; done; done
$ for N in 2 4 8; do for alpha in 0.01 0.25 1; do sort -g reed-alpha-$N-$alpha.csv > reed-alpha-$N-$alpha-sorted.csv; done; done

para obtener la figura 5.5.

Observación. Como veremos más adelante (por ejemplo en la Sección 5.9 o en la Sección 5.4), el realizar estudios paramétricos sobre más de un parámetro la cantidad de resultados a analizar aumenta geométricamente. Debido a que FeenoX permite la flexibilidad de ser ejecutado en bucles y de pasar parámetros por líneas de comando, la generación de los resultados es extremadamente eficiente, lo que hace que sea relativamente mucho más difícil el análisis de dichos resultados que la generación de los datos en sí. Esto pone en relieve la importancia de la regla de economía de Unix: no sólo el costo relativo de la unidad de tiempo de CPU es al menos tres órdenes de magnitud menor al costo de la unidad de tiempo de un ingeniero sino que también el tiempo absoluto necesario para analizar resultados es mayor que para generarlos.

5.2.2 Efecto del orden de los elementos

Para finalizar el estudio de este primer problema neutrónico sencillo volvemos a resolver el mismo caso pero utilizando elementos de segundo orden. Está claro que para poder comparar soluciones debemos tener en cuenta el esfuerzo computacional que cada método necesita. Para el mismo tamaño de elemento, el tamaño del problema para una malla de segundo orden es mucho más grande que para una malla de primer orden. Por lo tanto, lo primero que hay que hacer es

refinar la malla de primer orden, o
hacer más gruesa la malla de segundo orden.

Por otro lado el patrón de la matriz también aumenta (el ancho de banda es mayor en la malla de segundo orden) por lo que también cambia el esfuerzo necesario no sólo para construir la matriz sino también para invertirla, especialmente en términos de memoria. En algunos tipos de problemas (como por ejemplo elasticidad ver Sección B.2.2.2), está probado que cualquier esfuerzo necesario para resolver un problema con elementos de segundo orden vale la pena ya que los elementos de primer orden—aún cuando la malla esté muy refinada—padecen del efecto numérico conocido como shear locking que arroja resultados poco precisos. Pero en el caso de transporte (e incluso difusión) de neutrones no está claro que, para el mismo tamaño de problema, la utilización de elementos de alto orden sea más precisa que la de elementos de primer orden, más allá de la posibilidad de representar geometrías curvas con más precisión.

De cualquier manera, presentamos entonces resultados para el problema de Reed con elementos unidimensionales de segundo orden. Primeramente le pedimos a Gmsh que nos prepare una malla más gruesa aún que la anterior, pero de orden dos. Esto da 53 nodos, tal como la malla reed-coarse.msh de la sección anterior:

$ gmsh -1 reed.geo -order 2 -clscale 5 -o reed-coarser2.msh
[...]
Info    : Done meshing order 2 (Wall 0.000161366s, CPU 9.7e-05s)
Info    : 53 nodes 37 elements
Info    : Writing 'reed-coarser2.msh'...
Info    : Done writing 'reed-coarser2.msh'
Info    : Stopped on Fri Oct 20 13:45:05 2023 (From start: Wall 0.0102896s, CPU 0.012253s)
$

Ahora preparamos este archivo de entrada que

utiliza esta malla de segundo orden,
resuelve el problema de Reed
lee el flujo obtenido en la sección anterior para \alpha=1, y
escribe la diferencia algebraica entre los dos flujos escalares en función de x con un paso espacial \Delta x=10^{-3}

para obtener la figura 5.6.

PROBLEM neutron_sn DIM 1 GROUPS 1 SN $1
READ_MESH reed-coarser2.msh
MATERIAL source1       S1=50 Sigma_t1=50 Sigma_s1.1=0
MATERIAL absorber      S1=0  Sigma_t1=5  Sigma_s1.1=0
MATERIAL void          S1=0  Sigma_t1=0  Sigma_s1.1=0
MATERIAL source2       S1=1  Sigma_t1=1  Sigma_s1.1=0.9
MATERIAL reflector     S1=0  Sigma_t1=1  Sigma_s1.1=0.9
BC left  mirror
BC right vacuum
sn_alpha = 1
SOLVE_PROBLEM

# leemos la solución de primer orden para comparar
FUNCTION phi_first(x) FILE reed-alpha-$1-1-sorted.csv

# escribimos el flujo y la diferencia
PRINT_FUNCTION phi1 phi_first(x)-phi1(x) MIN 0 MAX 8 STEP 1e-3 FILE $0-$1.csv

Observación. No hay una definición o instrucción específica que le indique a FeenoX el orden de los elementos a usar. El solver lee la malla con la instrucción READ_MESH y emplea los elementos allí definidos, que pueden ser de primero o segundo orden. En los casos anteriores, los elementos de mayor orden eran líneas de dos nodos (a.k.a. line2). En este caso, son líneas de tres nodos (a.k.a. line3).

$ for N in 2 4 8; do feenox reed2.fee $N; done
$

Figura 5.6: Diferencia entre flujos de primer y segundo orden en el problema de Reed

Observación. Dado que las propiedades de los materiales y las condiciones de contorno fueron siempre iguales para todos los casos resueltos en esta sección, una gestión más eficiente de los archivos de entrada habría implicado que creáramos un archivo separado con las palabras clave MATERIAL y BC para luego incluir dicho archivo desde cada uno de los archivos de entrada con la palabra clave INCLUDE (por ejemplo en la Sección 5.10). Como este es el primer problema neutrónico resuelto con FeenoX en esta tesis, hemos elegido dejar explícitamente la definición de materiales y de condiciones de contorno. En secciones siguientes vamos a utilizar la palabra clave INCLUDE, que es para lo que fue diseñada.

5.3 IAEA PWR Benchmark

TL;DR: El problema original de 1976 propone resolver un cuarto de núcleo cuando en realidad la simetría es 1/8.

Este problema fue propuesto por Argonne National Laboratory [2] y luego adoptado por la IAEA como un benchmark estándar para validar códigos de difusión. Está compuesto

por un problema 2D que representa un cuarto de una geometría típica de PWR sobre el plano x-y más un buckling geométrico para tener en cuenta las pérdidas en la dirección z, y
un problema completamente tridimensional de un cuarto de núcleo

5.3.1 Caso 2D original

La figura 5.7, preparada en su momento para la publicación [26], muestra la geometría del problema. La tabla 5.4 muestra las secciones eficaces macroscópicas a dos grupos de cada zona. El problema pide calcular varios puntos, incluyendo

el factor de multiplicación efectivo k_\text{eff}
perfiles de flujo a lo largo de la diagonal
valores y ubicación de flujos máximos
potencias medias en cada canal

Figura 5.7: Caso 2D original del benchmark PWR de IAEA

(a) Datos originales de [2] {#tbl-iaea-xs2}. El material 5 es utilizado sólo en el caso 3D.
Región	D_1	D_2	\Sigma_{s1 \rightarrow 2}	\Sigma_{a1}	\Sigma_{a2}	\nu\Sigma_{f2}	Material
1	1.5	0.4	0.02	0.01	0.08	0.135	Fuel 1
2	1.5	0.4	0.02	0.01	0.085	0.135	Fuel 2
3	1.5	0.4	0.02	0.01	0.13	0.135	Fuel 2 + Rod
4	2.0	0.3	0.04	0	0.01	0	Reflector
5	2.0	0.3	0.04	0	0.055	0	Refl. + Rod

Tabla 5.4: Secciones eficaces macroscópicas (uniformes por zonas) del benchmark PWR de IAEA. Al caso 2D se le debe sumar un término de buckling geométrico B_g^2=0.8 \times 10^{-4}.

En la referencia [26] hemos resuelto completamente el problema utilizando la segunda versión de la implementación (denominada milonga), incluso utilizando triángulos y cuadrángulos, diferentes algoritmos y densidades de mallado, etc. Más aún, esa versión era capaz de resolver la ecuación de difusión tanto con elementos como con volúmenes finitos tal como explicamos en la monografía [25], donde también resolvemos el problema. En la presentación [32] mostramos cómo habíamos resuelto el benchmark con la primera versión del código.

En esta sección calculamos solamente el factor de multiplicación y la distribución espacial de flujos. En este caso vamos a prestar más atención al archivo de entrada de FeenoX que a la generación de la malla, que para este caso puede ser estructurada como mostramos en la figura 5.8.

Figura 5.8: Malla para el caso 2D original con simetría 1/4

PROBLEM neutron_diffusion 2D GROUPS 2

DEFAULT_ARGUMENT_VALUE 1 quarter   # quarter o eighth
READ_MESH iaea-2dpwr-$1.msh

Bg2 = 0.8e-4  # buckling geometrico en la dirección z
MATERIAL fuel1 {
  D1=1.5    Sigma_a1=0.010+D1(x,y)*Bg2    Sigma_s1.2=0.02
  D2=0.4    Sigma_a2=0.080+D2(x,y)*Bg2    nuSigma_f2=0.135   }

MATERIAL fuel2 {
  D1=1.5    Sigma_a1=0.010+D1(x,y)*Bg2    Sigma_s1.2=0.02
  D2=0.4    Sigma_a2=0.085+D2(x,y)*Bg2    nuSigma_f2=0.135   }

MATERIAL fuel2rod {
  D1=1.5    Sigma_a1=0.010+D1(x,y)*Bg2    Sigma_s1.2=0.02
  D2=0.4    Sigma_a2=0.130+D2(x,y)*Bg2    nuSigma_f2=0.135   }

MATERIAL reflector {
  D1=2.0    Sigma_a1=0.000+D1(x,y)*Bg2    Sigma_s1.2=0.04
  D2=0.3    Sigma_a2=0.010+D2(x,y)*Bg2 }
  
BC external vacuum=0.4692
BC mirror   mirror

SOLVE_PROBLEM

PRINT      "grados de libertad = " total_dofs
PRINT %.5f "keff = " keff
WRITE_RESULTS FORMAT vtk

Observación. Hay una relación bi-unívoca bastante clara entre la definición del problema en el reporte [2] y el archivo de entrada necesario para resolverlo con FeenoX. El lector experimentado podrá notar que esta característica (que es parte de la base de diseño del software) no es común en otros solvers, ni neutrónicos ni termo-mecánicos.

Observación. Si bien las secciones eficaces son uniformes, la sección eficaz de absorción está dada por una expresión que es la suma de la sección eficaz base más el producto del coeficiente de difusión D_g por el buckling geométrico B_g. En lugar de volver a escribir la constante numérica correspondiente al material, escribimos D_g(x,y) para que FeenoX reemplace el valor apropiado del coeficiente de difusión del material en cuestión por nosotros.

Observación. Tal como en el problema de Reed de la sección anterior donde teníamos elementos de tipo punto para definir condiciones de contorno, en este caso bi-dimensional la malla contiene elementos de dimensión uno (tipo líneas) donde se aplican las condiciones de contorno. Los elementos que discretizan las líneas x=0 e y=0 tienen asignado (en el archivo de entrada de Gmsh no mostrado) el nombre “vacuum” y los que discretizan el borde externo del reflector, el nombre “mirror”. Estos dos nombres son usados en las dos instrucciones BC del archivo de entrada de FeenoX para indicar qué clase de condición de contorno hay que aplicarle a cada grupo de elementos de dimensión topológica menor a la del problema.

$ gmsh -2 iaea-2dpwr-quarter.geo
[...]
Info    : Done meshing 2D (Wall 0.0422971s, CPU 0.042152s)
Info    : 1033 nodes 1286 elements
Info    : Writing 'iaea-2dpwr-quarter.msh'...
Info    : Done writing 'iaea-2dpwr-quarter.msh'
Info    : Stopped on Fri Oct 20 15:55:03 2023 (From start: Wall 0.0522626s, CPU 0.060603s)
$ time feenox iaea-2dpwr.fee
grados de libertad =    2066
keff =  1.02985

real    0m0.696s
user    0m0.090s
sys     0m0.162s
$

5.3.2 Caso 2D con simetría 1/8

Como deslizamos en el capítulo 1, bien mirado el problema no tiene simetría 1/4 sino simetría 1/8. Sucede que para poder explotar dicha simetría se necesita una malla no estructurada, que ni en 1976 ni en 2024 (excepto algunos casos puramente académicos como [4], [14], [15], [34]) es una característica de los solvers neutrónicos de nivel de núcleo. De hecho el paper [26] justamente ilustra el hecho de que las mallas no estructuradas permiten reducir la cantidad de grados de libertad necesarios para resolver un cierto problema.

Figura 5.9: Malla para el caso 2D original con simetría 1/8

Utilizando eighth como argumento $1 podemos usar el mismo archivo de entrada pero con la malla de la figura 5.9:

$ gmsh -2 iaea-2dpwr-eighth.geo
[...]
Info    : 668 nodes 1430 elements
Info    : Writing 'iaea-2dpwr-eighth.msh'...
Info    : Done writing 'iaea-2dpwr-eighth.msh'
Info    : Stopped on Fri Oct 20 17:58:06 2023 (From start: Wall 0.0331908s, CPU 0.040327s)
$ time feenox iaea-2dpwr.fee eighth
grados de libertad =    1336
keff =  1.02974

real    0m0.681s
user    0m0.075s
sys     0m0.161s
$

Figura 5.10: Flujos rápidos y térmicos en el problema 2D de IAEA con simetría 1/8 resuelto con difusión. La imagen del flujo rápido corresponde a una reflexión con respecto a una línea a 45 grados.

Observación. El tiempo de CPU reportado por time es el mismo independiente de la cantidad de grados de libertad. Esto indica que el tamaño del problema es muy pequeño y el tiempo necesario para construir las matrices y resolverlas es despreciable frente al overhead de cargar un ejecutable, inicializar bibliotecas compartidas, etc. Podemos verificar esta afirmación analizando la salida de la opción --log_view que le indica a PETSc que agregue una salida con datos de performance:

$ feenox iaea-2dpwr.fee eighth --log_view
grados de libertad =    1336
keff =  1.02974
[...]
Summary of Stages:   ----- Time ------  ----- Flop ------ 
                        Avg     %Total     Avg     %Total 
 0:      Main Stage: 2.0911e-03   7.7%  0.0000e+00   0.0% 
 1:            init: 2.1185e-04   0.8%  0.0000e+00   0.0% 
 2:           build: 9.7703e-03  36.1%  0.0000e+00   0.0% 
 3:           solve: 1.4487e-02  53.6%  1.9467e+07 100.0% 
 4:            post: 4.8677e-04   1.8%  0.0000e+00   0.0% 
[...]
$

En efecto, se necesitan menos de 10 milisegundos para construir las matrices del problema y menos de 15 para resolverlo.

5.3.3 Caso 2D con reflector circular

Mirando un poco más en detalle la geometría, hay un detalle que también puede ser considerado con mallas no estructuradas: la superficie exterior del reflector. En efecto, en una geometría tipo PWR cada uno de los canales proyecta un cuadrado en la sección transversal. Pero el reflector sigue la forma del recipiente de presión que es un cilindro (figura 5.11 (a)). Con FeenoX es posible resolver fácilmente esta geometría con el mismo archivo de entrada con la malla de la figura 5.11 (b) que incluye una mezcla de

zonas estructuradas y no estructuradas, y
triángulos y cuadrángulos.

$ gmsh -2 iaea-2dpwr-eighth-circular.geo
Info    : 524 nodes 680 elements
Info    : Writing 'iaea-2dpwr-eighth-circular.msh'...
Info    : Done writing 'iaea-2dpwr-eighth-circular.msh'
Info    : Stopped on Fri Oct 20 17:58:37 2023 (From start: Wall 0.0314288s, CPU 0.043231s)
$ time feenox iaea-2dpwr.fee eighth-circular
grados de libertad =    1048
keff =  1.02970

real    0m0.649s
user    0m0.048s
sys     0m0.156s
$

5.3.4 Caso 3D con simetría 1/8, reflector circular resuelto con difusión

Pasemos ahora al caso tri-dimensional. El problema original es una extensión sobre el eje z de la geometría con simetría 1/4 y reflector no circular. Como ya vimos en 2D, podemos tener simetría 1/8 y reflector cilíndrico. Ya que estamos en 3D, podemos preparar la geometría con una herramienta tipo CAD como es usual en análisis de ingeniería tipo CAE. En particular, usamos la plataforma CAD Onshape que corre en la nube y se utiliza directamente desde el navegador.⁶ La figura 5.12 muestra la geometría continua, que luego de ser mallada con Gmsh con elementos de segundo orden arroja la malla de la figura 5.13.

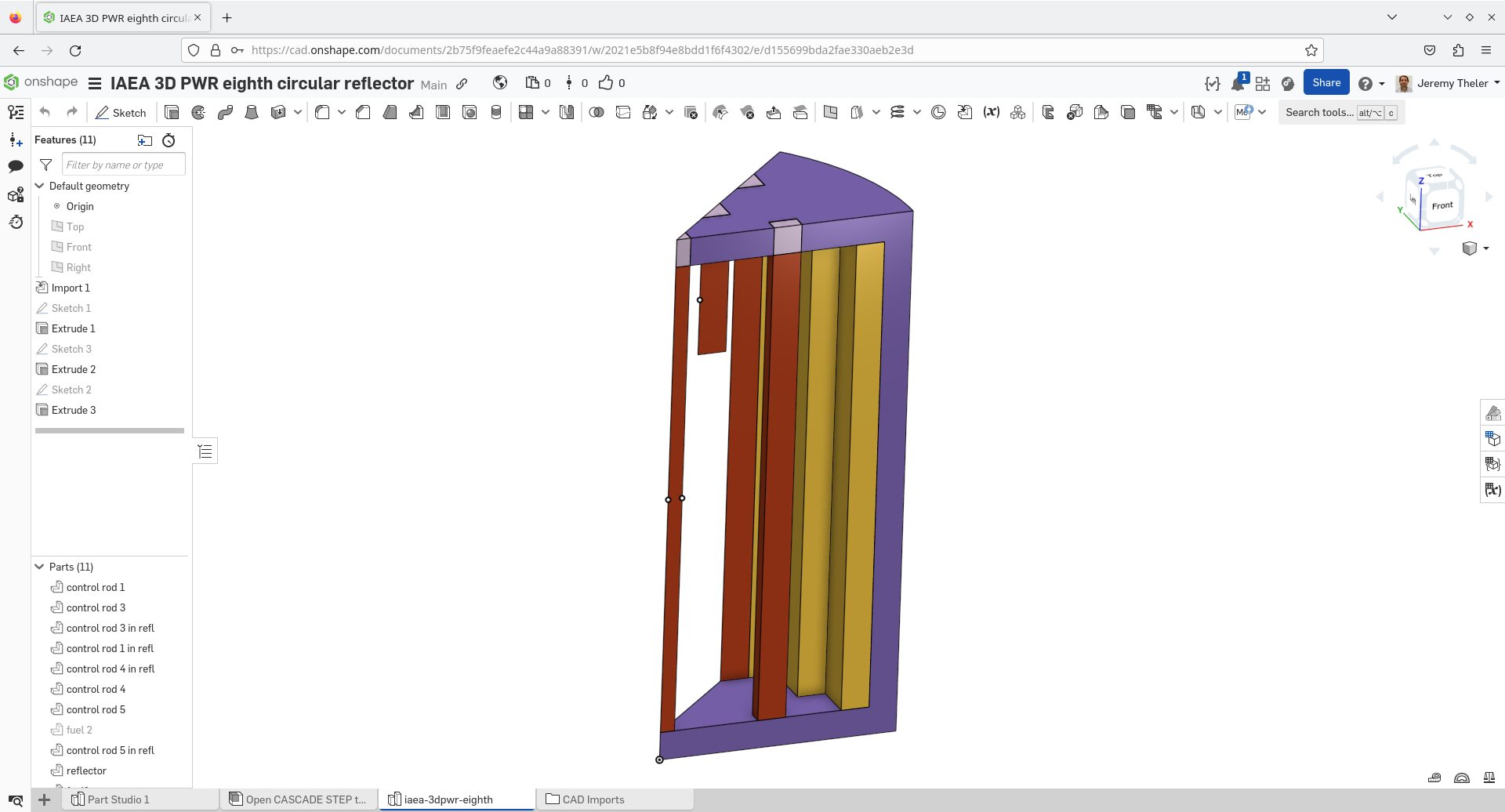
Figura 5.12: Preparación de la geometría del benchmark PWR 3D de IAEA en Onshape

El archivo de entrada sigue siendo relativamente sencillo, sólo que ahora agregamos un poco más de información a la salida:

PROBLEM neutron_diffusion 3D GROUPS 2

DEFAULT_ARGUMENT_VALUE 1 quarter
READ_MESH iaea-3dpwr-$1.msh

MATERIAL fuel1     D1=1.5 D2=0.4 Sigma_s1.2=0.02 Sigma_a1=0.01 Sigma_a2=0.08  nuSigma_f2=0.135
MATERIAL fuel2     D1=1.5 D2=0.4 Sigma_s1.2=0.02 Sigma_a1=0.01 Sigma_a2=0.085 nuSigma_f2=0.135
MATERIAL fuel2rod  D1=1.5 D2=0.4 Sigma_s1.2=0.02 Sigma_a1=0.01 Sigma_a2=0.13  nuSigma_f2=0.135
MATERIAL reflector D1=2.0 D2=0.3 Sigma_s1.2=0.04 Sigma_a1=0    Sigma_a2=0.01  nuSigma_f2=0
MATERIAL reflrod   D1=2.0 D2=0.3 Sigma_s1.2=0.04 Sigma_a1=0    Sigma_a2=0.055 nuSigma_f2=0
  
BC vacuum   vacuum=0.4692
BC mirror   mirror

SOLVE_PROBLEM
WRITE_RESULTS FORMAT vtk

PRINT  "geometry = $1"
PRINTF "    keff = %.5f"     keff
PRINTF "   nodes = %g"       nodes
PRINTF "    DOFs = %g"       total_dofs
PRINTF "  memory = %.1f Gb (local) %.1f Gb (global)" mpi_memory_local() mpi_memory_global()
PRINTF "    wall = %.1f sec" wall_time()

Como somos ingenieros y tenemos un trauma profesional con el tema de performance, debemos comparar la “ganancia” de usar simetría 1/8 con respecto al original de 1/4:

$ feenox iaea-3dpwr.fee quarter
geometry = quarter
    keff = 1.02918
   nodes = 70779
    DOFs = 141558
[0/1 tux]   memory = 2.3 Gb (local) 2.3 Gb (global)
    wall = 26.1 sec
$ feenox iaea-3dpwr.fee eighth
geometry = eighth
    keff = 1.02912
   nodes = 47798
    DOFs = 95596
[0/1 tux]   memory = 1.2 Gb (local) 1.2 Gb (global)
    wall = 12.7 sec
$ feenox iaea-3dpwr.fee eighth-circular
geometry = eighth-circular
    keff = 1.08307
   nodes = 32039
    DOFs = 64078
[0/1 tux]   memory = 0.8 Gb (local) 0.8 Gb (global)
    wall = 7.9 sec
$

La figura 5.14 muestra que ahora sí tenemos una ganancia significativa al reducir el tamaño del problema mediante la explotación de la simetría. El tiempo para construir la matriz pasó de 3.2 segundos a 2.0 (recordar que son elementos de segundo orden) y el tiempo necesario para resolver el problema bajó de 21 a 10 segundos.

Figura 5.14: Comparación entre la salida `--log_view` del caso 1/4 y 1/8 con el mismo reflector

Podemos investigar un poco qué sucede si quisiéramos resolver el problema en paralelo:

$ mpiexec -n 1 feenox iaea-3dpwr.fee quarter
geometry = quarter
    keff = 1.02918
   nodes = 70779
    DOFs = 141558
[0/1 tux]   memory = 2.3 Gb (local) 2.3 Gb (global)
    wall = 26.2 sec
$ mpiexec -n 2 feenox iaea-3dpwr.fee quarter
geometry = quarter
    keff = 1.02918
   nodes = 70779
    DOFs = 141558
[0/2 tux]   memory = 1.5 Gb (local) 3.0 Gb (global)
[1/2 tux]   memory = 1.5 Gb (local) 3.0 Gb (global)
    wall = 17.0 sec
$ mpiexec -n 4 feenox iaea-3dpwr.fee quarter
geometry = quarter
    keff = 1.02918
   nodes = 70779
    DOFs = 141558
[0/4 tux]   memory = 1.0 Gb (local) 3.9 Gb (global)
[1/4 tux]   memory = 0.9 Gb (local) 3.9 Gb (global)
[2/4 tux]   memory = 1.1 Gb (local) 3.9 Gb (global)
[3/4 tux]   memory = 0.9 Gb (local) 3.9 Gb (global)
    wall = 13.0 sec
$

5.3.5 Caso 3D con simetría 1/8, reflector circular resuelto con S_4

Para finalizar el caso, mostramos que FeenoX puede resolver no sólo este problema con el método de difusión sino también con ordenadas discretas. Este archivo de entrada calcula la distribución de flujos que ya hemos mostramos en la figura 1.2 del capítulo 1.

PROBLEM neutron_sn 3D GROUPS 2 SN 4 #PROGRESS
READ_MESH iaea-3dpwr-eighth-circular-s4.msh

MATERIAL fuel1     Sigma_s1.2=0.02 Sigma_a1=0.01 Sigma_a2=0.08  nuSigma_f2=0.135
MATERIAL fuel2     Sigma_s1.2=0.02 Sigma_a1=0.01 Sigma_a2=0.085 nuSigma_f2=0.135
MATERIAL fuel2rod  Sigma_s1.2=0.02 Sigma_a1=0.01 Sigma_a2=0.13  nuSigma_f2=0.135
MATERIAL reflector Sigma_s1.2=0.04 Sigma_a1=0    Sigma_a2=0.01  nuSigma_f2=0
MATERIAL reflrod   Sigma_s1.2=0.04 Sigma_a1=0    Sigma_a2=0.055 nuSigma_f2=0

BC vacuum   vacuum
BC mirror   mirror

PRINTF " nodes = %g"   nodes
PRINTF_ALL "solving..."
mumps_icntl_14 = 200
ksp_rtol = 1e-9
penalty_weight=100

SOLVE_PROBLEM
WRITE_RESULTS FORMAT vtk

# print results
PRINTF "  DOFs = %g"   total_dofs
PRINTF "  keff = %.5f" keff
PRINTF "  wall = %.1f sec" wall_time()

mem_global = mpi_memory_global()
mem_avg = mem_global / mpi_size
PRINTF "average memory = %.1f Gb" mem_avg
PRINTF " global memory = %.1f Gb" mem_global

$ feenox iaea-3dpwr-s4.fee --eps_monitor
 nodes = 3258
[0/1 tux] solving...
  1 EPS nconv=0 first unconverged value (error) 0.996623 (4.34362059e-05)
  2 EPS nconv=0 first unconverged value (error) 0.996626 (4.49580500e-08)
  3 EPS nconv=1 first unconverged value (error) 0.9353 (3.29379374e-08)
  DOFs = 156384
  keff = 0.99663
  wall = 197.9 sec
average memory = 13.6 Gb
 global memory = 13.6 Gb
$ mpiexec -n 4 feenox iaea-3dpwr-s4.fee --eps_monitor
 nodes = 3258
[0/4 tux] solving...
[1/4 tux] solving...
[2/4 tux] solving...
[3/4 tux] solving...
  1 EPS nconv=0 first unconverged value (error) 0.996625 (4.19395044e-05)
  2 EPS nconv=0 first unconverged value (error) 0.996626 (4.67480991e-08)
  3 EPS nconv=1 first unconverged value (error) 0.9353 (3.29361847e-08)
  DOFs = 156384
  keff = 0.99663
  wall = 99.5 sec
average memory = 4.7 Gb
 global memory = 19.0 Gb
$

Utilizando el mismo archivo de entrada pero modificando las opciones de la línea de comando es posible utilizar un solver iterativo para resolver el mismo problema.

$ mpiexec -n 12 feenox iaea-3dpwr-s4.fee --eps_monitor --eps_converged_reason --eps_type=jd --st_type=precond  --st_ksp_type=gmres --st_pc_type=asm
 nodes = 3258
[0/12 tux] solving...
[1/12 tux] solving...
[2/12 tux] solving...
[3/12 tux] solving...
[4/12 tux] solving...
[5/12 tux] solving...
[6/12 tux] solving...
[7/12 tux] solving...
[8/12 tux] solving...
[9/12 tux] solving...
[10/12 tux] solving...
[11/12 tux] solving...
  1 EPS nconv=0 first unconverged value (error) 0.542411 (1.45272351e+02)
  2 EPS nconv=0 first unconverged value (error) 0.988282 (6.81535819e+00)
  3 EPS nconv=0 first unconverged value (error) 0.97111 (4.90651112e+00)
  4 EPS nconv=0 first unconverged value (error) 0.991935 (2.72069261e+00)
  5 EPS nconv=0 first unconverged value (error) 0.995226 (1.46652556e+00)
  6 EPS nconv=0 first unconverged value (error) 0.997734 (6.67104794e-01)
  7 EPS nconv=0 first unconverged value (error) 0.996109 (3.82428107e-01)
  8 EPS nconv=0 first unconverged value (error) 0.996941 (2.46293703e-01)
  9 EPS nconv=0 first unconverged value (error) 0.996638 (1.44292090e-01)
 10 EPS nconv=0 first unconverged value (error) 0.996653 (8.93529784e-02)
 11 EPS nconv=0 first unconverged value (error) 0.99657 (8.93529784e-02)
 12 EPS nconv=0 first unconverged value (error) 0.99657 (7.22756164e-02)
 13 EPS nconv=0 first unconverged value (error) 0.996607 (6.32159213e-02)
 14 EPS nconv=0 first unconverged value (error) 0.996704 (4.36139189e-02)
 15 EPS nconv=0 first unconverged value (error) 0.996642 (2.01286172e-02)
 16 EPS nconv=0 first unconverged value (error) 0.996617 (6.63384323e-03)
 17 EPS nconv=0 first unconverged value (error) 0.996629 (2.39149013e-03)
 Linear eigensolve converged (1 eigenpair) due to CONVERGED_TOL; iterations 18
  DOFs = 156384
  keff = 0.99663
  wall = 613.2 sec
average memory = 1.6 Gb
 global memory = 19.4 Gb

Observación. La malla es ligeramente más gruesa y de menor orden que en los casos resueltos con difusión en la sección anterior. De todas maneras, la cantidad de grados de libertad es comparable al caso quarter de difusión. Pero los recursos computacionales requeridos para resolver un problema de autovalores proveniente de una discretización de ordenadas discretas son significativamente mayores que para difusión.

Observación. Este caso pone en relieve la importancia de la paralelización por MPI: reducir el tiempo de cálculo es un beneficio secundario (que aún debe optimizarse en FeenoX) en comparación con la reducción de la memoria por nodo necesaria para resolver un problema de autovalores con un solver lineal directo. En el caso del solver iterativo, está claro que se intercambia velocidad por memoria.

5.4 El problema de Azmy

TL;DR: Este problema ilustra el “efecto rayo” de la formulación de ordenadas discretas en dos dimensiones. Para estudiar completamente el efecto se necesita rotar la geometría con respecto a las direcciones de S_N.

Figura 5.16: Geometría del problema de Azmy

Este problema adimensional fue introducido en 1988 en el artículo [3] y re-visitado en la tesis de maestría [14]. Consiste en una geometría bi-dimensional muy sencilla, como ilustramos en la figura 5.16. En el paper original, este cuadrado se divide en cuatro cuadrados de 5 \times 5 donde se calculan los flujos medios, que es lo que hacemos en las dos secciones que siguen para comparar los resultados con las referencias.

5.4.1 Malla estructurada uniforme de segundo orden

Aprovechando que la geometría es un cuadrado empezamos resolviendo el problema con una malla estructurada y uniforme de segundo orden (figura 5.17). Mostramos el archivo de entrada de Gmsh para vincular los nombres de las entidades físicas con el archivo de entrada de FeenoX y cómo calculamos los valores medios de los flujos como pide el problema original:

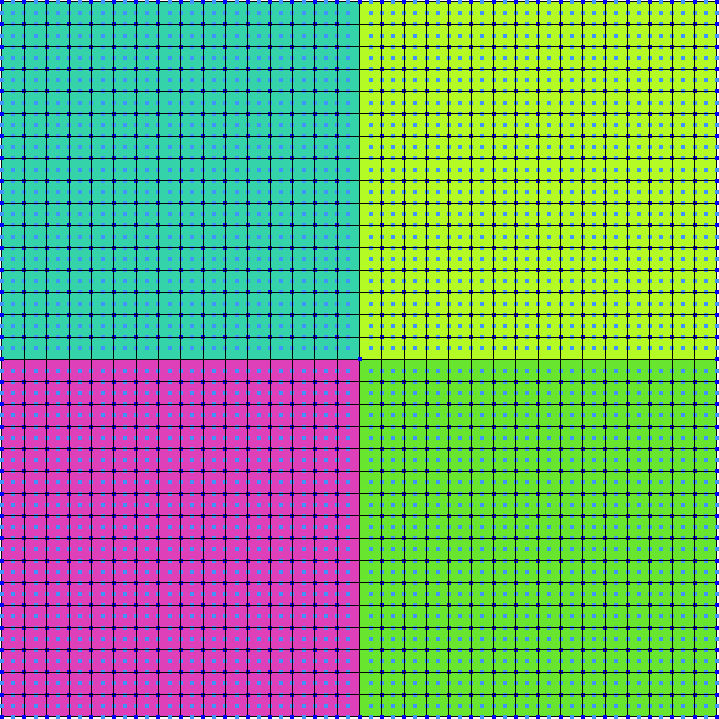
Figura 5.17: Malla cuadrangular estructurada de segundo orden (quad9) para el problema de Azmy

// --- geometría -----------------------------
SetFactory("OpenCASCADE");
a = 5;
b = 10;
Rectangle(1) = {0, 0, 0, a, a};
Rectangle(2) = {a, a, 0, a, a};
Rectangle(3) = {0, a, 0, a, a};
Rectangle(4) = {a, 0, 0, a, a};
Coherence;

// --- grupos físicos ------------------------
// grupos para materiales
Physical Surface("llq",1) = {1}; // lower left
Physical Surface("lrq",2) = {4}; // lower right
Physical Surface("urq",3) = {2}; // upper right
Physical Surface("ulq",4) = {3}; // upper left

// grupos para condiciones de contornos
Physical Curve("mirror", 13) = {10, 4, 1, 11};
Physical Curve("vacuum", 14) = {9, 7, 6, 12};

Transfinite Curve "*" = 1+16;
Transfinite Surface "*";
Mesh.RecombineAll = 1;
Mesh.ElementOrder = 2;
Mesh.SecondOrderIncomplete = 0;

El archivo de entrada de FeenoX es ligeramente más complicado que los anteriores ya que debemos agregar algunas instrucciones para calcular la integral del flujo sobre cada uno de los cuatro cuadrantes con la instrucción INTEGRATE:

DEFAULT_ARGUMENT_VALUE 1 4
PROBLEM neutron_sn DIM 2 GROUPS 1 SN $1

READ_MESH $0.msh

MATERIAL src S1=1 Sigma_t1=1 Sigma_s1.1=0.5
MATERIAL abs S1=0 Sigma_t1=2 Sigma_s1.1=0.1

# vinculación entre grupos físicos 2D y materiales
PHYSICAL_GROUP llq MATERIAL src
PHYSICAL_GROUP lrq MATERIAL abs
PHYSICAL_GROUP urq MATERIAL abs
PHYSICAL_GROUP ulq MATERIAL abs

# vinculación entre grupos físicos 1D y condiciones de contorno
BC mirror   mirror
BC vacuum   vacuum

SOLVE_PROBLEM

# calculamos los valores medios en cada cuadrante
INTEGRATE phi1 OVER llq RESULT lower_left_quadrant
INTEGRATE phi1 OVER lrq RESULT lower_right_quadrant
INTEGRATE phi1 OVER urq RESULT upper_right_quadrant

PRINTF "LLQ = %.3e (ref 1.676e+0)" lower_left_quadrant/(5*5)
PRINTF "LRQ = %.3e (ref 4.159e-2)" lower_right_quadrant/(5*5)
PRINTF "URQ = %.3e (ref 1.992e-3)" upper_right_quadrant/(5*5)

WRITE_RESULTS
PRINTF "%g unknowns for S${1}, memory needed = %.1f Gb" total_dofs memory()

La ejecución de Gmsh y FeenoX da

$ gmsh -2 azmy-structured.geo 
[...]
Info    : 4225 nodes 1225 elements
Info    : Writing 'azmy-structured.msh'...
Info    : Done writing 'azmy-structured.msh'
Info    : Stopped on Sat Oct 21 14:30:23 2023 (From start: Wall 0.0222577s, CPU 0.019616s)
$ feenox azmy-structured.fee 2
LLQ = 1.653e+00 (ref 1.676e+0)
LRQ = 4.427e-02 (ref 4.159e-2)
URQ = 2.712e-03 (ref 1.992e-3)
16900 unknowns for S2, memory needed = 0.1 Gb
$ feenox azmy-structured.fee 4
LLQ = 1.676e+00 (ref 1.676e+0)
LRQ = 4.164e-02 (ref 4.159e-2)
URQ = 1.978e-03 (ref 1.992e-3)
50700 unknowns for S4, memory needed = 0.8 Gb
$ feenox azmy-structured.fee 6
LLQ = 1.680e+00 (ref 1.676e+0)
LRQ = 4.120e-02 (ref 4.159e-2)
URQ = 1.874e-03 (ref 1.992e-3)
101400 unknowns for S6, memory needed = 3.3 Gb
$

5.4.2 Malla no estructurada localmente refinada de primer orden

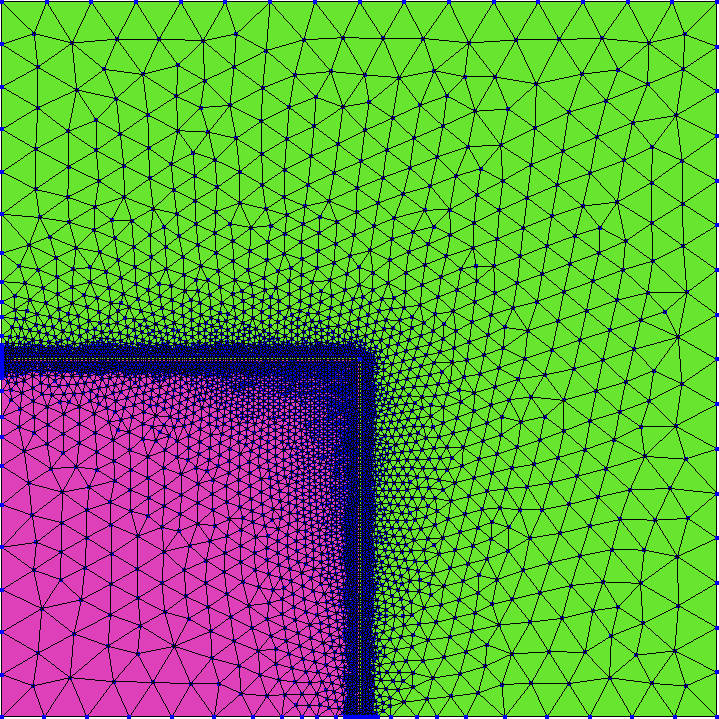
Dado que es esperable que haya grandes gradientes en el flujo neutrónico en las interfaces entre la zona de la fuente y el reflector, podemos aprovechar la posibilidad de hacer un refinamiento local en mallas no estructuradas (figura 5.18). Para ilustrar la flexibilidad de FeenoX, ahora no asignamos una entidad física a cada cuadrante sino que integramos el flujo con el funcional integrate dando explícitamente el dominio de integración como función de x e y.

// --- geometry -------------------------------------------------
SetFactory("OpenCASCADE");
a = 5;
b = 10;
Rectangle(1) = {0, 0, 0, a, a};
Rectangle(2) = {0, 0, 0, b, b};
Coherence;

// --- physical groups ------------------------------------------
Physical Surface("src") = {1};
Physical Surface("abs") = {2};
Physical Curve("mirror") = {3, 8, 7, 6};
Physical Curve("vacuum") = {4, 5};

// --- meshing options ------------------------------------------
n1 = 8;
n2 = 96;
Mesh.MeshSizeMax = a/n1;
Mesh.MeshSizeMin = a/n2;

Mesh.Algorithm = 6;
Mesh.Optimize = 1;
Mesh.OptimizeNetgen = 1;
Mesh.RecombineAll = 0;
Mesh.ElementOrder = 1;

// local refinements
Field[1] = Distance;
Field[1].CurvesList = {1,2};
Field[1].Sampling = 100;
Field[2] = Threshold;
Field[2].IField = 1;
Field[2].LcMin = Mesh.MeshSizeMin;
Field[2].LcMax = Mesh.MeshSizeMax;
Field[2].DistMin = 4*Mesh.MeshSizeMin;
Field[2].DistMax = 8*Mesh.MeshSizeMin;
Background Field = {2};

DEFAULT_ARGUMENT_VALUE 1 4
PROBLEM neutron_sn DIM 2 GROUPS 1 SN $1

READ_MESH $0.msh

# podemos dar las secciones eficaces a través de variables
S1_src = 1
Sigma_t1_src = 1
Sigma_s1.1_src = 0.5

S1_abs = 0
Sigma_t1_abs = 2
Sigma_s1.1_abs = 0.1

BC mirror   mirror
BC vacuum   vacuum

SOLVE_PROBLEM

# calculamos los valores medios con integrales dobles sobre x e y
lower_left_quadrant = integral(integral(phi1(x,y),y,0,5),x,0,5)/(5*5)
lower_right_quadrant = integral(integral(phi1(x,y),y,0,5),x,5,10)/(5*5)
upper_right_quadrant = integral(integral(phi1(x,y),y,5,10),x,5,10)/(5*5)

PRINT %.3e "LLQ" lower_left_quadrant  "(ref 1.676e+0)"
PRINT %.3e "LRQ" lower_right_quadrant "(ref 4.159e-2)"
PRINT %.3e "URQ" upper_right_quadrant "(ref 1.992e-3)"

WRITE_RESULTS
PRINTF "%g unknowns for S${1}, memory needed = %.1f Gb" total_dofs memory()

$ gmsh -2 azmy.geo 
[...]
Info    : 3926 nodes 8049 elements
Info    : Writing 'azmy.msh'...
Info    : Done writing 'azmy.msh'
Info    : Stopped on Sat Oct 21 14:44:46 2023 (From start: Wall 0.129908s, CPU 0.127121s)
$ feenox azmy.fee 2
LLQ     1.653e+00       (ref 1.676e+0)
LRQ     4.427e-02       (ref 4.159e-2)
URQ     2.717e-03       (ref 1.992e-3)
15704 unknowns for S2, memory needed = 0.1 Gb
$ feenox azmy.fee 4
LLQ     1.676e+00       (ref 1.676e+0)
LRQ     4.160e-02       (ref 4.159e-2)
URQ     1.991e-03       (ref 1.992e-3)
47112 unknowns for S4, memory needed = 0.5 Gb
$ feenox azmy.fee 6
LLQ     1.680e+00       (ref 1.676e+0)
LRQ     4.115e-02       (ref 4.159e-2)
URQ     1.890e-03       (ref 1.992e-3)
94224 unknowns for S6, memory needed = 1.9 Gb
$

Figura 5.18: Malla triangular no estructurada de primer orden (tri3) para el problema de Azmy

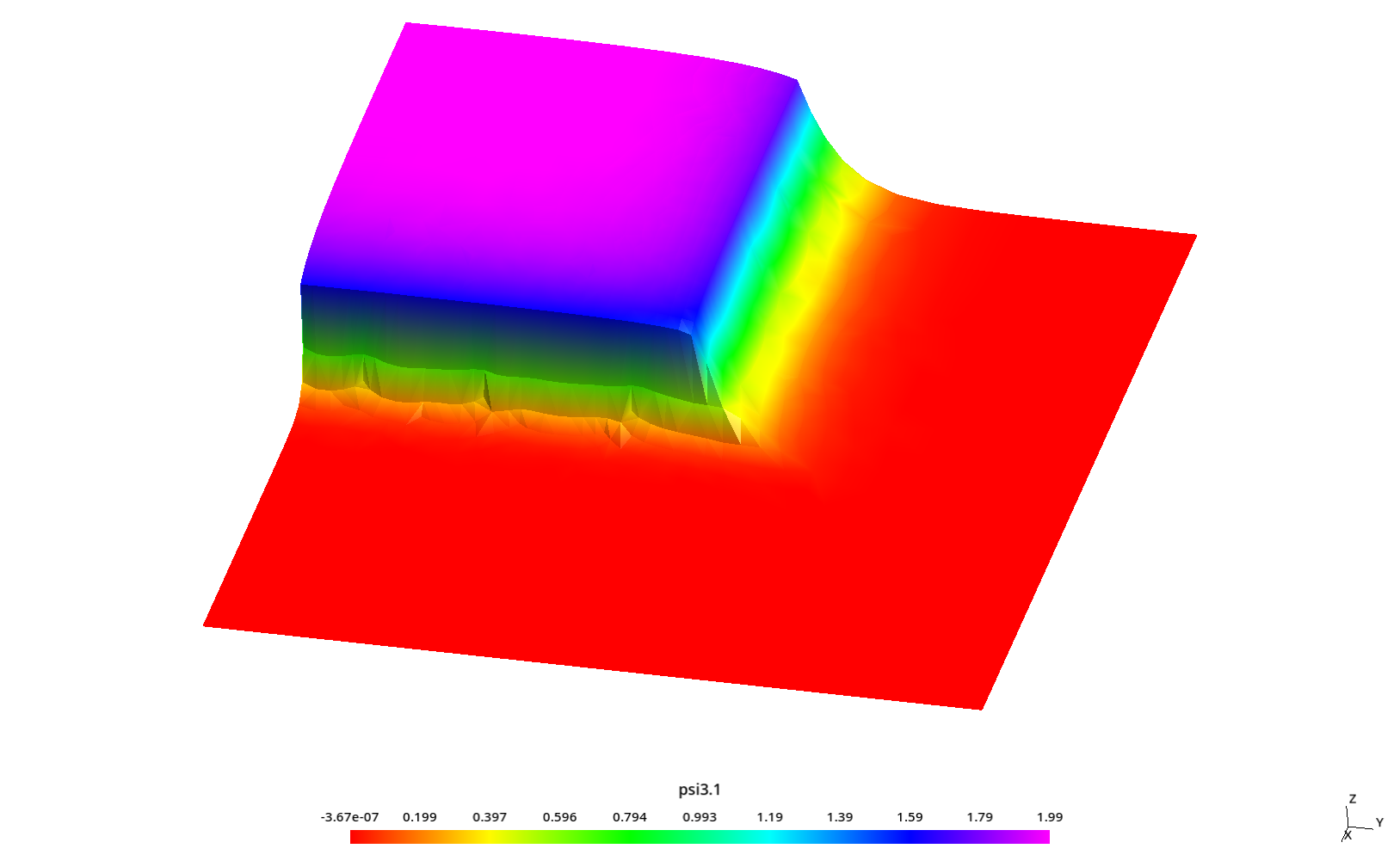
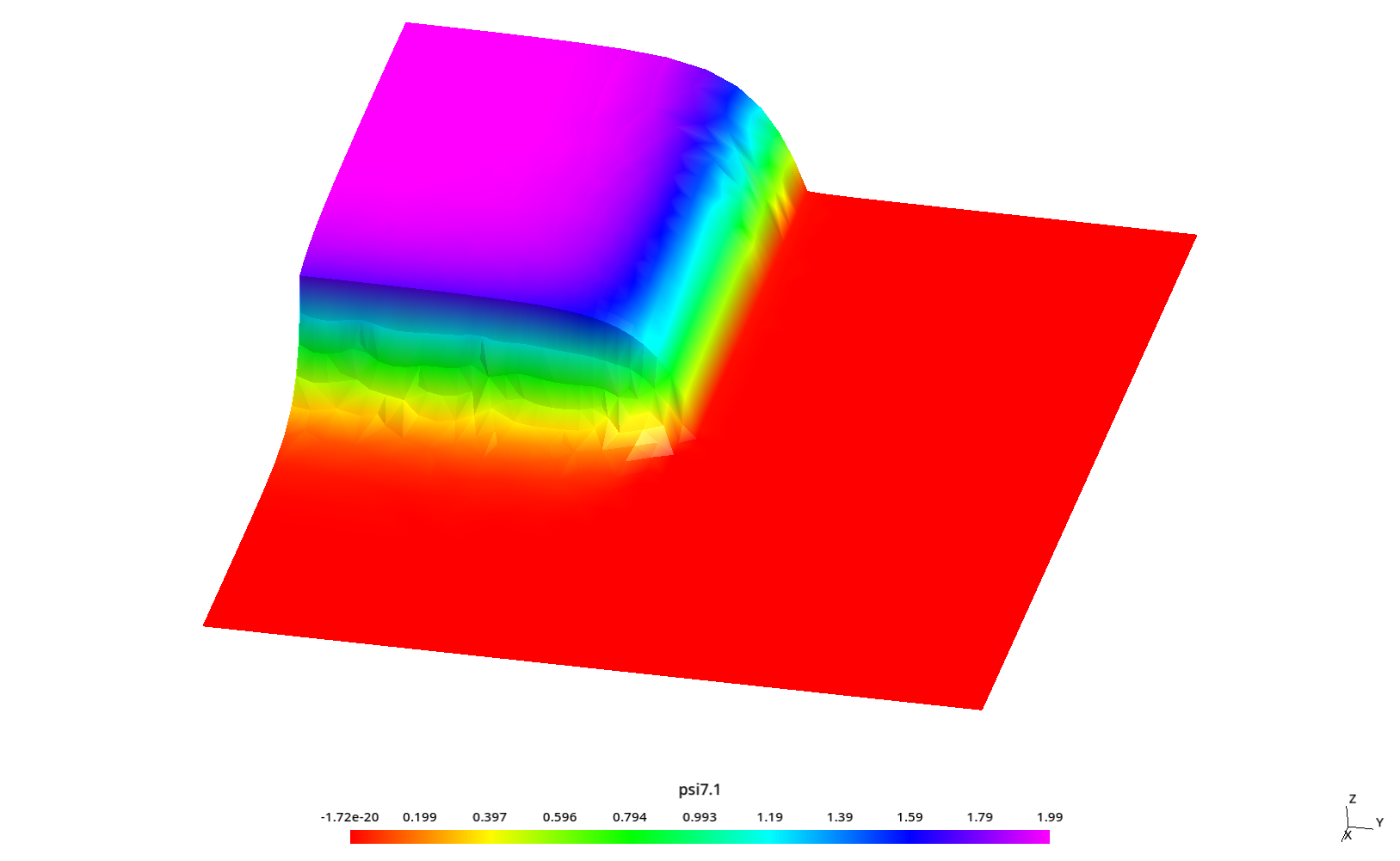
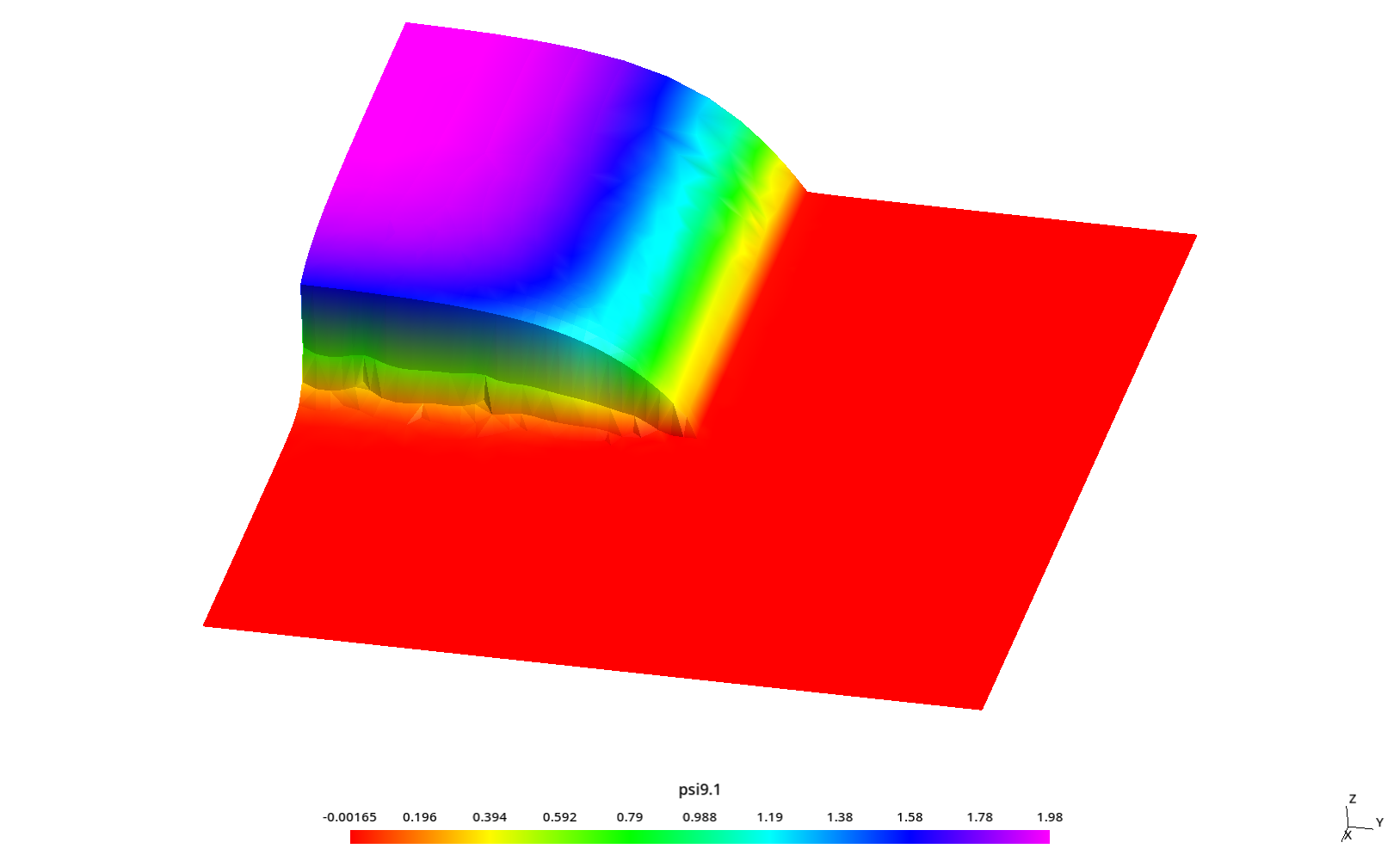
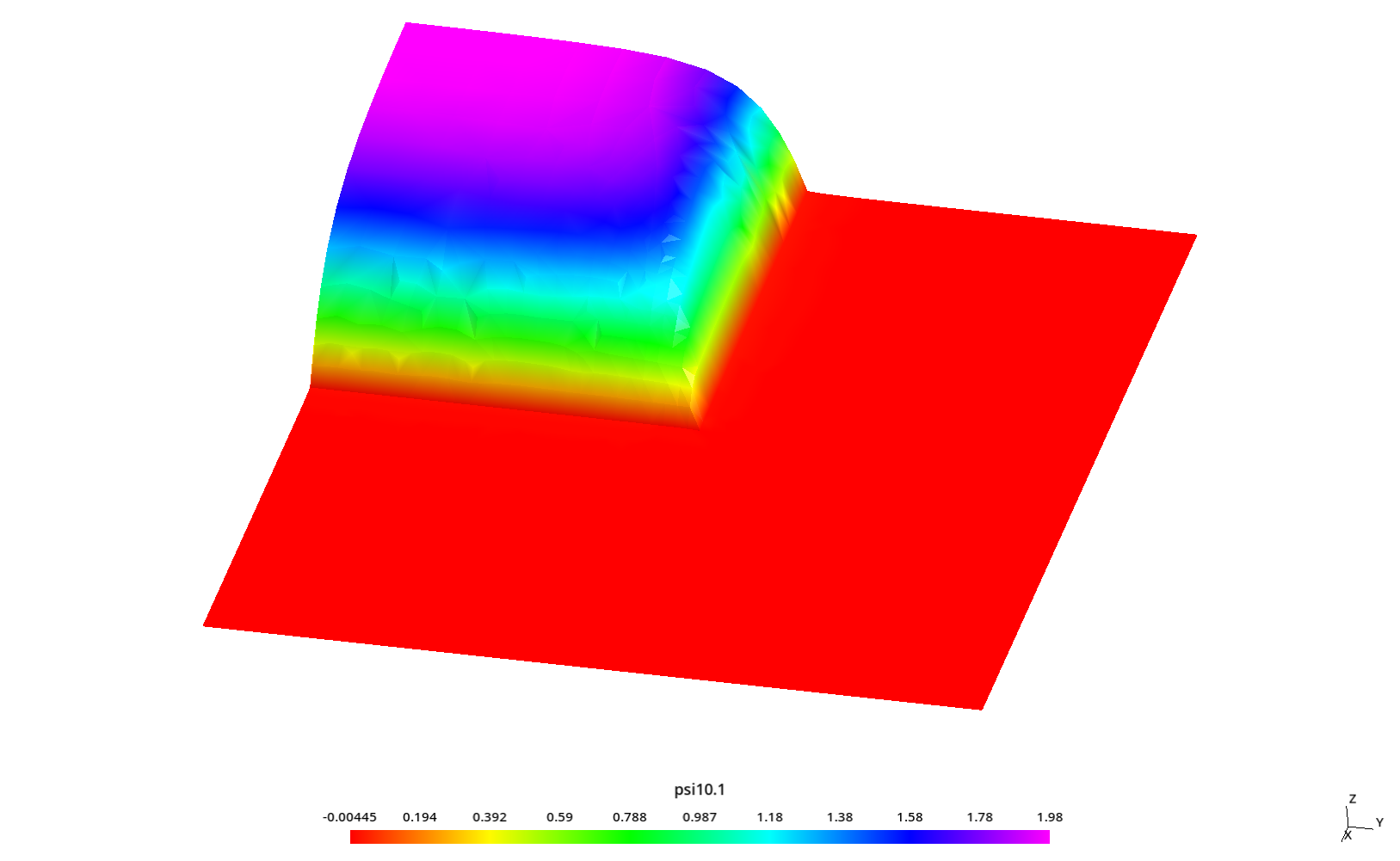
5.4.3 Estudio paramétrico para analizar el “efecto rayo”

En la ref. [14], el autor nota que este tipo de problemas es susceptible al artefacto numérico conocido como “efecto rayo” según el cual la discretización angular hace que algunas direcciones no estén bien representadas por el esquema de S_N. Justamente en esa tesis se proponen formas para lidiar con este efecto. Incluso una de esas formas es discretizar la variable angular con funciones de forma similares a las usadas para discretizar el espacio [11].

Para ilustrar el efecto, se toman perfiles de flujo a lo largo de la dirección y para diferentes valores constantes de x sobre el reflector (donde el flujo es mucho menor que en la fuente como ilustramos en las figuras 5.19 y 5.20. En particular, el autor investiga los siguientes tres valores de x

x=5.84375
x=7.84375
x=9.84375

Para poder entender lo que está pasando, queremos estudiar qué sucede con estos perfiles cuando las direcciones de S_N de alguna manera “rotan” con respecto a la geometría. Como FeenoX usa cuadraturas de nivel simétrico, no podemos rotar las direcciones. Debemos rotar la geometría. Pero si rotamos un ángulo arbitrario \theta el cuadrado original no vamos a poder poner las condiciones de simetría ya que se necesita que tanto la dirección incidente como la reflejada estén en el conjunto de cuadraturas. Por lo tanto necesitamos modelar la geometría completa de tamaño 20 \times 20 con condiciones de contorno de vacío en los cuatro lados del cuadrado.

Además del ángulo \theta \leq 45° de rotación de la geometría alrededor del eje z saliendo de la pantalla (o papel si usted está leyendo esta tesis analógicamente), también queremos estudiar qué pasa si variamos la densidad de mallado espacial y angular. Por eso recurrimos a un estudio paramétrico sobre

el ángulo \theta
un factor c de escala de malla
N=4,6,8,10,12

Observación. Este caso ilustra la explosión combinatoria de resultados a analizar al realizar estudios paramétricos.

Para eso preparamos un archivo de entrada de Gmsh que

toma un argumento theta y lo asigna a una variable angle para rotar la geometría,
define el tamaño de la malla según el factor de escala pasado en la línea de comandos -clscale

SetFactory("OpenCASCADE");
a = 5;
b = 10;
Rectangle(1) = {-a, -a, 0, 2*a, 2*a};
Rectangle(2) = {a, a, 0, a, a};
Rectangle(3) = {-a, a, 0, 2*a, a};
Rectangle(4) = {a, -a, 0, a, 2*a};
Rectangle(5) = {-2*a, a, 0, a, a};
Rectangle(6) = {-2*a, -a, 0, a, 2*a};
Rectangle(7) = {-2*a, -2*a, 0, a, a};
Rectangle(8) = {-a, -2*a, 0, 2*a, a};
Rectangle(9) = {a, -2*a, 0, a, a};
Coherence;

Rotate {{0, 0, 1}, {0, 0, 0}, angle*Pi/180} {
  Surface{5}; Surface{6}; Surface{7}; Surface{3}; Surface{1}; Surface{8}; Surface{4}; Surface{2}; Surface{9}; 
}

Physical Surface("src", 1) = {1};
Physical Surface("abs", 2) = {4, 2, 3, 5, 6, 7, 8, 9};
Physical Curve("vacuum", 49) = {28, 31, 34, 32, 40, 47, 48, 43, 45, 46, 37, 27};

n = 40/Mesh.MeshSizeFactor;
Transfinite Curve {31, 30, 39, 43, 37, 35, 38, 40} = 1+2*n;
Transfinite Curve {28, 26, 36, 45, 34, 33, 41, 48, 27, 25, 29, 32, 46, 44, 42, 47} = 1+n;
Transfinite Surface "*";
Mesh.RecombineAll = 1;
Mesh.ElementOrder = 1;
Mesh.SecondOrderIncomplete = 0;

Por otro lado, el archivo de entrada de FeenoX toma los tres parámetros a estudiar en la línea de comando. Una vez resuelto el problema neutrónico, define tres funciones de una única variable igual a los perfiles de flujo pedidos en la geometría original con \theta = 0 y los escribe en un archivo de texto ASCII listos para ser graficados con herramientas como Gnuplot o Pyxplot:

DEFAULT_ARGUMENT_VALUE 1 0   # theta
DEFAULT_ARGUMENT_VALUE 2 4   # N
DEFAULT_ARGUMENT_VALUE 3 0   # c
PROBLEM neutron_sn DIM 2 GROUPS 1 SN $2

READ_MESH $0-$1.msh

MATERIAL src S1=1 Sigma_t1=1 Sigma_s1.1=0.5
MATERIAL abs S1=0 Sigma_t1=2 Sigma_s1.1=0.1
BC vacuum   vacuum

SOLVE_PROBLEM

# un poco de trigonometría de prescolar
theta = $1*pi/180
x'(d,x) = d*cos(theta) - x*sin(theta)
y'(d,x) = d*sin(theta) + x*cos(theta)

# perfiles a lo largo de líneas c=cte (en la geometría original)
profile5(x) = phi1(x'(5.84375,x), y'(5.84375,x))
profile7(x) = phi1(x'(7.84375,x), y'(7.84375,x))
profile9(x) = phi1(x'(8.84375,x), y'(9.84375,x))

PRINT_FUNCTION profile5 profile7 profile9 MIN -10 MAX 10 NSTEPS 1000 FILE $0-$1-$2-$3.dat

PRINTF "%g unknowns for S${2} scale factor = ${3}, memory needed = %.1f Gb" total_dofs memory()

Finalmente necesitamos un script driver que llame sucesivamente a Gmsh y a FeenoX con las combinaciones de parámetros apropiados. Podemos usar Bash para esto:

#!/bin/bash

thetas="0 15 30 45"
cs="4 3 2 1.5 1"
sns="4 6 8 10 12"

for theta in ${thetas}; do
 echo "angle = ${theta};" > azmy-angle-${theta}.geo
 for c in ${cs}; do
  gmsh -v 0 -2 azmy-angle-${theta}.geo azmy-full.geo -clscale ${c} -o azmy-full-${theta}.msh
  for sn in ${sns}; do
   if [ ! -e azmy-full-${theta}-${sn}-${c}.dat ]; then
     echo ${theta} ${c} ${sn}
     feenox azmy-full.fee ${theta} ${sn} ${c} --progress
   fi
  done
 done
done

De los muchos archivos con resultados y de las muchas maneras de combinar los perfiles obtenidos, mostramos algunas de las figuras resultantes a continuación. Comencemos con \theta=0 (es decir la geometría original) para N=4, N=8 y N=12 para ver como el perfil “mejora” (figuras 5.21–5.23). Ahora fijemos c y veamos qué pasa para diferentes ángulos. Algunos valores de \theta son “peores” que otros. Parecería que \theta=45º da la “mejor” solución (figuras 5.24–5.27). Para un factor de refinamiento espacial fijo c=1 está claro que aumentar N mejora los perfiles (figuras 5.28–5.30). Finalmente podemos ver cómo cambian los perfiles con el ángulo \theta para las mallas más finas (figuras 5.31–5.32).

Figura 5.21: \theta=0 y N=4 para diferentes valores de c

Figura 5.22: \theta=0 y N=8 para diferentes valores de c

Figura 5.23: \theta=0 y N=12 para diferentes valores de c

Figura 5.24: \theta=0 y c=1.5 para diferentes valores de $N

Figura 5.25: \theta=15 y c=1.5 para diferentes valores de N

Figura 5.26: \theta=30 y c=1.5 para diferentes valores de N

Figura 5.27: \theta=45 y c=1.5 para diferentes valores de N

Figura 5.28: N=4 y c=1 para diferentes valores de \theta

Figura 5.29: N=6 y c=1 para diferentes valores de \theta

Figura 5.30: N=9 y c=1 para diferentes valores de \theta

Figura 5.31: N=10 y c=1.5 para diferentes valores de \theta

Figura 5.32: N=12 y c=2 para diferentes valores de \theta

Observación. El análisis detallado del efecto rayo en ordenadas discretas es un posible trabajo futuro derivado de esta tesis de doctorado.

5.5 Benchmarks de criticidad de Los Alamos

TL;DR: Estos problemas proveen una manera de realizar una primera verificación del código con el método de soluciones exactas.

El proceso de verificación de un código numérico involucra justamente, verificar que las ecuaciones se estén resolviendo bien.⁷ La forma estricta de realizarlo es comparar alguna medida del error cometido en la solución numérica con respecto a la solución exacta de la ecuación que estamos resolviendo y mostrar que éste tiende a cero con el orden teórico según el método numérico empleado [13]. En particular, la incógnita primaria de una ecuación en derivadas parciales discretizada con el método de elementos finitos debe ir a cero con un order superior en una unidad al orden de los elementos utilizados. Las incógnitas secundarias, con el mismo orden. Es decir, los desplazamientos en elasticidad y las temperaturas en conducción de calor deben converger a cero como h^3 y las tensiones y los flujos de calor como h^2 si h es el tamaño característico de los elementos de segundo orden utilizados para discretizar el dominio del problema.

Una de las dificultades de la verificación consiste en encontrar la solución de referencia con la cual calcular la medida del error numérico cometido. En la Sección 5.9 proponemos una alternativa utilizando el método de soluciones fabricadas,⁸ pero en esta sección tomamos algunos de los 75 casos resueltos en la referencia [23] que incluyen

problemas a uno, dos, tres y seis grupos de energía
scattering isotrópico y linealmente anisótropo
geometrías
- de medio infinito
- de slab en 1D
- de círculo en 2D
- de esfera en 2D
dominios de uno o varios materiales

El informe provee

el factor de multiplicación efectivo infinito k_\infty, o
el tamaño crítico

de cada una de las 75 configuraciones de reactores en geometrías triviales para diferentes conjuntos de secciones eficaces macroscópicas uniformes a zonas. Cada una de ellas se identifica con una cadena que tiene la forma

Por ejemplo UD2O-H2O(10)-1-0-SL indica un reactor de uranio y D_2O con un reflector de H_2O de 10 caminos libres medios de espesor, un grupo de energías, scattering isotrópico en geometría tipo slab.

5.5.1 Casos de medio infinito

Una forma de implementar un medio infinito en FeenoX es utilizar una geometría unidimensional tipo slab y poner condiciones de contorno de simetría en ambos extremos. Como el k_\infty no depende ni de la cantidad de nodos espaciales ni de la cantidad de direcciones angulares, reportamos directamente la diferencia entre el k_\text{eff} calculado por FeenoX con S_2 y el k_\infty de la referencia:

Tabla 5.5: Factores de multiplicación de medio infinito con las cifras significativas reportadas en [23] y diferencia con respecto al k_\text{eff} calculado con FeenoX con S_2.
Problema	Identificador	k_\infty	k_\infty - k_\text{eff}
01	PUa-1-0-IN	2.612903	+2.3 \times 10^{-7}
05	PUb-1-0-IN	2.290323	+3.6 \times 10^{-7}
47	U-2-0-IN	2.216349	-4.6 \times 10^{-7}
50	UAl-2-0-IN	2.661745	-4.2 \times 10^{-7}
70	URRa-2-1-IN	1.631452	-2.5 \times 10^{-6}
74	URR-3-0-IN	1.60	+2.7 \times 10^{-15}
75	URR6-6-0-IN	1.60	+5.2 \times 10^{-14}

Observación. Está claro que la diferencia k_\infty - k_\text{eff} es menor a la precisión del k_\infty dado en la referencia y que los problemas 74 y 75 han sido “manufacturados” para que el factor infinito sea exactamente igual a 8/5.

Para ilustrar cómo hemos obtenido la tabla 5.5 mostramos a continuación el archivo de entrada del caso 74:

# Los Alamos LA-13511 Analytical Benchmark Test Set for Criticallity Code Verification
# problem 74
PROBLEM neutron_sn 1D GROUPS 3 SN 2
READ_MESH la-IN.msh
INCLUDE URR.fee
BC mirror  mirror
penalty_weight = 10
SOLVE_PROBLEM
PRINT %+.1e keff-1.60

Figura 5.33: Secciones eficaces macroscópicas a tres grupos del material URR [23].

Como las secciones eficaces son las mismas para varios problemas, cada material tiene un archivo separado que se incluye desde cada entrada principal. En este caso, a partir de los datos originales mostrados en la figura 5.33, preparamos el archivo URR.fee:

# material Research Reactor (tables 59, 60 and 61)
# NOTE: 1 is the slow energy grop and 3 is the fast energy group
# fast-energy group
nu3_fuel = 3.0
Sigma_f3_fuel = 0.006
nuSigma_f3_fuel = nu3_fuel*Sigma_f3_fuel

Sigma_s3.3_fuel     = 0.024
Sigma_s3.2_fuel     = 0.171
Sigma_s3.1_fuel     = 0.033

Sigma_t3_fuel   = 0.240
chi[3] = 0.96

# middle-energy group
nu2_fuel = 2.5
Sigma_f2_fuel = 0.060
nuSigma_f2_fuel = nu2_fuel*Sigma_f2_fuel

Sigma_s2.3_fuel     = 0
Sigma_s2.2_fuel     = 0.60
Sigma_s2.1_fuel     = 0.275

Sigma_t2_fuel   = 0.975
chi[2] = 0.04

# slow energy group
nu1_fuel = 2.0
Sigma_f1_fuel = 0.90
nuSigma_f1_fuel = nu1_fuel*Sigma_f1_fuel

Sigma_s1.3_fuel     = 0
Sigma_s1.2_fuel     = 0
Sigma_s1.1_fuel     = 2.0

Sigma_t1_fuel   = 3.10
chi[1] = 0.0

Observación. La definición de los grupos en la referencia [23] es opuesta a la de la mayoría de la literatura: el grupo uno es el térmico y el de mayor energía es el de mayor índice g.

5.5.2 Casos de medio finito

La forma de “verificar” que FeenoX resuelve razonablemente bien problemas de transporte de neutrones con dependencia espacial es entonces

crear una malla con el tamaño indicado como crítico en cada problema, y
mostrar que el factor de multiplicación efectivo k_\text{eff} obtenido se acerca a la unidad a medida que aumentamos el tamaño del problema discretizado, sea por refinar la malla espacial o por aumentar el número N de ordenadas discretas.

Para ello podemos crear un script de Bash que llame a cada uno de los archivos de entrada de cada problema, luego de haber creado mallas con diferente refinamiento, con valores de N sucesivos:

#!/bin/bash

for p in $(ls la-*.fee | grep -v IN); do
 rm -f tmp
 for c in 1 0.75 0.65 0.60 0.55 0.5; do
  gmsh -v 0 -3 $(basename ${p} .fee).geo -clscale ${c}   
  for N in 2 4 6 8; do
   feenox ${p} $N | tee -a tmp
  done
 done
 sort -g tmp > $(basename ${p} .fee).csv
done

Figura 5.34: Factor de multiplicación vs. cantidad de grados de libertad para 13 de los 75 problemas de [23]. A medida que aumentamos el tamaño del problema (sea por refinamiento de malla o por incrementar N) el k_\text{eff} se acerca a la unidad.

La figura 5.34 muestra—en forma poco rigurosa—que en general al aumentar el tamaño del problema resuelto por FeenoX, el factor de multiplicación efectivo se acerca a la unidad. Esta no es una verificación según la definición industrial de “code verification” pero indica que nuestro solver hace las cosas razonablemente bien, incluso en casos con scattering anisótropo y con más de dos grupos de energías.

5.6 Slab a dos zonas: efecto cúspide por dilución de XSs

TL;DR: Este problema ilustra el error cometido al analizar casos multi-material con mallas estructuradas donde la interfaz no coincide con los nodos de la malla (y la flexibilidad de FeenoX para calcular y comparar soluciones analíticas con soluciones numéricas).

Richard Stallman dice en sus conferencias (incluso en castellano) “la mejor manera de resolver un problema es evitar tenerlo”. Como discutimos en la Sección 1.2, los códigos neutrónicos de núcleo que usamos durante el completamiento de la Central Nuclear Atucha II solamente usaban mallas estructuradas. Además del inconveniente que esto supone para modelar barras de control invertidas, muy a menudo teníamos que lidiar con un efecto numérico denominado “cúspide por dilución de secciones eficaces”. Este efecto aparece cuando la posición de una barra de control no coincide con la interfaz entre dos celdas de cálculo y hay que de alguna manera “diluir” las secciones eficaces de la barra absorbente entre las secciones eficaces del tubo guía vacío en forma proporcional a la posición geométrica de la barra en la celda de cálculo.

Es exactamente este efecto el que ilustramos en este ejemplo, pero en geometría tipo slab ya que dicho problema tiene solución analítica exacta (en difusión, que es lo que usaban los códigos en Atucha de cualquier manera). Efectivamente, consideremos un reactor en geometría slab a dos zonas, como ilustramos en la figura 5.35:

La zona A tiene k_\infty < 1 y ocupa el intervalo 0<x=a, y
La zona B tiene k_\infty > 1 y ocupa el intervalo a<x<b.

Figura 5.35: Slab a dos zonas, una A con k_\infty < 1 y otra B con k_\infty > 1

resolvemos el slab con un grupo de energías con aproximación de difusión,
las dos zonas tienen secciones eficaces macroscópicas uniformes, y
hacemos que el flujo escalar \phi sea cero en ambos extremos x=0 y x=b,

entonces el factor efectivo de multiplicación k_\text{eff} es tal que

\begin{aligned} \sqrt{D_A\cdot\left(\Sigma_{aA}- \frac{\nu\Sigma_{fA}}{k_\text{eff}}\right)} \cdot \tan\left[\sqrt{\frac{1}{D_B} \cdot\left( \frac{\nu\Sigma_{fB}}{k_\text{eff}}-\Sigma_{aB} \right) }\cdot (a-b) \right] \\ - \sqrt{D_B\cdot\left(\frac{\nu\Sigma_{fB}}{k_\text{eff}}-\Sigma_{aB}\right)} \cdot \tanh\left[\sqrt{\frac{1}{D_A} \cdot\left( \Sigma_{aA}-\frac{\nu\Sigma_{fA}}{k_\text{eff}} \right)} \cdot b\right] = 0 \end{aligned} \tag{5.1}

Observación. Aunque no lo parezca, esta ecuación 5.1 es la solución analítica para k_\text{eff}. Lo que hay que hacer para obtener su valor es resolver esta ecuación implícita, cosa que FeenoX puede hacer perfectamente como mostramos a continuación.

Observación. Este problema no sólo tiene solución analítica para el factor k_\text{eff} sino que también el flujo \phi(x) tiene una expresión algebraica por trozos para 0 < x < a y para a < x < b. De hecho una para x<a y otra para x>a. Dicha solución no es relevante para este problema, pero por completitud dejamos comentadas las instrucciones de FeenoX para evaluarlo y escribirlo en un archivo de salida.

Por otro lado, vamos a calcular k_\text{eff} numéricamente de dos maneras diferentes, a saber:

usando una malla no uniforme con n elementos y n+1 nodos de forma tal que siempre haya un nodo exactamente en la interfaz x=a para cualquier valor arbitrario de b, y
con una malla uniforme con n elementos de igual tamaño y n+1 nodos equi-espaciados para emular el comportamiento de los solvers que no pueden manejar el caso i. Si la interfaz coincide exactamente con uno de los nodos, entonces hay dos zonas bien definidas (figura 5.36 (a)). Pero en general, esto no va a suceder (figura 5.36 (b)). Entonces, al elemento que contiene la interfaz x=a le asignamos un pseudo material AB (figura 5.36 (c)) cuyas secciones eficaces son un promedio pesado de las de A y B según la fracción geométrica que cada una de las zonas ocupa en el elemento. Es decir, si b=100 y n=10 entonces cada elemento tiene un ancho igual a 10. Si además a=52 entonces este material AB tendrá un 20% del material A y un 80% del material B.

Para ello, preparamos dos archivos de Gmsh. Primero two-zone-slab-i.geo para el caso no uniforme (que es más sencillo para Gmsh que el caso uniforme):

Merge "ab.geo";

Point(1) = {0, 0, 0, lc+lc/n};
Point(2) = {a, 0, 0, lc+lc/n};
Point(3) = {b, 0, 0, lc+lc/n};

Line(1) = {1, 2};
Line(2) = {2, 3};
Physical Line("A", 1) = {1};
Physical Line("B", 2) = {2};

Physical Point("left") = {1};
Physical Point("right") = {3};

y luego el archivo two-zone-slab-ii.geo:

Merge "ab.geo";
a_left  = Floor(a/lc)*lc;
a_right = (Floor(a/lc)+1)*lc;

Point(1) = {0, 0, 0, lc};
Point(2) = {a_left, 0, 0, lc};
Point(3) = {a_right, 0, 0, lc};
Point(4) = {b, 0, 0, lc};

Line(1) = {1, 2};
Line(2) = {2, 3};
Line(3) = {3, 4};
Physical Line("A", 1) = {1};
Physical Line("AB", 3) = {2};
Physical Line("B", 2) = {3};

Physical Point("left") = {1};
Physical Point("right") = {4};

Ambos necesitan un archivo ab.geo con la definición de las variables geométricas necesarias:

// dimensiones del slab
a = 57;
b = 100;
// número de elementos
n = 20;
// longitud característica
lc = b/n;

La figura 5.37 muestra la diferencia entre los dos casos i (no uniforme) y ii (uniforme) para n=10. Cuando a=55 (figura 5.37 (a)), en la malla i hay cinco elementos en cada una de las dos zonas. Los elementos de la zona A son ligeramente más grandes que los de la zona B. En la malla ii todos los elementos son iguales. Hay cinco elementos en la zona A, uno en la zona AB y cuatro en la zona B. Para a=72 (figura 5.37 (b)), hay siete elementos a la izquierda de x=a y tres a la derecha en el caso i. En el caso ii, hay siete elementos en la zona A, uno en la zona AB y dos en la zona B.

Ahora preparamos este archivo de entrada de FeenoX que es de los más complicados (pero a la vez de los más flexibles) que hemos visto hasta el momento:

PROBLEM neutron_diffusion 1D
DEFAULT_ARGUMENT_VALUE 1 i

# leemos la malla según el argumento sea i o ii
READ_MESH two-zone-slab-$1.msh

# este archivo ab.geo tiene información geométrica y es creado
# por el script en bash que nos llama
INCLUDE ab.geo

# XSs para el material puro A de x=0 to x=a
D1_A = 0.5
Sigma_a1_A = 0.014
nuSigma_f1_A = 0.010

# XSs para el material puro B de x=a to x=b
D1_B = 1.2
Sigma_a1_B = 0.010
nuSigma_f1_B = 0.014

# psedo-material AB usado solamente si $1 es uniform
a_left  = floor(a/lc)*lc;
xi = (a - a_left)/lc
Sigma_tr_A = 1/(3*D1_A)
Sigma_tr_B = 1/(3*D1_B)
Sigma_tr_AB = xi*Sigma_tr_A + (1-xi)*Sigma_tr_B
D1_AB = 1/(3*Sigma_tr_AB)
Sigma_a1_AB = xi * Sigma_a1_A + (1-xi)*Sigma_a1_B
nuSigma_f1_AB = xi * nuSigma_f1_A + (1-xi)*nuSigma_f1_B

# condiciones de contorno de flujo nulo
BC left  phi1=0
BC right phi1=0

SOLVE_PROBLEM

# calculamos el keff analítico como la raíz de F1(k)-F2(k)
F1(k) = sqrt(D1_A*(Sigma_a1_A-nuSigma_f1_A/k)) * tan(sqrt((1/D1_B)*(nuSigma_f1_B/k-Sigma_a1_B))*(a-b))
F2(k) = sqrt(D1_B*(nuSigma_f1_B/k-Sigma_a1_B)) * tanh(sqrt((1/D1_A)*(Sigma_a1_A-nuSigma_f1_A/k))*b)
k = root(F1(k)-F2(k), k, 1, 1.2)

# el flujo analítico en función de x (no es usado en este problema)
B_A = sqrt((Sigma_a1_A - nuSigma_f1_A/k)/D1_A)
fluxA(x) = sinh(B_A*x)

B_B = sqrt((nuSigma_f1_B/k - Sigma_a1_B)/D1_B)
fluxB(x)= sinh(B_A*b)/sin(B_B*(a-b)) * sin(B_B*(a-x))

# factor de normalización
f = a/(integral(fluxA(x), x, 0, b) + integral(fluxB(x), x, b, a))
flux(x) := f * if(x < b, fluxA(x), fluxB(x))

# esribimos keff (numerico) y k (analitico) vs. a
PRINT a keff k keff-k

# si quisiéramos, con estas líneas podríamos comparar los flujos
# PRINT_FUNCTION flux MIN 0 MAX a STEP a/1000 FILE_PATH two-zone-analytical.dat
# PRINT_FUNCTION phi1 phi1(x)-flux(x)         FILE_PATH two-zone-numerical.dat

La ejecución necesita un argumento que puede ser i o ii según sea el punto que queremos resolver:

malla no uniforme
malla uniforme

Cada uno de los dos puntos usa una malla diferente, que luego explicamos cómo generamos. Luego incluimos el mismo archivo ab.geo con la información geométrica que ya incluyeron los archivos de entradas de Gmsh. Como la sintaxis de asignación de variables es igual en Gmsh que en Feenox, podemos incluirlo directamente (el punto y coma al finalizar la línea es opcional en FeenoX).

A continuación definimos las secciones eficaces de los dos materiales asignando variables y finalmente calculamos las secciones eficaces del pseudo-material AB utilizando las facilidades algebraicas que nos provee FeenoX. Ponemos condiciones de contorno nulas, resolvemos el problema y tenemos en la variable especial keff el factor de multiplicación efectiva para una posición a de la interfaz en un slab de ancho b en el caso i (no uniforme) o ii (uniforme).

Lo que queremos ahora es comparar este keff numérico con el k_\text{eff} analítico para cuantificar los errores producidos por los métodos i y ii. Procedemos entonces a resolver (numéricamente) la ecuación 5.1 con el funcional root() y almacenamos el resultado en la variable k, que luego podemos imprimir en la salida estándar y redireccionar a un archivo de texto para graficar estas diferencias.

Observación. Hemos necesitado resolver numéricamente la ecuación 5.1 para obtener el k_\text{eff}, pero éste sigue siendo un valor analítico. La búsqueda numérica de la raíz de la ecuación es un algoritmo que puede continuar hasta que el error cometido sea arbitrariamente pequeño, por lo que k es analítico y keff numérico.

Nos falta un archivo más para completar el estudio, que es un script que haga el barrido de a en un cierto intervalo, y llame a Gmsh y a FeenoX para los casos i y ii:

#!/bin/bash

b="100"   # ancho adimensional del slab
if [ -z $1 ]; then
  n="10"    # número de elementos
else
  n=$1
fi

rm -rf two-zone-slab-*-${n}.dat

# barremos a (posición de la interfaz)
for a in $(seq 35 57); do
  cat << EOF > ab.geo
a = ${a};
b = ${b};
n = ${n};
lc = b/n;
EOF
  for p in i ii; do
    gmsh -1 -v 0 two-zone-slab-${p}.geo
    feenox two-zone-slab.fee ${p} | tee -a two-zone-slab-${p}-${n}.dat
  done
done

Estamos entonces en condiciones de ejecutar este script para poder graficar los errores de ambos métodos:

$ ./two-zone-slab.sh 10
35      1.19332 1.19768 -0.00435617
35      1.18588 1.19768 -0.0117998
36      1.18882 1.19333 -0.0045144
[...]
56      1.0477  1.06819 -0.0204869
57      1.05031 1.05931 -0.00899971
57      1.04029 1.05931 -0.0190241
$ ./two-zone-slab.sh 20
35      1.19647 1.19768 -0.00120766
35      1.19647 1.19768 -0.00120766
36      1.19208 1.19333 -0.00125124
[...]
56      1.06328 1.06819 -0.00490434
57      1.05725 1.05931 -0.00206549
57      1.05303 1.05931 -0.00628299
$

La figura 5.38 ilustra cabalmente el punto de Richard Stallman: en lugar de lidiar con cómo corregir el efecto “cúspide” (por ejemplo modificando la posición de la barra de control artificialmente para reducirlo) es mucho más efectivo evitarlo en primer lugar.

5.7 Estudios paramétricos: el reactor cubo-esferoidal

TL;DR: Un “experimento pensado” para verificar que una esfera es más eficiente que un cubo. No es posible resolver una geometría con bordes curvos con una malla cartesiana estructurada, mientras que elementos curvos de segundo orden pueden discretizar superficies cónicas exactamente.

Todos sabemos que, a volumen constante, un reactor desnudo esférico tiene un factor de multiplicación efectivo mayor que un reactor cúbico (figura 5.39). De hecho a un grupo de energía con aproximación de difusión podemos calcular explícitamente dicho k_\text{eff}.

Pero, ¿qué pasa a medida que el cubo se va transformando en una esfera? Es decir, ¿cómo cambia k_\text{eff} a medida que redondeamos los bordes del cubo como en la figura 5.40? Trabajo para Gmsh & FeenoX. Comencemos con el archivo de entrada de FeenoX, que es realmente sencillo:

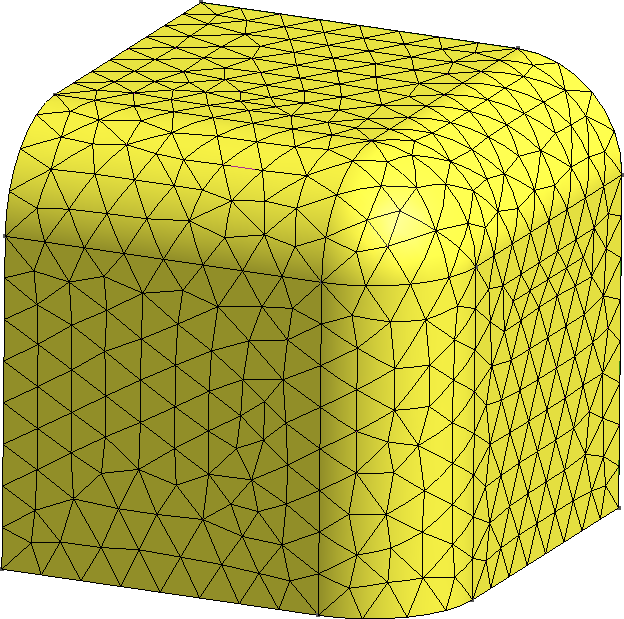
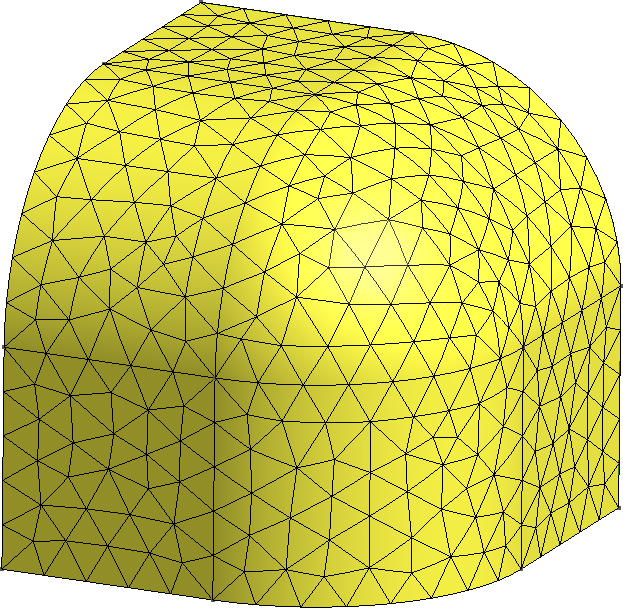
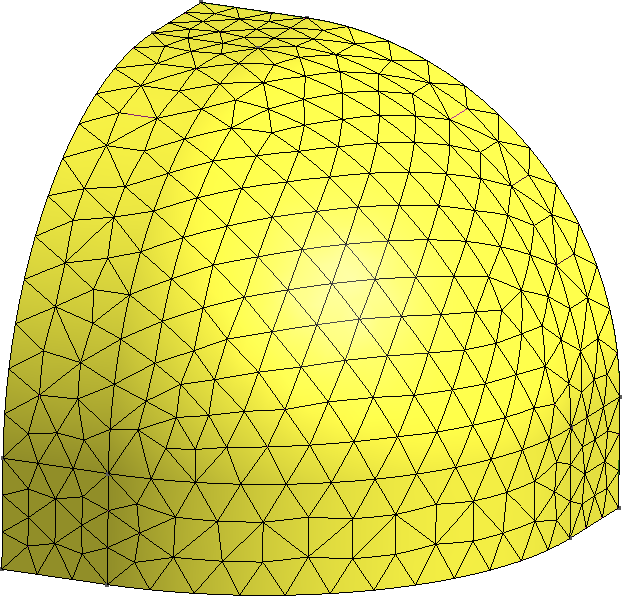
PROBLEM neutron_diffusion DIMENSIONS 3
READ_MESH cubesphere-$1.msh DIMENSIONS 3

D1 = 1.03453E+00
Sigma_a1 = 5.59352E-03
nuSigma_f1 = 6.68462E-03
Sigma_s1.1 = 3.94389E-01

PHYSICAL_GROUP fuel DIM 3
BC internal    mirror
BC external    vacuum

SOLVE_PROBLEM

PRINT HEADER $1 keff 1e5*(keff-1)/keff fuel_volume

En efecto, la mayor complejidad está en generar la malla para una fracción 0 < f < 1 de “esfericidad” (de forma que f=0 sea un cubo y f=1 sea una esfera) para un volumen V constante. Dado que hay cuestiones no triviales, como por ejemplo el hecho de que el kernel geométrico OpenCASCADE no permite hacer una operación tipo “fillet” de forma tal que se eliminen las caras planas originales (que es justamente lo que sucede para f=1) es mejor generar la malla usando la interfaz Python de Gmsh en lugar de un archivo de entrada:

import os
import math
import gmsh

def create_mesh(vol, f100):
  gmsh.initialize()
  gmsh.option.setNumber("General.Terminal", 0)  
  
  f = 0.01*f100
  # cuánto tiene que valer a para mantener el volumen constante?
  a = (vol / (1/8*4/3*math.pi*f**3 + 3*1/4*math.pi*f**2*(1-f) + 3*f*(1-f)**2 + (1-f)**3))**(1.0/3.0)
  
  internal = []
  gmsh.model.add("cubesphere")
  if (f100 < 1):
    # a cube
    gmsh.model.occ.addBox(0, 0, 0, a, a, a, 1)
    internal = [1,3,5]
    external = [2,4,6]

  elif (f100 > 99):
    # a sphere
    gmsh.model.occ.addSphere(0, 0, 0, a, 1, 0, math.pi/2, math.pi/2)
    internal = [2,3,4]
    external = [1]
    
  else:
    gmsh.model.occ.addBox(0, 0, 0, a, a, a, 1)
    gmsh.model.occ.fillet([1], [12, 7, 6], [f*a], True)
    internal = [1,4,6]
    external = [2,3,5,7,8,9,10]

  gmsh.model.occ.synchronize()

  gmsh.model.addPhysicalGroup(3, [1], 1)  
  gmsh.model.setPhysicalName(3, 1, "fuel")
  gmsh.model.addPhysicalGroup(2, internal, 2)  
  gmsh.model.setPhysicalName(2, 2, "internal")
  gmsh.model.addPhysicalGroup(2, external, 3)  
  gmsh.model.setPhysicalName(2, 3, "external")
  
  gmsh.option.setNumber("Mesh.ElementOrder", 2)
  gmsh.option.setNumber("Mesh.Optimize", 1)
  gmsh.option.setNumber("Mesh.OptimizeNetgen", 1)
  gmsh.option.setNumber("Mesh.HighOrderOptimize", 1)
  gmsh.option.setNumber("Mesh.CharacteristicLengthMin", a/10);
  gmsh.option.setNumber("Mesh.CharacteristicLengthMax", a/10);
  
  gmsh.model.mesh.generate(3)
  gmsh.write("cubesphere-%g.msh"%(f))  
  gmsh.finalize()
  return


for f100 in range(0,101,5):
  create_mesh(100**3, f100)
  os.system("feenox cubesphere.fee %g"%(f100))

Al ejecutar directamente este script de Python tenemos el k_\text{eff} en función de f (la última columna muestra el volumen de la malla para verificar que estamos manteniéndolo razonablemente constante para todos los valores de f) que graficamos en la figura 5.41:

$ python cubesphere.py | tee cubesphere.dat 
0       1.05626 5326.13 1e+06
5       1.05638 5337.54 999980
10      1.05675 5370.58 999980
15      1.05734 5423.19 999992
20      1.05812 5492.93 999995
25      1.05906 5576.95 999995
30      1.06013 5672.15 999996
35      1.06129 5775.31 999997
40      1.06251 5883.41 999998
45      1.06376 5993.39 999998
50      1.06499 6102.55 999998
55      1.06619 6208.37 999998
60      1.06733 6308.65 999998
65      1.06839 6401.41 999999
70      1.06935 6485.03 999998
75      1.07018 6557.96 999998
80      1.07088 6618.95 999998
85      1.07143 6666.98 999999
90      1.07183 6701.24 999999
95      1.07206 6721.33 999998
100     1.07213 6727.64 999999
$

Figura 5.41: Reactividad estática vs. fracción de esfericidad f

5.8 Optimización: el problema de los pescaditos

TL;DR: Estudios paramétricos y de optimización al estilo Unix.

Los tres problemas de esta sección—inventados para escribir el artículo [27]—ilustran cómo generalizar las facilidades que provee FeenoX para realizar estudios paramétricos (tal como ya hemos hecho en casi todos los problemas anteriores) para dar un paso más allá y resolver un problema de optimización. Para eso comenzamos resolviendo numéricamente “el problema del pescadito⁹”, que es un clásico en la teoría de perturbaciones lineales. Agregamos luego un segundo pescadito que nada en forma diametralmente opuesta al primero donde mostramos cómo aparecen los dos efectos de apantallamiento y anti-apantallamiento según las posiciones relativas de ambos pescaditos. Pasamos finalmente a dejar dos pescaditos fijos y resolver la pregunta: ¿dónde tenemos que poner un tercer pescadito para que la reactividad neta sea mínima?

Observación. El problema “tradicional” de los pescaditos en tri-dimensional. En esta sección nos quedamos con la versión en dos dimensiones para simplificar el tratamiento—especialmente en la Sección 5.8.3—pero el espíritu es el mismo.

Observación. En los dos primeros problemas podríamos explotar la simetría para reducir el tamaño del problema pero preferimos resolver la geometría completa para ilustrar mejor el problema. Ya hemos discutido la reducción del número total de grados de libertad en la Sección 5.3.

5.8.1 Un pescadito: teoría de perturbaciones lineales

Consideremos un reactor bi-dimensional circular de radio A con centro en el origen del plano x-y y con secciones eficaces macroscópicas homogéneas a un grupo de energías. Supongamos que un pescadito circular absorbente de radio a puede moverse a lo largo del eje x positivo. Un ejercicio clásico de análisis de reactores es dar la reactividad negativa introducida por el pescadito en función de la posición x = r de su centro utilizando teoría de perturbaciones (es decir, suponiendo que a \ll A.

Un pescadito de radio a nada a lo largo del eje x en un reactor homogéneo de radio A.

En esta sección vamos a obtener con FeenoX la reactividad neta introducida por el pescadito variando paramétricamente la posición r \in [0:A-a] de su centro x=r, y=0. Para eso, comenzamos con un script de Bash que…

genera un archivo de texto vars.geo (que es incluido desde un-pescadito.geo para ubicar el círculo pequeño correspondiente al pescadito),
crea una malla no estructurada con Gmsh (figura 5.42)
resuelve la ecuación de difusión con FeenoX para diferentes posiciones r del pescadito.

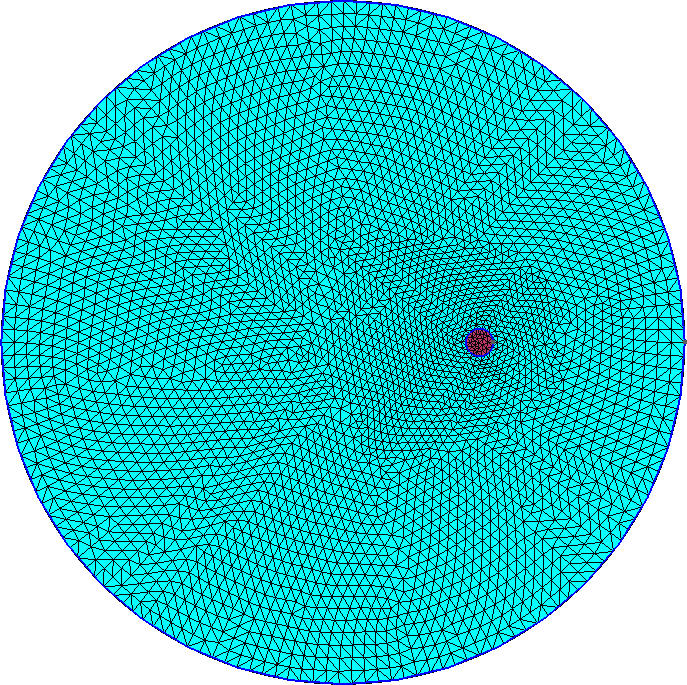
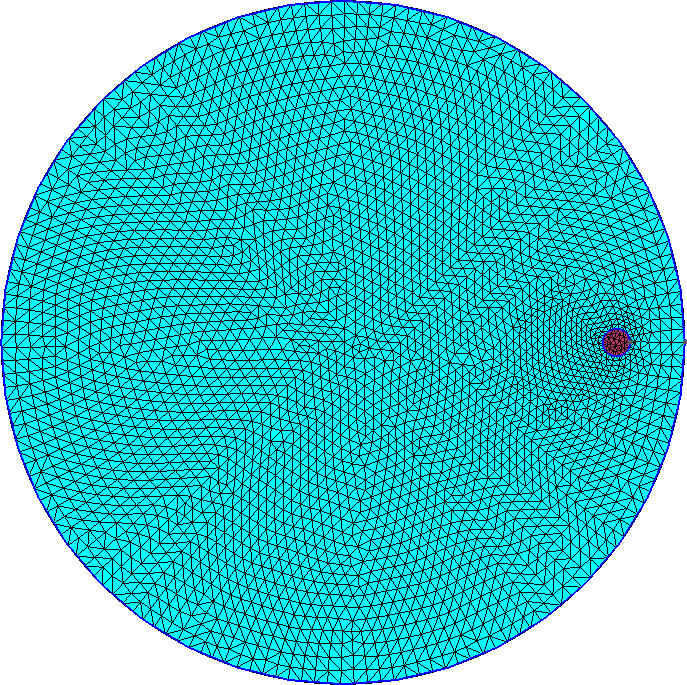
#!/bin/bash

A=50   # radio del reactor
a=2    # radio del pescadito

rm -f tmp
for r in $(feenox steps.fee 0 47 64); do
 cat << EOF > vars.geo 
A = ${A};
a = ${a};
r = ${r};
EOF
 gmsh -2 -v 0 un-pescadito.geo
 feenox un-pescadito.fee | tee -a tmp
done
sort -g tmp > un-pescadito.csv

Observación. Notar que a diferencia de los estudios paramétricos realizados hasta el momento que involucraban una serie creciente de valores, en este caso el bucle for de Bash se realiza sobre la salida del archivo de FeenoX steps.fee:

# steps.fee: genera secuencias de números
DEFAULT_ARGUMENT_VALUE 1 0   # min
DEFAULT_ARGUMENT_VALUE 2 1   # max
DEFAULT_ARGUMENT_VALUE 3 1   # steps
DEFAULT_ARGUMENT_VALUE 4 0   # offset
static_steps = $4+$3
x = quasi_random($1,$2)
IF (step_static>($4+0.1))
 PRINT x
ENDIF

que genera una sucesión (determinística) de números cuasi-aleatorios que, eventualmente, llena densamente un hipercubo [22]. En los lazos paramétricos crecientes, si se desea aumentar la densidad del barrido hay que volver a calcular todo el intervalo nuevamente. En una serie de números cuasi-aleatorios, es posible agregar nuevos puntos a los ya calculados dando un offset inicial. En la Sección 5.11 esta característica de las serie cuasi-aleatorias es más evidente ya que allí barremos densamente un espacio de parámetro bi-dimensional. Por ejemplo, podemos barrer el intervalo [0,1] con tres puntos con el archivo steps.fee como

$ feenox steps.fee 0 1 3
0.5
0.75
0.25
$

Si luego del estudio quisiéramos agregar cuatro puntos más, comenzamos con el offset 3 para obtener

$ feenox steps.fee 0 1 4 3
0.375
0.875
0.625
0.125
$

El archivo de entrada de Gmsh genera dos círculos y asigna etiquetas para materiales y condiciones de contorno:

Merge "vars.geo";

SetFactory("OpenCASCADE");
Disk(1) = {0, 0, 0, A};
Disk(2) = {r, 0, 0, a};
Coherence;

Physical Curve("external") = {1};
Physical Surface("fuel") = {3};
Physical Surface("pescadito") = {2};

Color Cyan      { Surface{3}; }
Color Maroon    { Surface{2}; }

Mesh.Algorithm = 9;
Mesh.MeshSizeMax = A/25;
Mesh.MeshSizeFromCurvature = 16;
Mesh.Optimize = 1;

El archivo de entrada de FeenoX es muy sencillo:

PROBLEM neutron_diffusion GROUPS 1 DIMENSIONS 2
READ_MESH un-pescadito.msh
INCLUDE xs.fee
INCLUDE vars.geo
SOLVE_PROBLEM

# calculamos la reactividad que tendría el círculo sin pescaditos
# para eso miramos las XS en un punto donde sepamos que no va a estar el pescadito
rho0 = (nuSigma_f1(0.5*A,0.5*A) - Sigma_a1(0.5*A,0.5*A) - D1(0.5*A,0.5*A)*(2.4048/A)^2)/nuSigma_f1(0.5*A,0.5*A)
rho = (keff-1)/keff

# el delta rho que metió el pescado vs. r
PRINT r 1e5*(rho-rho0)

La única “complejidad” aparece al calcular el incremento negativo de reactividad con respecto al k_\text{eff} analítico del círculo original. Para ello ponemos una condición de contorno de flujo nulo en la circunferencia dentro del archivo incluido xs.fee:

# secciones eficaces
MATERIAL fuel       D1=1   Sigma_a1=0.02  nuSigma_f1=0.03
MATERIAL pescadito  D1=0.9 Sigma_a1=0.10
BC external null

Observación. La constante 2.4048 que aparece en el archivo de entrada de FeenoX es una aproximación del primer cero de la función J_0(\xi) de Bessel.

Al ejecutar el script obtenemos la curva que mostramos en la figura 5.43: mientras más alejado del centro nade el pescadito, menor es la reactividad neta introducida.

$ ./un-pescadito.sh 
23.5    -606.765
35.25   -202.255
11.75   -1094.41
[...]
24.2344 -576.9
0.734375        -1339.52
1.10156 -1338.06
$

Figura 5.43: Curva “S” de reactividad negativa introducida por un pescadito en un reactor circular.

5.8.2 Dos pescaditos: estudio paramétrico no lineal

Figura 5.44: Dos pescaditos de radio a nadan a lo largo del eje x en forma diametralmente opuesta.

Agreguemos ahora otro pescadito nadando en forma diametralmente opuesta al primero (figura 5.44). El script de Bash, el archivo de entrada de Gmsh y el de FeenoX son muy similares a los de la sección anterior por lo que no los mostramos. Ahora al graficar la curva de reactividad en función de r y compararla con el doble de la reactividad introducida por un único pescadito calculada en la sección anterior (figura 5.45 (a)) vemos los dos efectos explicados en el capítulo 14 de la referencia clásica [10] (figura 5.45 (b)). Si los pescaditos están lejos entre sí sus reactividades negativas son más efectivas porque se anti-apantallan. Pero al acercarse, se apantallan y la reactividad neta es menor que por separado.

(a) Reactividad debida a dos pescaditos y el doble de la reactividad de uno solo.

5.8.3 Tres pescaditos: optimización

Supongamos ahora que agregamos un tercer pescadito. Por alguna razón, los primeros dos pescaditos están fijos en dos posiciones arbitrarias [x_1,y_1] y [x_2,y_2]. Tenemos que poner el tercer pescadito en una posición [x_3,y_3] de forma tal de hacer que la reactividad total sea lo menor posible.¹⁰

Una forma de resolver este problema con FeenoX es atacarlo en forma similar a la manera en que procedimos que en las secciones anteriores. Pero ahora en lugar de variar la posición del tercer pescadito en forma paramétrica según una receta determinística ya conocida de antemano, utilizar un algoritmo de optimización que decida la nueva posición del tercer pescadito en función de la historia de posiciones y los valores de reactividad calculados por FeenoX en cada paso.

Observación. En la reciente tesis de maestría [36] se emplea FeenoX para resolver la ecuación de calor y, mediante un script en Python, optimizar topológicamente el reflector de un reactor nuclear integrado. Esa tesis, junto con esta sección, ayuda a ilustrar el punto que queremos enfatizar sobre la flexibilidad en el diseño de FeenoX para ser utilizada como una herramienta de optimización.

En particular, podemos usar la biblioteca de Python SciPy que provee acceso a algoritmos de optimización y permite con muy pocas líneas de Python implementar el bucle de optimización:

#!/usr/bin/python
from scipy.optimize import minimize 
import numpy as np
import subprocess

def keff(x3):
  r = subprocess.run(["bash", "tres.sh", "(%s)" % str(x3[0]), "(%s)" % str(x3[1])], stdout=subprocess.PIPE)
  k = float(r.stdout.decode('utf-8'))
  return k

x3_0 = [+25, -25]
result = minimize(keff, x3_0, method="nelder-mead")
print(result)

Observación. En forma deliberada hemos mostrado en este caso un driver script muy sencillo para mostrar que realmente es posible realizar un cálculo de optimización con muy poco código extra. Sin embargo, el esquema propuesto también funciona para otros algoritmos de optimización más complejos como recocido simulado, algoritmos genéticos o incluso aquellos basados en redes neuronales.

La función keff() a optimizar es función de la posición \mathbf{x}_3 del tercer pescadito, cuyas dos componentes son pasadas como argumento al script de Bash que llama primero a Gmsh y luego a FeenoX para devolver el k_\text{eff}(\mathbf{x}_3) para \mathbf{x}_1 y \mathbf{x}_2 fijos:

cat << EOF > x3.geo 
x3 = $1;
y3 = $2;
EOF
gmsh -2 -v 0 tres-pescaditos.geo
feenox tres-pescaditos.fee

Merge "vars.geo";

x1 = -10;    // centro del pescado 1
y1 = 5;

x2 = 25;     // centro del pescado 2
y2 = -15;

Merge "x3.geo";

SetFactory("OpenCASCADE");
Disk(1) = {0, 0, 0, A};
Disk(2) = {x1, y1, 0, a};
Disk(3) = {x2, y2, 0, a};
Disk(4) = {x3, y3, 0, a};
Coherence;

Physical Curve("external") = {1};
Physical Surface("fuel") = {5};
Physical Surface("pescadito") = {2,3,4};

Color Cyan      { Surface{5}; }
Color Maroon    { Surface{2,3,4}; }

Mesh.Algorithm = 9;
Mesh.MeshSizeMax = A/25;
Mesh.MeshSizeFromCurvature = 16;
Mesh.Optimize = 1;

PROBLEM neutron_diffusion 2D
READ_MESH tres-pescaditos.msh
INCLUDE xs.fee
SOLVE_PROBLEM

PRINT %.8f keff

Observación. Si FeenoX, tal como Gmsh, tuviese una interfaz Python (tarea que está planificada e incluso tenida en cuenta en la base de diseño de FeenoX) entonces la función keff(x3) a minimizar sería más elegante que la propuesta, que involucra hacer un fork()+exec() para invocar a un script de Bash que hace otros dos fork()+exec() para ejecutar gmsh y feenox.

La ejecución del script de optimización muestra la reactividad mínima en fun y la posición óptima del tercer pescadito en x. Podemos ver los pasos intermedios en la figura 5.46 y 5.47.

$ ./tres.py 
 final_simplex: (array([[ 3.55380249, -1.15953827],
       [ 3.41708565, -1.71419764],
       [ 3.89513397, -1.83193016]]), array([1.29409226, 1.29409476, 1.294099  ]))
           fun: 1.29409226
       message: 'Optimization terminated successfully.'
          nfev: 37
           nit: 20
        status: 0
       success: True
             x: array([ 3.55380249, -1.15953827])
$

Figura 5.46: Pasos intermedios del problema de optimización de los tres pescaditos resuelto con el algoritmo de Nelder-Mead [12].

5.9 Verificación con el método de soluciones fabricadas

TL;DR: Para verificar los algoritmos numéricos de un código con el método de soluciones fabricadas se necesita que dicho código permita definir propiedades materiales en función del espacio a través de expresiones algebraicas arbitrarias.

Como mencionamos brevemente en la Sección 5.5, la verificación de códigos de cálculo involucra mostrar que dicho código resuelve correctamente las ecuaciones que debe resolver. La forma de hacerlo es calcular alguna medida del error cometido por el método numérico implementado en el código, por ejemplo el error L_2

e_2 = \frac{\displaystyle \sqrt{ \int \Big[ \phi_\text{num}(\mathbf{x}) - \phi_\text{ref}(\mathbf{x}) \Big]^2 \, d^D \mathbf{x}]}}{\displaystyle \int d^D \mathbf{x}} \tag{5.2}

y mostrar que dicho error tiende a cero cuando el tamaño del problema discretizado tiene a infinito. Según la referencia [20],

“The code author defines precisely what continuum partial differential equations and continuum boundary conditions are being solved, and convincingly demonstrates that they are solved correctly, i.e., usually with some order of accuracy, and always consistently, so that as some measure of discretization (e.g. the mesh increments), the code produces a solution to the continuum equations; this is Verification.”

Más aún, según la referencia [21] dice

… we recommend that, when possible, one should demonstrate that the equations are solved to the theoretical order-of-accuracy of the discretization method.

Esto quiere decir que la forma de tender a cero debe coincidir con el orden predicho por la teoría. Para difusión de neutrones con elementos finitos, este orden es 2 para elementos de primer orden y 3 para elementos de segundo orden. La forma de hacer esto es

Resolver el problema para un cierto tamaño característico h de malla.
Calcular el error e_2 (o alguna otra medida del error) en función de h.
Verificar que la pendiente de e_2 vs. h en un gráfico log-log es la predicha por la teoría.

De todas maneras, para mostrar que el error tiende a cero necesitamos tener una expresión algebraica para la solución exacta de la ecuación que queremos resolver. Es decir, necesitamos conocer \phi_\text{ref}(\mathbf{x}) en la ecuación 5.2. Está claro que si conociéramos esta expresión para un caso general, esta tesis no tendría razón de ser. Y es razonable que no exista esta expresión porque, de alguna manera, resolver la ecuación de difusión de neutrones involucra “integrar” dos veces la fuente de neutrones.

El método de soluciones fabricadas (o MMS por sus siglas en inglés) propone recorrer el camino inverso: partir de una solución conocida (es decir, fabricada ad hoc) y preguntarnos cuál es la fuente necesaria para dar lugar a ese flujo. Este camino es mucho más sencillo ya que involucra “derivar” la fuente dos veces, y es el método que ilustramos en esta sección.

Por otro lado, [21] también dice que hay que asegurarse “probar” todas las características del software, incluyendo

condiciones de contorno
tipos de elementos
solvers algebraicos
modelos de materiales
etc.

lo que rápidamente da lugar a una explosión combinatoria de parámetros como la que apareció en la Sección 5.4. Siguen diciendo los autores de [21]

To ensure that all code options relevant to code Verification are tested, one must design a suite of coverage tests. Fortunately, this is not as daunting as it may seem at first. If a code has options, the number of coverage tests needed to verify the code is determined by the number of mutually exclusive options, i.e., there is no combinatorial explosion of tests to run. For example, suppose a code has two solver options and three constitutive relationship (CR) options. Then only three coverage tests are needed to check all options. Test (1): Solver 1 with CR1, Test (2): Solver 2 with CR2,Test (3): Solver 1 or 2 with CR3. One does not need to perform a test involving the combination, for example, Solver 1 and CR2 because Test 1 will ascertain whether of not Solver 1 is working correctly, while Test 2 will ascertain whether or not CR2 is working correctly.

En mi experiencia personal, la explosión combinatoria sí existe. La aplicación de este método al problema de conducción de calor es objeto de estudio de un informe técnico [28] y una presentación a un congreso [29]. En las dos secciones que siguen lo aplicamos al problema de difusión de neutrones, primero a un grupo con secciones eficaces uniformes en tres dimensiones para introducir la idea. Luego en la Sección 5.9.2 a dos grupos con secciones eficaces dependientes del espacio en dos dimensiones.

Observación. Para verificar un código con el método de MMS es condición necesaria que el código permita definir fuentes a través de expresiones algebraicas. Es también recomendable que permita realizar estudios paramétricos con cierta facilidad y automatización razonable [30].

5.9.1 Stanford bunny a un grupo

Consideremos un reactor con la forma del conejo de Stanford (figura 5.48) con secciones eficaces adimensionales uniformes D=1 y \Sigma_a=0.05. La ecuación de difusión es entonces

Figura 5.48: El famoso y nunca bien ponderado conejo de Stanford

-\text{div} \left[ D \cdot \text{grad}(\phi) \right] + \Sigma_a \cdot \phi(x,y,z) = S(x,y,z) \tag{5.3}

Propongamos una solución fabricada para el flujo escalar, digamos

\phi(x,y,z) = \log\left[ 1 + 10^{-2} \cdot z \cdot (y+50)\right] + 10 \cdot ( x + \sqrt{y+50}) \tag{5.4}

La fuente que necesitamos proviene de reemplazar la ecuación 5.4 en la ecuación 5.3. Siguiendo las reglas de generación y de composición de Unix lo que hacemos es usar Maxima, que es un sistema para la manipulación simbólica y numérica de expresiones libre, abierto y ameno a la filosofía Unix, para que haga las cuentas por nosotros. En efecto, consideremos el siguiente archivo de entrada:

phi1_mms(x,y,z) = log(1+1e-2*z*(y+50)) + 1e-3*(x+sqrt(y+50))
D1(x,y,z) = 1
Sigma_a1(x,y,z) = 0.05

DEFAULT_ARGUMENT_VALUE 1 tet4      # elemento = tet4/tet10
DEFAULT_ARGUMENT_VALUE 2 16        # factor de refinamiento
DEFAULT_ARGUMENT_VALUE 3 0         # escribimos vtk? = 0/1

READ_MESH bunny-$1-$2.msh
PROBLEM neutron_diffusion 3D

# incluimos la fuente calculada con maxima
INCLUDE neutron-bunny-s.fee

# ponemos condicion de contorno de dirichlet
BC external phi1=phi1_mms(x,y,z)

SOLVE_PROBLEM

# salidas
PHYSICAL_GROUP bunny DIM 3
h = (bunny_volume/cells)^(1/3)

# L-2 error
INTEGRATE (phi1(x,y,z)-phi1_mms(x,y,z))^2 RESULT e_2
error_2 = sqrt(e_2)/bunny_volume

# L-inf error
FIND_EXTREMA abs(phi1(x,y,z)-phi1_mms(x,y,z)) MAX error_inf

PRINT %.6f log(h) log(error_inf) log(error_2) %g $2 cells nodes %.2f 1024*memory() wall_time()

IF $3
  WRITE_MESH neutron-bunny_$1-$2-$3.vtk phi1 phi1_mms phi1(x,y,z)-phi1_mms(x,y,z)
ENDIF

De hecho, dado que la sintaxis del parser algebraico de Maxima es (casi) la misma que la de FeenoX, podemos tomar la cadena con la solución fabricada del archivo de entrada de FeenoX, calcular la fuente con Maxima y generar un archivo válido de FeenoX que podemos incluir desde el archivo de entrada principal:

# primero leemos el flujo y las XSs del input de FeenoX
phi1_mms=$(grep "phi1_mms(x,y,z) =" neutron-bunny.fee | sed 's/=/:=/')
D1=$(grep "D1(x,y,z) =" neutron-bunny.fee | sed 's/=/:=/')
Sigma_a1=$(grep "Sigma_a1(x,y,z) =" neutron-bunny.fee | sed 's/=/:=/')

# y después le pedimos a maxima que haga las cuentas por nosotros
maxima --very-quiet << EOF > /dev/null
${phi1_mms};
${D1};
${Sigma_a1};
s1(x,y,z) := -(diff(D1(x,y,z) * diff(phi1_mms(x,y,z), x), x) + diff(D1(x,y,z) * diff(phi1_mms(x,y,z), y), y) + diff(D1(x,y,z) * diff(phi1_mms(x,y,z), z), z)) + Sigma_a1(x,y,z)*phi1_mms(x,y,z);
stringout("neutron-bunny-s1.txt", s1(x,y,z));
tex(s1(x,y,z), "neutron-bunny-s1.tex");
EOF

No sólo le pedimos a Maxima que nos genere el archivo de entrada de FeenoX sino que también le podemos pedir que nos dé los macros TeX [9] para documentar la fuente en esta tesis:

\begin{aligned} S(x,y,z) =& 0.05\,\left(\log \left(0.01\,\left(y+50\right)\,z+1\right) + 0.001\, \left(\sqrt{y+50}+ x\right)\right)\\ & +{{1.0 \times 10^{-4}\,z^2}\over{ \left(0.01\,\left(y+50\right)\,z+1\right)^2}} +{{1.0 \times 10^{-4}\, \left(y+50\right)^2}\over{\left(0.01\,\left(y+50\right)\,z+1\right)^ 2}} +{{2.5 \times 10^{-4}}\over{\left(y+50\right)^{{{3}\over{2}}}}} \end{aligned}

Lo siguiente es completar el script de Bash para generar las mallas apropiadas y graficar los resultados automáticamente:

$ ./run.sh 
# manufactured solution (input)
phi1_mms(x,y,z) := log(1+1e-2*z*(y+50)) + 1e-3*(x+sqrt(y+50));
D1(x,y,z) := 1;
Sigma_a1(x,y,z) := 0.05;

# source term (output)
S1(x,y,z) = 0.05*(log(0.01*(y+50)*z+1)+0.001*(sqrt(y+50)+x))+(1.0E-4*z^2)/(0.01*(y+50)*z+1)^2+(1.0E-4*(y+50)^2)/(0.01*(y+50)*z+1)^2+2.5E-4/(y+50)^(3/2)
neutron_bunny_tet4
--------------------------------------------------------
0.882892        -2.913390       -11.628276      20      19682   4707    83.33   1.81
0.713751        -3.078327       -11.919410      24      32742   7373    92.86   2.49
0.566854        -3.515901       -12.236276      28      50921   10955   108.16  2.81
0.324435        -2.603344       -12.683721      36      105483  21355   146.90  5.16
0.224405        -3.864497       -12.850835      40      142438  28201   172.97  6.03
0.131075        -2.897239       -13.077100      44      188504  36661   204.51  7.86
0.045617        -2.848969       -13.264638      48      243633  46614   248.88  10.02
-0.068898       -3.793360       -13.505172      54      343580  64510   320.61  14.57
-0.172894       -3.198078       -13.685647      60      469441  86726   402.82  21.13
-0.236015       -3.197992       -13.823714      64      567349  103924  472.32  25.57
neutron_bunny_tet10
--------------------------------------------------------
1.089532        -4.742025       -13.429947      16      10558   17898   100.68  1.16
0.882892        -3.691744       -14.159585      20      19682   31819   132.57  1.80
0.713751        -5.421880       -14.599096      24      32742   51285   169.52  3.20
0.566854        -5.350408       -15.058052      28      50921   77891   223.38  3.79
0.439039        -6.402456       -15.381134      32      74757   112362  304.81  4.98
0.324435        -4.280207       -15.699625      36      105483  156399  393.84  7.43
0.224405        -5.660364       -15.980139      40      142438  208860  509.98  10.78
0.131075        -3.946231       -16.107267      44      188504  273940  646.90  13.82
0.045617        -3.738939       -16.333378      48      243633  351128  807.37  18.35
$ pyxplot neutron-bunny.ppl
$

Observación. Aún para mallas relativamente gruesas como la de la figura 5.49, la diferencia entre el flujo numérico y la solución manufacturada es muy pequeña para ser observada a simple vista. Es necesario calcular la integral de los errores y ajustar el orden de convergencia para realmente verificar el código.

Figura 5.50: Error e_2 vs. tamaño del elemento h para el conejo de Stanford

La figura 5.50 ilustra por qué el tamaño del elemento h no es una buena medida de la precisión de una discretización: obviamente, para un mismo tamaño de celda, la precisión obtenida por los elementos de mayor orden es, justamente, mucho mayor. Es por eso que es más apropiado hablar de la cantidad total de incógnitas, de grados de libertad o tamaño del problema.

5.9.2 Cuadrado a dos grupos

Simplifiquemos un poco la geometría para poder introducir complejidades en la matemática. Tomemos como geometría el cuadrado [0:1] \times [0:1], pero estudiemos el problema a dos grupos con el siguiente juego de secciones eficaces:

phi1_mms(x,y) = 1 + sin(2*x)^2 * cos(3*y)^2
D1(x,y) = 1 + 0.1*(x - 0.5*y)
Sigma_a1(x,y) = 1e-3*(1 + log(1+x) - 0.5*y^3)
Sigma_s1_2(x,y) = 1e-3*(1 - x + sqrt(0.5*y))

phi2_mms(x,y) = (1-0.5*tanh(-y))*log(1+x)
D2(x,y) = 1
Sigma_a2(x,y) = 1e-3
Sigma_s2_1(x,y) = 0

Como ahora la geometría es más sencilla, además de fijar solamente condiciones de Dirichlet en los cuatro lados del cuadrado vamos a poner dos condiciones de Dirichlet y dos de Neumann. Necesitamos entonces—además de las dos fuentes volumétricas S1(x,y) y S2(x,y)—que Maxima nos calcule las dos componentes de las dos corrientes para que las podamos usar como condiciones de contorno:

phi1_mms=$(grep "phi1_mms(x,y) =" neutron-square.fee | sed 's/=/:=/')
phi2_mms=$(grep "phi2_mms(x,y) =" neutron-square.fee | sed 's/=/:=/')

D1=$(grep "D1(x,y) =" neutron-square.fee | sed 's/=/:=/')
Sigma_a1=$(grep "Sigma_a1(x,y) =" neutron-square.fee | sed 's/=/:=/')
Sigma_s1_2=$(grep "Sigma_s1_2(x,y) =" neutron-square.fee | sed 's/=/:=/')

D2=$(grep "D2(x,y) =" neutron-square.fee | sed 's/=/:=/')
Sigma_a2=$(grep "Sigma_a2(x,y) =" neutron-square.fee | sed 's/=/:=/')
Sigma_s2_1=$(grep "Sigma_s2_1(x,y) =" neutron-square.fee | sed 's/=/:=/')

maxima --very-quiet << EOF > /dev/null
${phi1_mms};
${phi2_mms};
${D1};
${Sigma_a1};
${Sigma_s1_2};
${D2};
${Sigma_a2};
${Sigma_s2_1};
s1(x,y) := -(diff(D1(x,y) * diff(phi1_mms(x,y), x), x) + diff(D1(x,y) * diff(phi1_mms(x,y), y), y)) + Sigma_a1(x,y)*phi1_mms(x,y) - Sigma_s2_1(x,y)*phi2_mms(x,y);
s2(x,y) := -(diff(D2(x,y) * diff(phi2_mms(x,y), x), x) + diff(D2(x,y) * diff(phi2_mms(x,y), y), y)) + Sigma_a2(x,y)*phi2_mms(x,y) - Sigma_s1_2(x,y)*phi1_mms(x,y);
stringout("neutron-square-s1.txt", s1(x,y));
stringout("neutron-square-s2.txt", s2(x,y));
stringout("neutron-square-j1x.txt", -D1(x,y) * diff(phi1_mms(x,y),x));
stringout("neutron-square-j1y.txt", -D1(x,y) * diff(phi1_mms(x,y),y));
stringout("neutron-square-j2x.txt", -D2(x,y) * diff(phi2_mms(x,y),x));
stringout("neutron-square-j2y.txt", -D2(x,y) * diff(phi2_mms(x,y),y));
EOF

El archivo de entrada de FeenoX continúa de la siguiente manera

READ_MESH square-$2-$3-$4.msh DIMENSIONS 2
PROBLEM neutron_diffusion GROUPS 2

DEFAULT_ARGUMENT_VALUE 1 dirichlet # BCs = dirichlet/neumann
DEFAULT_ARGUMENT_VALUE 2 tri3      # shape = tri3/tri6/quad4/quad8/quad9
DEFAULT_ARGUMENT_VALUE 3 struct    # algorithm = struct/frontal/delaunay
DEFAULT_ARGUMENT_VALUE 4 8         # refinement factor = 1/2/3/4...
DEFAULT_ARGUMENT_VALUE 5 0         # write vtk? = 0/1

# read the results of the symbolic derivatives
INCLUDE neutron-square-s.fee

# set the BCs (depending on $1)
INCLUDE neutron-square-bc-$1.fee

SOLVE_PROBLEM   # this line should be self-explanatory

para terminar calculando el error e_2 (y el error e_\infty que ni siquiera discutimos por falta de espacio-tiempo) en forma similar al caso del conejo.

Los dos archivos con condiciones de contorno son el ya conocido 100% Dirichlet:

BC left   phi1=phi1_mms(x,y)    phi2=phi2_mms(x,y)
BC right  phi1=phi1_mms(x,y)    phi2=phi2_mms(x,y)
BC bottom phi1=phi1_mms(x,y)    phi2=phi2_mms(x,y)
BC top    phi1=phi1_mms(x,y)    phi2=phi2_mms(x,y)

y el nuevo caso 50% Dirichlet 50% Neumann, donde en los lados bottom y right ponemos el producto interno de la corriente \mathbf{J}_g(\mathbf{x}) con la normal exterior \hat{\mathbf{n}}(\mathbf{x}):

BC left   phi1=phi1_mms(x,y)    phi2=phi2_mms(x,y)
BC top    phi1=phi1_mms(x,y)    phi2=phi2_mms(x,y)
BC bottom J1=+Jy1_mms(x,y)      J2=+Jy2_mms(x,y)
BC right  J1=-Jx1_mms(x,y)      J2=-Jx2_mms(x,y)

Como ahora nuestra geometría es más sencilla podemos utilizar algoritmos de mallado estructurados. Incluso podemos estudiar qué sucede si usamos triángulos y cuadrángulos, de primer y segundo orden y completos (quad8) o incompletos (quad9), como someramente ilustramos en la figura 5.51. Con los dos tipos de condiciones de contorno, que podrían ser muchas más combinaciones de porcentajes de Dirichlet y Neumann. ¡Bienvenida la explosión combinatoria!

El resto del trabajo consiste en

ejecutar el script de Bash,
dejar que Maxima haga la manipulación simbólica, y
obtener con FeenoX los resultados de la figura 5.52.

La siguiente mímica de terminal ilustra la ejecución a través del script run.sh:

$ ./run.sh 
# manufactured solution (input)
phi1_mms(x,y) := 1 + sin(2*x)^2 * cos(3*y)^2;
phi2_mms(x,y) := (1-0.5*tanh(-y))*log(1+x);
D1(x,y) := 1 + 0.1*(x - 0.5*y);
Sigma_a1(x,y) := 1e-3*(1 + log(1+x) - 0.5*y^3);
Sigma_s1_2(x,y) := 1e-3*(1 - x + sqrt(0.5*y));
D2(x,y) := 1;
Sigma_a2(x,y) := 1e-3;
Sigma_s2_1(x,y) := 0;

# source terms (output)
S1(x,y) = (-18*sin(2*x)^2*(0.1*(x-0.5*y)+1)*sin(3*y)^2)-0.3*sin(2*x)^2*cos(3*y)*sin(3*y)+0.001*((-0.5*y^3)+log(x+1)+1)*(sin(2*x)^2*cos(3*y)^2+1)+26*sin(2*x)^2*(0.1*(x-0.5*y)+1)*cos(3*y)^2-8*cos(2*x)^2*(0.1*(x-0.5*y)+1)*cos(3*y)^2-0.4*cos(2*x)*sin(2*x)*cos(3*y)^2
S2(x,y) = (-0.001*(0.7071067811865476*sqrt(y)-x+1)*(sin(2*x)^2*cos(3*y)^2+1))+1.0*log(x+1)*sech(y)^2*tanh(y)+0.001*log(x+1)*(0.5*tanh(y)+1)+(0.5*tanh(y)+1)/(x+1)^2
J1x(x,y) = 4*cos(2*x)*sin(2*x)*((-0.1*(x-0.5*y))-1)*cos(3*y)^2
J1y(x,y) = -6*sin(2*x)^2*((-0.1*(x-0.5*y))-1)*cos(3*y)*sin(3*y)
J2x(x,y) = -(0.5*tanh(y)+1)/(x+1)
J2y(x,y) = -0.5*log(x+1)*sech(y)^2
neutron_square_dirichlet_tri3_struct
--------------------------------------------------------
-1.732868	-1.940256	-2.857245	4	32	25	68.38	0.85
-1.956012	-2.294614	-3.245481	6	50	36	68.60	1.48
-2.426015	-3.135938	-4.117575	8	128	81	68.32	1.11
[...]
-2.079442	-6.417214	-7.519575	8	64	225	68.92	1.04
-2.302585	-6.909677	-8.086373	10	100	341	67.30	0.68
neutron_square_neumann_quad8_frontal
--------------------------------------------------------
-1.545521	-4.303977	-5.509111	4	22	83	66.53	1.30
-1.903331	-5.471960	-6.794112	6	45	160	70.89	0.92
-2.191013	-6.055953	-7.497523	8	80	273	69.48	1.55
-2.393746	-6.834924	-8.197128	10	120	401	69.51	1.19
$

Observación. La expresión para la componente y de la corriente de grupo 2 involucra una secante hiperbólica—que proviene de la derivada de una tangente hiperbólica—que FeenoX puede evaluar sin inconvenientes como una de las funciones internas, tales como log(), exp(), sin(), cos(), atan(), atan2(), random(), etc.

Figura 5.52: Error e_2 vs. tamaño del elemento h para el cuadrado a dos grupos

5.10 PHWR de siete canales y tres barras de control inclinadas

TL;DR: Mallas no estructuradas, dependencias espaciales no triviales, escalabilidad en paralelo. Si el problema no “entra” en una computadora, lo podemos repartir entre varias.

En esta última sección del capítulo resolvemos un problema 100% inventado, desde la geometría (figura 5.53) hasta las secciones eficaces. La geometría es adimensional “tipo” PHWR con siete canales verticales dentro de un tanque moderador y tres barras de control inclinadas.

Observación. La tesis de doctorado [16] trata sobre el modelado de barras de control inclinadas, incluyendo cálculo a nivel de celda y a nivel de núcleo. En el nivel de celda se tiene en cuenta la geometría continua para calcular secciones eficaces macroscópicas. Pero luego estas secciones eficaces son usadas a nivel de núcleo en una malla estructurada obteniendo los mismos dibujos tipo “Lego” que mostramos en la figura 1.7 de la Sección 1.2. Este problema propone tener en cuenta la inclinación de las barras en el cálculo de núcleo. Queda como trabajo futuro el análisis de la forma correcta de generar las secciones eficaces con cálculo a nivel de celda para garantizar la consistencia del esquema de cálculo multi-escala (Sección 2.5).

Luego, en esta sección las secciones eficaces son, tal como la geometría, 100% inventadas. Más aún, para el moderador, el invento incluye una dependencia con un perfil (lineal) de la temperatura del moderador en función de la coordenada vertical:

Tmod0 = 100
Tmod(z) = 100 + (200-100)*(z/400)
FUNCTION sigmat_mod(T) INTERPOLATION linear DATA {
90  0.108
100 0.112
110 0.116
130 0.118
180 0.120
200 0.122 }

MATERIAL moderator {
  Sigma_t1=0.068
  Sigma_t2=sigmat_mod(Tmod(z))
  Sigma_s1.1=0.06+1e-5*(Tmod(z)-Tmod0)
  Sigma_s1.2=0.002
  Sigma_s2.1=0
  Sigma_s2.2=sigmat_mod(Tmod(z))-0.005
  nuSigma_f1=0
  nuSigma_f2=0
}

Observación. De acuerdo con la idea de evitar complejidad innecesaria, las secciones eficaces de los canales combustibles son uniformes. Pero en una aplicación real, éstas deberían depender de…

el quemado
la concentración de venenos
la temperatura del combustible
la temperatura del refrigerante
la densidad del refrigerante

Todas estas dependencias se pueden dar en forma similar a la dependencia de las XS del moderador con una mezcla de expresiones algebraicas (Sección 4.2) e interpolación de funciones dadas por puntos de una o más variables (Sección 4.3). Incluso se pueden diseñar esquemas de acople con códigos externos e intercambiar información a través de memoria compartida [33], [35] o de mensajes MPI.

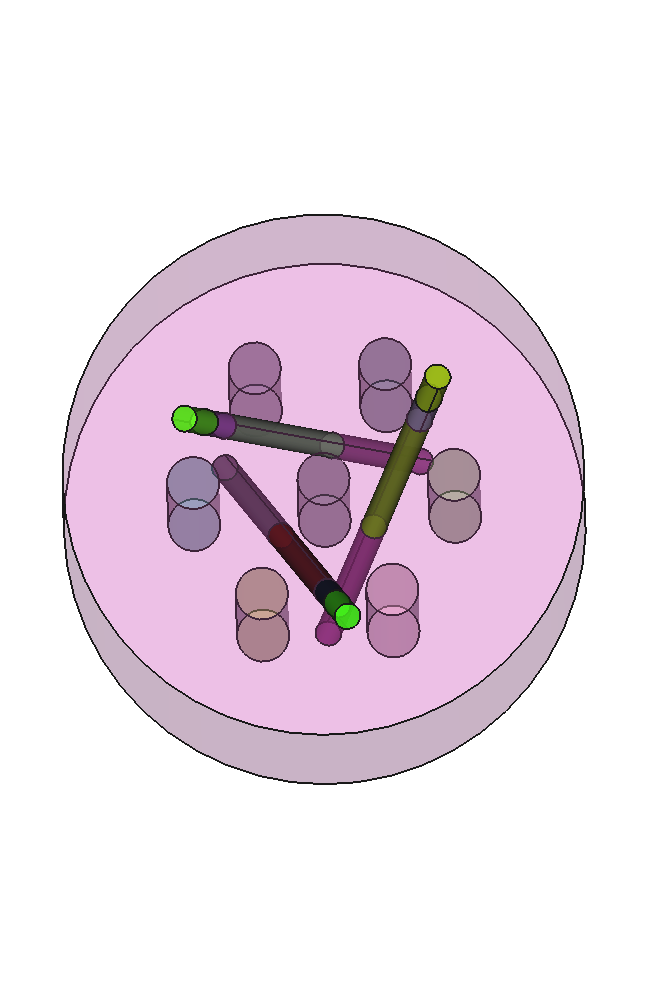
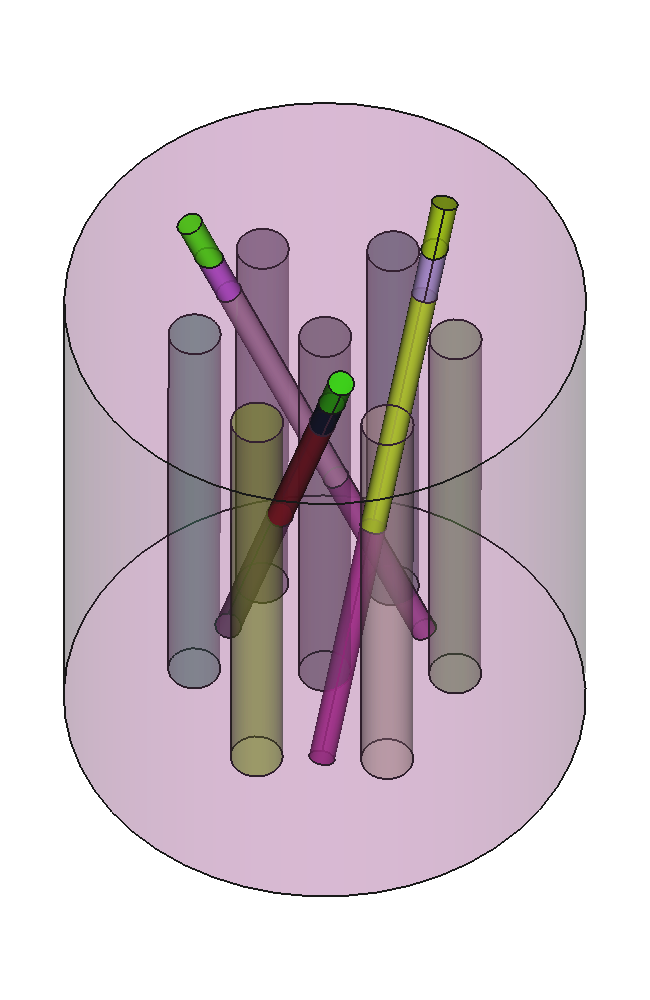
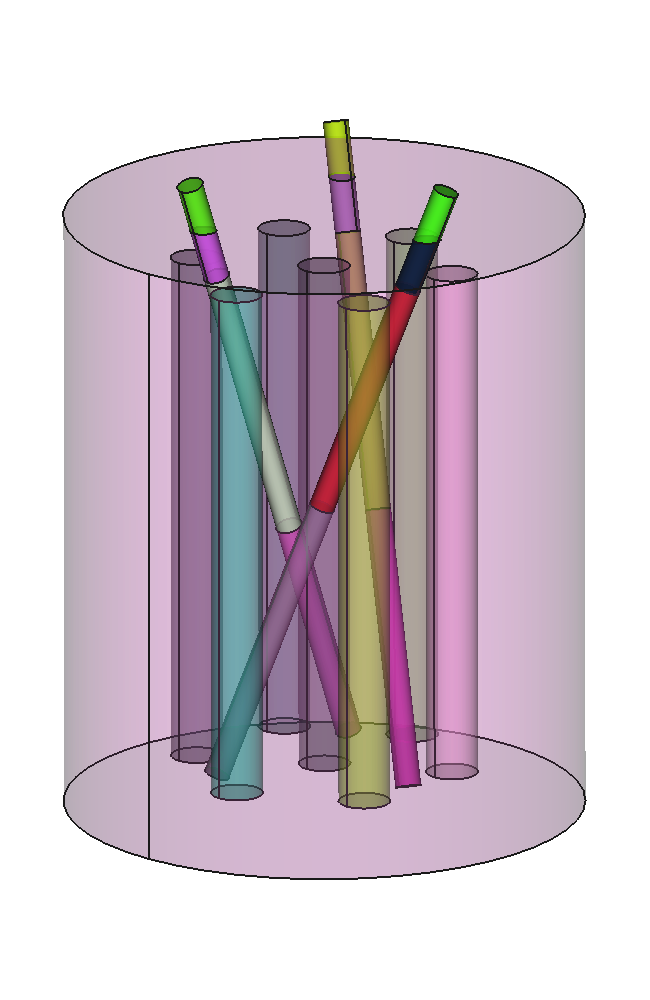
5.10.1 Difusión con elementos de segundo orden

Resolvemos primero las ecuaciones de difusión a dos grupos sobre una malla con elementos curvos tipo tet10 (figura 5.54). El archivo de entrada de FeenoX, una vez que separamos la secciones eficaces (y hemos puesto toda la complejidad en la geometría y en la malla) es extremadamente sencillo:

PROBLEM neutron_diffusion 3D GROUPS 2 PRECONDITIONER mumps
READ_MESH phwr2.msh INTEGRATION reduced
INCLUDE xs.fee
SOLVE_PROBLEM

WRITE_RESULTS FORMAT vtk

mem_global = mpi_memory_global()
PRINTF     "size = %g\ttime = %.1f s\t memory = %.1f Gb" total_dofs wall_time() mem_global
PRINTF_ALL "local memory = %.1f Gb" mpi_memory_local()

A dos grupos, la malla de segundo orden resulta en poco más de 250 mil grados de libertad. Veamos cómo escala FeenoX en términos de tiempo y memoria al resolver este problema con diferente cantidad de procesadores en una misma computadora:

$ for i in 1 2 4 8 12; do mpirun -n $i feenox phwr-dif.fee; done
size = 256964   time = 94.6 s    memory = 6.5 Gb
[0/1 tux] local memory = 6.5 Gb
size = 256964   time = 61.5 s    memory = 7.9 Gb
[0/2 tux] local memory = 4.2 Gb
[1/2 tux] local memory = 3.7 Gb
size = 256964   time = 49.7 s    memory = 9.5 Gb
[0/4 tux] local memory = 2.3 Gb
[1/4 tux] local memory = 2.4 Gb
[2/4 tux] local memory = 2.4 Gb
[3/4 tux] local memory = 2.4 Gb
size = 256964   time = 46.2 s    memory = 12.9 Gb
[0/8 tux] local memory = 1.6 Gb
[1/8 tux] local memory = 1.6 Gb
[2/8 tux] local memory = 1.9 Gb
[3/8 tux] local memory = 1.5 Gb
[4/8 tux] local memory = 1.6 Gb
[5/8 tux] local memory = 1.5 Gb
[6/8 tux] local memory = 1.5 Gb
[7/8 tux] local memory = 1.7 Gb
size = 256964   time = 48.8 s    memory = 15.1 Gb
[0/12 tux] local memory = 1.3 Gb
[1/12 tux] local memory = 1.2 Gb
[2/12 tux] local memory = 1.1 Gb
[3/12 tux] local memory = 1.4 Gb
[4/12 tux] local memory = 1.5 Gb
[5/12 tux] local memory = 1.2 Gb
[6/12 tux] local memory = 1.1 Gb
[7/12 tux] local memory = 1.1 Gb
[8/12 tux] local memory = 1.2 Gb
[9/12 tux] local memory = 1.0 Gb
[10/12 tux] local memory = 1.6 Gb
[11/12 tux] local memory = 1.4 Gb
$

Si bien el tiempo de pared disminuye, no lo hace tanto como debería ya que todavía hay mucho lugar para optimización en FeenoX, especialmente en paralelización por MPI. Pero podemos observar que el comportamiento es esencialmente el esperado. Más importante aún es el comportamiento de la memoria: a medida que usamos más procesos (o “ranks” en terminología de MPI), la memoria requerida en cada uno disminuye sensiblemente. Esto implica que FeenoX puede—en principio—resolver problemas arbitrariamente grandes si se dispone de suficientes computadoras que puedan ser interconectadas por MPI, que era una de las premisas de esta tesis.¹¹ La figura 5.55 muestra la distribución de flujos rápido y térmico resultantes.

5.10.2 Ordenadas discretas con elementos de primer orden

Resolvamos ahora el mismo problema pero con ordenadas discretas. Comenzamos por S_2, que involucra ocho direcciones por cada grupo de energías. Para tener un tamaño de problema comparable utilizamos tetraedros de primer orden. Estudiemos cómo cambia el tiempo de pared y la memoria con 1, 2, 4 y 8 procesos MPI:

$ for i in 1 2 4 8; do mpirun -n $i feenox phwr-s2.fee; done
size = 257920   time = 409.7 s   memory = 20.1 Gb
[0/1 tux] local memory = 20.1 Gb
size = 257920   time = 286.3 s   memory = 25.5 Gb
[0/2 tux] local memory = 11.5 Gb
[1/2 tux] local memory = 14.1 Gb
size = 257920   time = 289.3 s   memory = 29.5 Gb
[0/4 tux] local memory = 7.6 Gb
[1/4 tux] local memory = 6.8 Gb
[2/4 tux] local memory = 7.2 Gb
[3/4 tux] local memory = 8.0 Gb
size = 257920   time = 182.7 s   memory = 33.9 Gb
[0/8 tux] local memory = 4.5 Gb
[1/8 tux] local memory = 4.4 Gb
[2/8 tux] local memory = 4.4 Gb
[3/8 tux] local memory = 4.6 Gb
[4/8 tux] local memory = 4.3 Gb
[5/8 tux] local memory = 4.1 Gb
[6/8 tux] local memory = 3.7 Gb
[7/8 tux] local memory = 4.0 Gb
$

Figura 5.56: Disminución de la memoria por proceso MPI

Resolver un problema formulado en S_N es computacionalmente mucho más demandante porque las matrices resultantes no son simétricas y tienen una estructura compleja. Los requerimientos de memoria y CPU son mayores que para difusión. Incluso la escala de paralelización, aún cuando debemos notar nuevamente que hay mucho terreno para mejorar en FeenoX, es peor que en la sección anterior para un tamaño de problema similar. El esfuerzo necesario es más marcado mientras mayor sea N. De hecho para una malla más gruesa todavía, dando lugar a un tamaño de problema menor, obtenemos:

$ mpiexec -n 1 feenox phwr-s4.fee
size = 159168   time = 390.1 s   memory = 20.0 Gb
[0/1 tux] local memory = 20.0 Gb
$ mpiexec -n 2 feenox phwr-s4.fee
size = 159168   time = 297.6 s   memory = 25.0 Gb
[0/2 tux] local memory = 12.5 Gb
[1/2 tux] local memory = 12.5 Gb
$ mpiexec -n 4 feenox phwr-s4.fee
size = 159168   time = 276.7 s   memory = 27.5 Gb
[0/4 tux] local memory = 7.7 Gb
[1/4 tux] local memory = 6.9 Gb
[2/4 tux] local memory = 6.2 Gb
[3/4 tux] local memory = 6.6 Gb
$ mpiexec -n 8 feenox phwr-s4.fee
size = 159168   time = 153.3 s   memory = 33.7 Gb
[0/8 tux] local memory = 5.0 Gb
[1/8 tux] local memory = 4.7 Gb
[2/8 tux] local memory = 3.2 Gb
[3/8 tux] local memory = 3.5 Gb
[4/8 tux] local memory = 3.5 Gb
[5/8 tux] local memory = 4.8 Gb
[6/8 tux] local memory = 4.8 Gb
[7/8 tux] local memory = 4.3 Gb
$

Esto es, para el mismo número de grados de libertad totales el tiempo y memoria necesario para resolver el problema con S_4 aumenta. De todas maneras, lo que sí sigue siendo cierto, como mostramos en la figura 5.56, es que a medida que aumentamos la cantidad de procesos de MPI la memoria local disminuye.

Para finalizar, debemos notar que al resolver problemas de criticidad lo que FeenoX hace es transformar la formulación numérica desarrollada en el capítulo 3 en un problema de auto-valores y auto-vectores generalizado como explicamos en la Sección 3.5.3. Para resolver este tipo de problemas se necesita un solver lineal que pueda “invertir”¹² la matriz de fisiones. Los algoritmos para resolver problemas de autovalores provistos en la biblioteca SLEPc funcionan significativamente mejor si este solver lineal es directo. Es conocido que los solvers directos son robustos pero no son escalables. Por lo tanto, los problemas resueltos con FeenoX (usando las opciones por defecto) suelen ser robustos pero no escalan bien (de hecho en la Sección 5.3.5 hemos resuelto un problema de criticidad con un solver lineal usando opciones en la línea de comandos). Es por eso también que los problemas sin fuentes independientes son más intensivos computacionalmente que los problemas con fuentes, que pueden ser resueltos como un sistema de ecuaciones lineales (o eventualmente no lineales con un esquema tipo Newton-Raphson).

(a)
Formulación	DOFs	Problema	Build	Solve	Total	Mem.
Difusión	257k	KSP	3.5 s	5.4 s	10.6 s	0.6 Gb
		EPS	6.9 s	66.3 s	74.7 s	6.4 Gb
S_2	258k	KSP	30.4 s	228.1 s	260.0 s	17.7 Gb
		EPS	63.2 s	368.6 s	432.9 s	19.8 Gb
S_4	159k	KSP	64.7 s	449.1 s	514.6 s	23.3 Gb
		EPS	138.9 s	598.8 s	738.3 s	27.0 Gb

Tabla 5.6: Tiempos necesarios para construir y resolver diferentes formulaciones para casos con fuentes (KSP) o de criticidad (EPS)

En efecto, como vemos en la tabla 5.6, en el caso de difusión con fuentes independientes, la matriz de rigidez es simétrica y el operador es elíptico. Esto hace que sea muy eficiente usar un pre-condicionador geométrico-algebraico multi-grilla (GAMG) combinado con un solver de Krylov tipo gradientes conjugados, tanto en términos de CPU como de memoria. Justamente esa combinación es el default para problemas tipo neutron_diffusion en FeenoX. Por otro lado, al resolver neutron_sn, aún para problemas con fuente se necesita un solver directo ya que de otra manera la convergencia es muy lenta con un impacto directo en la cantidad de memoria necesaria.

Observación. En la Sección 5.9 hemos verificado solamente la primera fila de la tabla 5.6.

5.11 Bonus track: cinética puntual*

TL;DR: Ilustración del hecho de que FeenoX puede resolver ecuaciones diferenciales ordinarias además de en derivadas parciales.

Además de ecuaciones en derivadas parciales, FeenoX puede resolver sistemas de ecuaciones diferenciales ordinarias y de ecuaciones algebraicas-diferenciales. En esta sección extra ilustramos rápidamente las funcionalidades, aplicadas a las ecuaciones de cinética puntual de reactores. Todos los casos usan los siguientes parámetros cinéticos, definido en un archivo parameters.fee e incluido en los inputs de cada una de las secciones que siguen:

nprec = 6    # seis grupos de precursores
VECTOR c[nprec]
VECTOR lambda[nprec] DATA 0.0124   0.0305   0.111    0.301    1.14     3.01
VECTOR beta[nprec]   DATA 0.000215 0.001424 0.001274 0.002568 0.000748 0.000273
Beta = vecsum(beta)
Lambda = 40e-6

5.11.1 Cinética puntual directa con reactividad vs. tiempo

Este primer ejemplo resuelve cinética puntual con una reactividad \rho(t) dada por una “tabla”,¹³ es decir, una función de un único argumento (el tiempo t) definida por pares de puntos [t,\rho(t)] e interpolada linealmente:

INCLUDE parameters.fee   # parámetros cinéticos
PHASE_SPACE phi c rho    # espacio de fases
end_time = 100           # tiempo final

rho_0 = 0                # condiciones iniciales
phi_0 = 1
c_0[i] = phi_0 * beta[i]/(Lambda*lambda[i])

# "tabla" de reactividad vs. tiempo en pcm
FUNCTION react(t) DATA {   0    0 
                           5    0
                           10  10
                           30  10
                           35   0
                           100  0   }

# sistema de DAEs
rho = 1e-5*react(t)
phi_dot = (rho-Beta)/Lambda * phi + vecdot(lambda, c)
c_dot[i] = beta[i]/Lambda * phi - lambda[i]*c[i]

PRINT t phi rho    # salida: phi y rho vs. tiempo

La figura 5.57 muestra el nivel de flujo \phi(t) y la reactividad \rho(t) tal como la utilizó FeenoX para resolver el sistema dinámico definido con la palabra clave PHASE_SPACE (que es un sustantivo).

Figura 5.57: Flujo y reactividad directa

5.11.2 Cinética inversa

Ahora tomamos la salida \phi(t) del caso anterior y resolvemos cinética inversa de dos maneras diferentes:

Con la fórmula integral de la literatura clásica [5]

INCLUDE parameters.fee
FUNCTION flux(t) FILE flux.dat

# definimos una función de flujo que permite tiempos negativos
flux_a = vec_flux_t[1]
flux_b = vec_flux_t[vecsize(vec_flux)]
phi(t) = if(t<flux_a, flux(flux_a), flux(t))

# calculamos la reactividad con la fórmula integral
VAR t'
rho(t) := { Lambda * derivative(log(phi(t')),t',t) +
  Beta * ( 1 - 1/phi(t) *
   integral(phi(t-t') * sum((lambda[i]*beta[i]/Beta)*exp(-lambda[i]*t'), i, 1, nprec), t', 0, 1e4) ) }

PRINT_FUNCTION rho MIN 0 MAX 50 STEP 0.1

Resolviendo el mismo sistema de DAEs pero leyendo \phi(t) en lugar de \rho(t)

INCLUDE parameters.fee
PHASE_SPACE phi c rho

end_time = 50
dae_rtol = 1e-7

rho_0 = 0
phi_0 = 1
c_0[i] = phi_0 * beta[i]/(Lambda*lambda[i])

FUNCTION flux(t) FILE flux.dat

phi = flux(t)
phi_dot = (rho-Beta)/Lambda * phi + vecdot(lambda, c)
c_dot[i] = beta[i]/Lambda * phi - lambda[i]*c[i]

PRINT t phi rho

Obtenemos entonces la figura 5.58. El caso 2 es “adaptativo” en el sentido de que dependiendo del error tolerado y de las derivadas temporales de las variables del espacio de las fases en función de t, el esfuerzo computacional se adapta automáticamente a través del paso de tiempo \Delta t con el que se resuelve el sistema DAE. Por defecto, el método es Adams-Bashforth de orden variable (implementado por la biblioteca SUNDIALS [6]), donde justamente el orden de integración se ajusta dinámicamente también dependiendo del error.

5.11.3 Control de inestabilidades de xenón

Ahora introducimos un poco más de complejidad. A las ecuaciones de cinética puntual le agregamos cinética de xenón 135. Como el sistema dinámico resultante es Lyapunov-inestable¹⁴ ante cambios de flujo, la reactividad es ahora una función de la posición de una barra de control ficticia cuya importancia está dada por una interpolación tipo Steffen de su posición adimensional z. Una lógica de control PI (con una banda muerta del 0.3%) “mueve” dicha barra de control de forma tal de forzar al reactor a bajar la potencia del 100% al 80% en mil segundos, mantenerse durante tres mil segundos a esa potencia y volver al 100% en cinco mil:

INCLUDE parameters.fee
FUNCTION setpoint(t) DATA {
0     1
1000  1
2000  0.8
5000  0.8
10000 1
20000 1 }

end_time = vecmax(vec_setpoint_t)  # tiempo final = último tiempo de setpoint(t)
max_dt = 1                         # no dejamos que dt aumente demasiado

# importancia de la barra de control como función de la inserción
FUNCTION rodworth(z) INTERPOLATION akima DATA {
0     2.155529e+01*1e-5*10
0.2   6.337352e+00*1e-5*10    
0.4  -3.253021e+01*1e-5*10
0.6  -7.418505e+01*1e-5*10   
0.8  -1.103352e+02*1e-5*10   
1    -1.285819e+02*1e-5*10  }

# constantes para el xenón
gammaX = 1.4563E10       # xenon-135 direct fission yield
gammaI = 1.629235E11     # iodine-135 direction fission yield
GammaX = -3.724869E-17   # xenon-135 reactivity coefficiente
lambdaX = 2.09607E-05    # xenon-135 decay constant
lambdaI = 2.83097E-05    # iodine-135 decay constant
sigmaX = 2.203206E-04    # microscopic XS of neutron absorption for Xe-134

PHASE_SPACE rho phi c I X
INITIAL_CONDITIONS_MODE FROM_VARIABLES

z_0 = 0.5                # estado estacionario
phi_0 = 1
c_0[i] = phi_0 * beta[i]/(Lambda*lambda[i])
I_0 = gammaI*phi_0/lambdaI
X_0 = (gammaX + gammaI)/(lambdaX + sigmaX*phi_0) * phi_0
rho_bias_0 = -rodworth(z_0) - GammaX*X_0

# --- DAEs ------------------------------
rho = rho_bias + rodworth(z) + GammaX*X
phi_dot = (rho-Beta)/Lambda * phi + vecdot(lambda, c)
c_dot[i] = beta[i]/Lambda * phi - lambda[i]*c[i]
I_dot = gammaI * phi - lambdaI * I
X_dot = gammaX * phi + lambdaI * I - lambdaX * X - sigmaX * phi * X

# --- sistema de control ----------------
# movemos la barra de control si el error excede una banda muerta del 0.3%
vrod = 1/500    # 1/500-avos de núcleo por segundo
band = 3e-3
error = phi - setpoint(t)
z = z_0 + integral_dt(vrod*((error>(+band))-(error<(-band))))

PRINT t phi z setpoint(t)

La figura 5.59 muestra el flujo y la posición de la barra de control. Se puede observar que la dinámica no es trivial, pero puede ser modelada en forma relativamente sencilla con FeenoX.

Figura 5.59: Flujo y posición de la barra de control en un caso con xenón bajo control

5.11.4 Mapas de diseño

Finalizamos recuperando unos resultados derivados de mi tesis de maestría [24] publicados en 2010 [31]. Consiste en cinética puntual de un reactor de investigación con retroalimentación termohidráulica por temperatura del refrigerante y del combustible escrita como modelos de capacitancia concentrada¹⁵ cero-dimensionales. El estudio consiste en barrer paramétricamente el espacio de coeficientes de reactividad [\alpha_c, \alpha_f], perturbar el estado del sistema dinámico (\Delta T_f = 2~\text{ºC}) y marcar con un color la potencia luego de un minuto para obtener mapas de estabilidad tipo Lyapunov.

nprec = 6    # six precursor groups
VECTOR c[nprec]
VECTOR lambda[nprec] DATA 1.2400E-02 3.0500E-02 1.1100E-01 3.0100E-01 1.1400E+00 3.0100E+00 
VECTOR beta[nprec]   DATA 2.4090e-04 1.5987E-03 1.4308E-03 2.8835E-03 8.3950E-04 3.0660E-04
Beta = vecsum(beta)
Lambda = 1.76e-4

IF in_static
 alpha_T_fuel = 100e-5*(qrng2d_reversehalton(1,$1)-0.5)
 alpha_T_cool = 100e-5*(qrng2d_reversehalton(2,$1)-0.5)

 Delta_T_cool = 2
 Delta_T_fuel = 0

 P_star = 18.8e6       # watts
 T_in = 37             # grados C 
 hA_core = 1.17e6      # watt/grado
 mc_fuel = 47.7e3      # joule/grado
 mc_cool = 147e3       # joule/grado
 mflow_cool = 520      # kg/seg
 c_cool = 4.18e3 * 147e3/mc_cool       # joule/kg
ENDIF

PHASE_SPACE phi c T_cool T_fuel rho
end_time = 60
dae_rtol = 1e-7

rho_0 = 0
phi_0 = 1
c_0[i] = phi_0 * beta(i)/(Lambda*lambda(i))

T_cool_star = 1/(2*mflow_cool*c_cool) * (P_star+2*mflow_cool*c_cool*T_in)
T_fuel_star = 1/(hA_core) * (P_star + hA_core*T_cool_star)

T_cool_0 = T_cool_star + Delta_T_cool
T_fuel_0 = T_fuel_star + Delta_T_fuel
INITIAL_CONDITIONS_MODE FROM_VARIABLES

rho = 0
phi_dot = (rho + alpha_T_fuel*(T_fuel-T_fuel_star) + alpha_T_cool*(T_cool-T_cool_star) - Beta)/Lambda * phi + vecdot(lambda, c)
c_dot[i] = beta[i]/Lambda * phi - lambda[i]*c[i]
T_fuel_dot = (1.0/(mc_fuel))*(P_star*phi - hA_core*(T_fuel-T_cool))
T_cool_dot = (1.0/(mc_cool))*(hA_core*(T_fuel-T_cool) - 2*mflow_cool*c_cool*(T_cool-T_in))

done = done | (phi > 4)

IF done
 PRINT alpha_T_fuel alpha_T_cool phi
ENDIF

Para barrer el espacio de parámetros usamos series de números cuasi-aleatorios [8] de forma tal de poder realizar ejecuciones sucesivas que van llenando densamente dicho espacio como ilustramos en la figura 5.60 (a):

for i in $(seq $1 $2); do  feenox point.fee $i | tee -a point.dat; done

$ ./point.sh 0 2048
$ ./point.sh 2048 4096
$

(a) Estabilidad de Lyapunov utilizando series de números pseudo-aleatorios que van “rellenando” incremental y densamente el espacio de parámetros.

[1]

Ahrens J, Geveci B, Law C, «ParaView: An End-User Tool for Large Data Visualization», en Visualization Handbook, Elesvier, 2005.

[2]

ANS, «Argonne Code Center: Benchmark Problem Book», Argonne National Laboratory, ANL-7416 Supplement 2, jun. 1977.

[3]

Azmy YY, «The Weighted Diamond-Difference Form of Nodal Transport Methods», Nuclear Science and Engineering, vol. 98, n.º 1, pp. 29-40, 1988, doi: 10.13182/NSE88-6.

[4]

Babcsány B, «Development of a finite-element-based reactor physics code system for the solution of the simplified P3 approximation to the neutron transport equation», A thesis submitted for the degree of Doctor of Philosophy, Budapest University of Technology; Economics, 2021.

[5]

Duderstadt JJ, Hamilton LJ, Nuclear Reactor Analysis. Wiley, New York, 1976.

[6]

Gardner DJ, Reynolds DR, Woodward CS, Balos CJ, «Enabling new flexibility in the SUNDIALS suite of nonlinear and differential/algebraic equation solvers», ACM Transactions on Mathematical Software (TOMS), 2022, doi: 10.1145/3539801.

[7]

Geuzaine C, Remacle JF, «Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities», International Journal for Numerical Methods in Engineering, vol. 79, n.º 11, pp. 1309-1331, 2009.

[8]

Halton JH, «Algorithm 247: Radical-Inverse Quasi-Random Point Sequence», Commun. ACM, vol. 7, n.º 12, pp. 701-702, dic. 1964, doi: 10.1145/355588.365104.

[9]

Knuth DE, The TeXbook. Addison-Wesley, 1984.

[10]

Lamarsh JR, Introduction to Nuclear Reactor Theory. Addisson-Wesley, 1966.

[11]

Martin WR, Yehnert CE, Lorence L, Duderstad JJ, «Phase-Space Finite Element Methods Applied To The First-Order Form Of The Transport Equation», Annals of Nuclear Energy, vol. 8, pp. 633-646, 1981.

[12]

Nelder JA, Mead R, «A Simplex Method for Function Minimization», The Computer Journal, vol. 7, n.º 4, pp. 308-313, ene. 1965, doi: 10.1093/comjnl/7.4.308.

[13]

Oberkampf WL, Trucano TG, «Verification and validation benchmarks», Nuclear Engineering and Design, vol. 238, pp. 716-743, 2008, Disponible en: https://api.semanticscholar.org/CorpusID:110737903

[14]

Park HK, «Coupled Space-Angle Adaptivity And Goal-Oriented Error Control For Radiation Transport Calculations», Tesis doctoral, Georgia Institute of Technology, 2006.

[15]

Pellegrino E, «Desarrollo de un código neutrónico de transporte multigrupo 3D por el método de elementos finitos». Proyecto Integrador de la Carrera de Ingeniería Nuclear, Instituto Balseiro, 2010.

[16]

Raouafi H, «Simulation de mécanismes de contrôle de la réactivité inclinés du réacteur SCWR-canadien en utilisant les codes Dragon-5 et Donjon-3», Tesis doctoral, École Polytechnique De Montréal, 2017.

[17]

Raymond ES, The Art of UNIX Programming. Addison-Wesley, 2003.

[18]

Reed WH, «New Difference Schemes for the Neutron Transport Equation», Nuclear Science and Engineering, vol. 46, n.º 2, pp. 309-314, 1971, doi: 10.13182/NSE46-309.

[19]

Ritchie D, Thompson K, «The UNIX time-sharing system», Communications of the ACM, vol. 7, n.º 17, pp. 365-375, 1974, doi: 10.1145/361011.361061.

[20]

Roache PJ, Verification and Validation in Computational Science and Engineering. Albuquerque NM: Hermosa Publishers, 1998.

[21]

Salari K, Knupp P, «Code Verification by the Method of Manufactured Solutions», Sandia Natioal Laboratories, SAMD2000-1444, 2000.

[22]

Sobol IM, «Distribution of points in a cube and approximate evaluation of integrals», U.S.S.R Comput. Maths. Math. Phys., vol. 7, pp. 86-112, 1967.

[23]

Sood A, Forster RA, Parsons DK, «Analytical Benchmark Test Set for Criticality Code Verification», Los Alamos National Laboratory, LA-13511, 1999.

[24]

Theler G, «Análisis no lineal de inestabilidades en el problema acoplado termohidráulico-neutrónico». Tesis de la Carrera de Maestría en Ingeniería, Instituto Balseiro, 2008.

[25]

Theler G, «Difusión de neutrones en mallas no estructuradas: comparación entre volúmenes y elementos finitos». Monografía Final de la materia «Introducción al método de elementos finitos», Universidad de Buenos Aires, 2013.

[26]

Theler G, «Unstructured Grids and the Multigroup Neutron Diffusion Equation», Science and Technology of Nuclear Installations, vol. 2013:641863, 2013, doi: 10.1155/2013/641863.

[27]

Theler G, «Geometric Optimization of Nuclear Reactor Cores», Mecánica Computacional, vol. XXXII, n.º Number 32 Optimization and Control, pp. 2659-2709, 2013.

[28]

Theler G, «Verification by the Method of Manufactured Solutions: application to the steady-state thermal problem», Onscale, 2021.

[29]

Theler G, «Verification of PDE solvers with the Method of Manufactured Solutions», en Ansys TechCon, Pittsburg, 2023.

[30]

Theler G, «Sobre la verificación de un Solver neutrónico con el método de soluciones fabricadas», en 9va. Reunión Anual Grupo Argentino de Cálculo y Análisis de Reactores, 2023.

[31]

Theler G, Bonetto FJ, «On the stability of the point reactor kinetics equations», Nuclear Engineering and Design, vol. 240, n.º 6, pp. 1443-1449, jun. 2010, doi: 10.1016/j.nucengdes.2010.03.007.

[32]

Theler G, Bonetto FJ, Clausse A, «Solution of the 2D IAEA PWR Benchmark with the neutronic code milonga», Actas de la Reunión Anual de la Asociación Argentina de Tecnología Nuclear, vol. XXXVIII, 2011.

[33]

Theler G, Gómez Omil JP, Pellegrino E, «A shared-memory-based coupling scheme for modeling the behavior of a Nuclear Power Plant core», Mecánica Computacional, vol. XXXII, n.º Number 18 Multiphysics, pp. 1501-1517, 2013.

[34]

Van Criekingen S, «Mixed-Hybrid Discretization Methods for the Linear Transport Equation», Tesis doctoral, Northwestern University, 2004.

[35]

Vasconcelos Araújo Silva V, «Acoplamento neutrônico e termo-hidráulico usando os códigos milonga e OpenFOAM: uma abordagem com software livre», Pós-Graduação Em Ciências E Técnicas Nucleares Doutor em Ciências e Técnicas Nucleares, Universidade Federal De Minas Gerais, 2016.

[36]

Winter AEP, «Optimización térmica del reflector de un reactor nuclear», mathesis, Instituto Balseiro, 2023.

Del inglés streams.↩︎
En el sentido del inglés kernel.↩︎
Notar que el hecho de que los argumentos estén disponibles en el input como $1, $2, etc. (o incluso como ${1}, ${2}, etc.) coincide con la sintaxis de Bash, lo que sigue la regla de Unix de sorpresa mínima (Sección C.10).↩︎
El término “comercial” no está siendo usado como oposición a “software libre” o “código abierto”. Como discutimos en la Sección 4.4.1, es éste un error común. Pero de ninguna manera que un software sea comercial implica que no pueda ser libre o abierto. La palabra “comercial” solamente indica que la herramienta con la que comparamos FeenoX forma parte de una biblioteca que se vende comercialmente, hay clientes que pagan por usarla y hay personas que dan soporte técnico a los clientes como un servicio de post-venta.↩︎
El autor de dicho blog está al tanto de la comparación con FeenoX.↩︎
La plataforma CAEplex desarrollada por el autor de esta tesis que provee una interfaz web para una versión anterior de FeenoX corriendo en la nube está 100% integrada en Onshape para realizar cálculos termo-mecánicos.↩︎
Hay un juego de palabras en inglés que indica que verificación quiere decir “are we solving the equations right?” mientras que validación quiere decir “are we solving the right equations?”. En la Sección 5.9 discutimos más en detalle este concepto.↩︎
Del inglés Method of Manufactured Solutions.↩︎
Decidimos usar la palabra pescadito en lugar de pececito ya que es mucho más simpática. Además, es poco probable que un pez pueda sobrevivir nadando en un reactor líquido homogéneo de sales fundidas.↩︎
Reemplazar “pescadito” por “lanza de inyección de boro de emergencia” para pasar de un problema puramente académico a un problema de interés en ingeniería nuclear.↩︎
Quedan como trabajos futuros el análisis de convergencia de otros pre-condicionadores y el estudio de escalabilidad en paralelo de problemas tipo S_N (Sección 6.1}).↩︎
En el sentido de resolver un problema lineal, no de calcular explícitamente la inversa densa de una matriz rala.↩︎
Recordar que uno de los puntos centrales de la filosofía de diseño de FeenoX es evitar el ambiguo y anacrónico concepto de “tabla” en favor de “función definida por puntos”.↩︎
Para observar “oscilaciones de xenón” es necesario a. un lazo de control a lazo cerrado y b. cinética espacial o multi-puntual.↩︎
Del inglés lumped capacitance.↩︎